ABC300

ABC300E

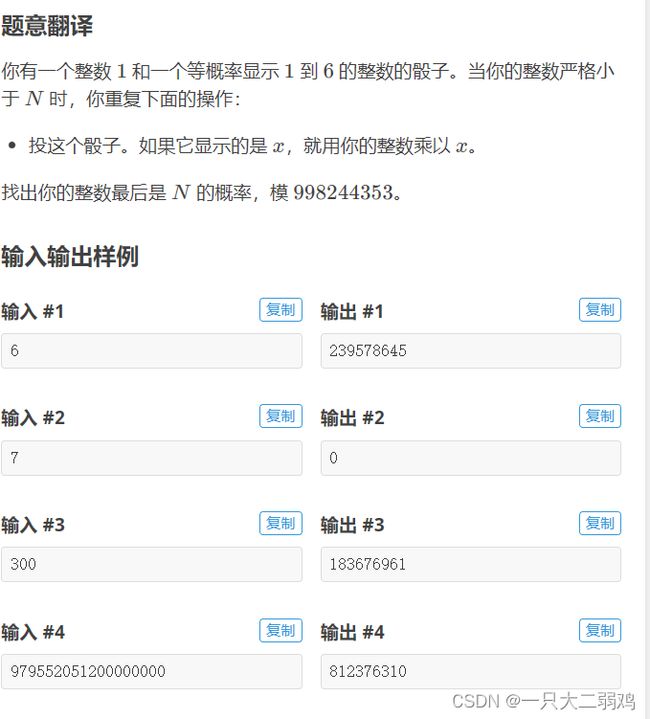
题面

思路

对于投骰子，最后一步可能得到1、2、3、4、5、6，那么对应的最后一步之前的数是n/1、n/2、n/3、n/4、n/5，n/6。并且每个数字（1、2、3、4、5、6）得到的概率是一样的，即为1/6。

也就是F(n)=(1/6)(F(n/1)+F(n/2)+F(n/3)+F(n/4)+F(n/5)+F(n/6))*{只有n%4==0，F(n/4)才能产生贡献，其余同理}

移项得：F(n)=1/5(F(n/1)+F(n/2)+F(n/3)+F(n/4)+F(n/5))，如果一位数组能开下，就可以直接线性dp进行状态转移，但是这个n<=1e18，所以用记忆化搜索的方式实现dp，记录mp[x]为得到x的概率，由于在取模过程中进行了/5操作，所以求一下5在 mod 99824435意义下的乘法逆元即可

细节：mp[x]在调用之前如果不存在会创建mp[x]=0，对记忆化搜索的过程有影响，所以记忆化x是否保存结果的时候应该使用mp.count(x)

代码；

ABC300F

题面

#include 
using namespace std;

#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define PII pair
#define de(a) cout << #a << " = " << a << "\n";
#define deg(a) cout << #a << " = " << a << " ";
#define endl "\n"
#define int long long
#define LL long long
const int mod = 998244353;
const int N = 1e6 + 5;
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};

int POW(int a, int b)
{
	int res = 1;
	while (b)
	{
		if (b & 1)
			res *= a;
		a *= a;
		res %= mod;
		a %= mod;
		b >>= 1;
	}
	res %= mod;
	return res;
}
map mp;

int dp(int n, int inv)
{
	if (mp.count(n))
		return mp[n];

	int ans = 0;
	for (int i = 2; i <= 6; i++)
	{
		if (n % i == 0)
		{
			ans += dp(n / i, inv);
			ans % +mod;
		}
	}
	mp[n] = ans * inv % mod;
	return mp[n];
}

void solve()
{
	int inv = POW(5, mod - 2);
	int n;
	cin >> n;
	mp[1] = 1;
	cout << dp(n, inv);
}

signed main()
{
	FAST;
	int t = 1;
	// cin >> t;
	while (t--)
		solve();

	return 0;
}

思路

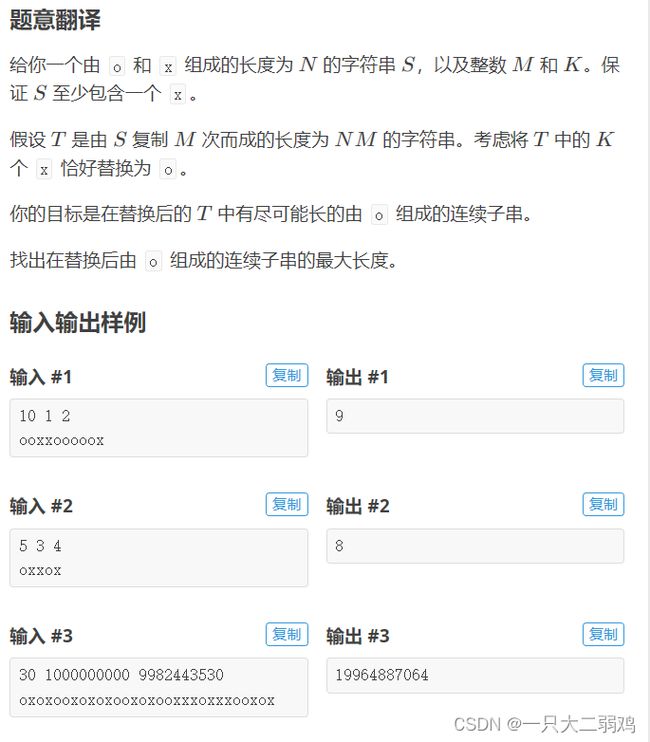
先抛出结论：起点一定在1-N某个点（假设字符串第一个字符的下标为1）

证明：首先T是由M个S串拼接而成，假设最优方案具有从第N+1或者更晚的某个字符开始的最长连续的o，然后对于第i个字符，我们决定使用第i-N个字符去替代它(他们是相同的，在不考虑修改的情况下，而且这种情况必定存在，因为i>=N+1)。

得到这个结论之后，就可以O(N)枚举起点，那怎么得到终点呢？

？？暴力枚举，从i（1<=i<=N）开始，枚举j(N<=j<=NM)直到i-j这个区间内的x的个数大于k停止，此时答案即为j-i+1 （i-j范围内的x最多出现k次）。思路没错，但是这样跑直接T飞。

写到这一步就可以二分了，sum[i]表示从1-i这个区间内x的个数是多少。只需要求出1-N的即可，因为后面的NM-N个字符，每N个都与前1-N个字符相同，那对于一个大于N的下标i可以这样得到1-i中的x的个数

int f(int x, int n, vector &rw) // 返回从1-x有多少个x
{//x为终点下表，n即为上文的N，也就是S串的长度，rw是前缀和数组，rw[i]代表1-i有多少个x
	int res = (x / n) * rw[n];
	int rem = x % n;
	res += rw[rem];
	return res;
}

总结：

枚举起点i（1<=i<=N），二分终点j（i<=j<=NM），[i,j]这个闭区间中x的个数<=k

代码：

#include 
using namespace std;

#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define PII pair
#define de(a) cout << #a << " = " << a << "\n";
#define deg(a) cout << #a << " = " << a << " ";
#define endl "\n"
#define int long long
#define LL long long
const int mod = 1e9 + 7;
const int N = 1e6 + 5;
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};

int f(int x, int n, vector &rw) // 返回从1-x有多少个x
{
	int res = (x / n) * rw[n];
	int rem = x % n;
	res += rw[rem];
	return res;
}

void solve()
{
	int n, m, k;
	cin >> n >> m >> k;
	string s;
	cin >> s;
	vector rw(n + 1, 0);
	for (int i = 0; i < n; i++)
	{
		rw[i + 1] = rw[i];
		if (s[i] == 'x')
			rw[i + 1]++;
	}

	int res = 0;
	for (int i = 1; i <= n; i++)
	{
		int fbeg = f(i - 1, n, rw); // 1-i-1位置有多少x
		int l = i, r = n * m;
		while (l <= r)
		{
			int mid = l + r >> 1;
			if (f(mid, n, rw) - fbeg <= k)
			{
				// f(mid, n, rw) - fbeg从i-mid有多少x
				l = mid + 1;
			}
			else
			{
				r = mid - 1;
			}
		}
		res = max(r - i + 1, res);
	}
	cout << res << endl;
}

signed main()
{
	FAST;
	int t = 1;
	// cin >> t;
	while (t--)
		solve();

	return 0;
}

ABC300G

参考：AtCoder Beginner Contest 300——A-G题讲解atcoder比赛阿史大杯茶的博客-CSDN博客

官方题解：Editorial - UNIQUE VISION Programming Contest 2023 Spring(AtCoder Beginner Contest 300)

#include 
using namespace std;

#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define PII pair
#define de(a) cout << #a << " = " << a << "\n";
#define deg(a) cout << #a << " = " << a << " ";
#define endl "\n"
#define int long long
#define LL long long
const int mod = 1e9 + 7;
const int N = 1e6 + 5;
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};

int n, p;

void push(vector &a, int num) // 将与num结合合法的数全部加进来
{
	int sz = a.size();
	for (int i = 0; i < sz; i++)
	{
		int t = a[i];
		while (1)
		{
			t *= num;
			if (t > n)
				break;
			a.push_back(t);
		}
	}
}

void solve()
{
	vector prime = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};

	cin >> n >> p;

	while (p < prime.back()) // 将大于p的质因数删去
		prime.pop_back();

	vector frt = {1}, bck = {1};
	for (auto &c : prime)
	{
		if (frt.size() < bck.size())
			push(frt, c); // 采用这种方式降低push函数里面的时间复杂度
		else
			push(bck, c);
	}

	sort(frt.begin(), frt.end());
	sort(bck.begin(), bck.end());
	int res = 0;
	for (int i = 0, j = bck.size() - 1; i < frt.size(); i++) // 双指针找合法数
	{
		int left = n / frt[i];
		while (j >= 0 && left < bck[j])
			j--;
		if (j < 0)
			break;
		res += j + 1;
	}
	cout << res << endl;
}

signed main()
{
	FAST;
	int t = 1;
	// cin >> t;
	while (t--)
		solve();

	return 0;
}