图像多目标跟踪

目标跟踪（Object Tracking）是自动驾驶中常见的任务，根据跟踪目标数量的不同，目标跟踪可分为：

• 单目标跟踪（Single Object Tracking，SOT）
• 多目标跟踪（Multi-Objects Tracking，MOT）

目标跟踪所要做的是根据传感器量测序列确定真实目标的数量以及每个目标的对应状态（位置、速度、航向等）

多目标跟踪常用的两个算法为：卡尔曼滤波和匈牙利匹配两个算法

        匈牙利匹配算法用于匹配前后帧目标，因为目标检测器的不稳定（垃圾）往往容易丢失目标或目标框的位置偏移，影像匈牙利匹配的结果。

        卡尔曼滤波可以基于t时刻的历史状态信息（目标框的位置x,y,w,h）预计t+1时刻的状态信息，出现丢失目标的时候，比匹配丢失前一帧目标位置，目标的运动轨迹要平滑的多，也不会存在匹配不到目标的情况。

        也可以根据观测量（例如：位置、检测目标给的信息）和在历史观测信息上基于状态转换矩阵（例：变化速度）估计出来的预测量。观测量和预测量都是服从正态分布，利用高斯计算公式将他们叠加起来，计算一个比较好的结果。

 

卡尔曼滤波算法

        在多目标跟踪中，使用的是最基础的 Kalman filter 算法，卡尔曼的过程如下所示，主要是预测和更新的过程：

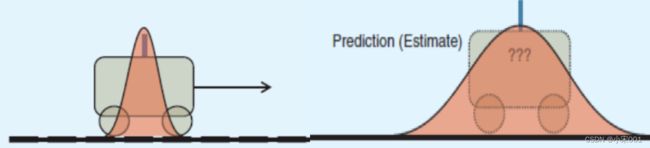
 预测过程方程：N（均值，方差）

        这个过程类似根据小车左侧位置，估计下一时刻的右侧的位置和方差，不过在目标跟踪中是预测的目标框的位置

 公式①预测t时刻的x，也就是高斯分布的均值变化

x:track在t−1时刻的均值（t时刻的目标检测框）, F:状态转移矩阵（线性变化）

在上图中

cx，cy: 边界框的中心点

w, h: 边界框的宽和高

vx, vy, vw, vh: 变化速度

dt：前后帧之间的差cx'=cx+dtvx

公式②预测t时刻的P，高斯分布的方差（误差）变化，

        我们获取的观测值（目标检测框）和预测值（通过状态转移矩阵推测出来的），都会存在一定的误差。

        P:track在t−1时刻的协方差,Q:系统噪声矩阵

         Q:初始值比较小 F:初始为对角线为1的矩阵

        这个方差P（随机举例如下图）就是我们在估计中的不确定矩阵，而这个矩阵需要我们自己进行微调，越大的值代表误差越大，这个方差在迭代更新过程中会逐渐减小。

 

 更新过程

        基于 t 时刻的检测结果（测量值）和根据跟踪轨迹预测目标在 t 时刻的状态（预测值），得到一个在 t 时刻更精确的结果（状态），通过高斯公式计算类似于下图中绿色的部分。

 在目标跟踪过程中就是将两个框叠加在一起！！！！

更新公式如下所示：

 

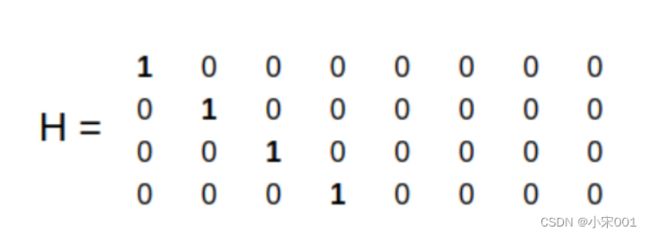
        公式③中 z 为 detection 的均值向量，不包含速度变化值，即 z=[x, y, a, h]，H 称为转移矩阵如下所示，它将 track 的均值向量 x’ 映射到检测空间，该公式计算 detection 和 track 的均值误差 y

        公式 ④中，R 为检测器的 噪声矩阵（随机举例如下图），它是一个 4x4 的对角矩阵，对角线上的值分别为中心点两个坐标以及宽高的噪声，以任意值初始化，一般设置宽高的噪声大于中心点的噪声。该公式先将协方差矩阵 P’ 映射到检测空间，然后再加上噪声矩阵 R。

         （上面的矩阵的值代表，对于cx和cy的误差没有那么大，而长和宽的预测的误差比较大）

        公式 ⑤中，计算 卡尔曼增益 K， 卡尔曼增益用于估计误差的重要程度；

        公式 ⑥ 和公式 ⑦中，计算更新后的均值向量 x 和协方差矩阵 P

 匈牙利匹配：

        在目标跟踪中，不同时刻的物体位置会发生变化，但我们需要让它保持同一个目标。

      建立一个二分图，有当前帧t=1 和前一帧t=0 的节点，通过计算优化两帧各个目标的互相的距，构建的混合线性整型，使用匈牙利或者求解器进行计算，得到两帧目标之间的匹配关系。

 

公式如下：

优化代价f可以是两个框体的欧式距离矩阵

 

          可以是两物体之间iou距离矩阵（在iou距离时，不是求最小而是求最大，可以使用1-iou转换为最最小值）

        也可以是两个框体中图像特征中的相似度距离矩阵

 有的算法中使用iou和特征相似度结合构建新的约束矩阵。

 

 这篇文章挺好可以看一下：

图说卡尔曼滤波，一份通俗易懂的教程 - 知乎 (zhihu.com)