hand crafted feature：histogram（直方图）

直方图是什么

约定

为了方便叙述，此处关于直方图概念的讨论做一些约束：

• 图像数据类型是uint8类型，可表达的数值范围是[0, 255]
• 以灰度图作为讨论的基础，此时的直方图可进一步称为灰度直方图

但是也应当悉知，当我们在上述约束下把直方图的概念讨论清楚后，相应的理论同样适用于其他数据类型，如float，也适用于彩色图像。

灰度级

我们可以把[0, 255]的范围划分为多个区间，每一个区间就称为一个灰度级。

特别的，当我们将[0, 255]平均划分为256个区间时，每一个数字就对应一个灰度级。

直方图的定义

直方图是图像每一个灰度级与该灰度级出现的概率的对应关系，由于灰度级是离散的，所以直方图是一个离散函数。假设一张图像的像素总数是$N$，属于某个灰度级$g$的像素总数是$N_g$，那么该灰度级出现的概率就是
$$P_g=N_g/N$$
此时，直方图的横坐标就是灰度级$g$，而纵坐标就是概率$P_g$。

也可以将直方图纵坐标定义为$N_g$，即灰度级中的像素总数，但是这种定义不利于进一步的理论理解，比如直方图均衡化相关理论。但是程序计算的结果通常以像素数目这种定义方式返回。

直方图计算方法

素材

素材使用美女lena，图片下载网址：https://www.ece.rice.edu/~wakin/images/lena512color.tiff

程序

直方图的计算方法很简单，核心思想就是计数。
将待统计的像素值区域划分成一个个的区间（在计算直方图时我们一般把这样的区间称为bin），区间划分方式一般是等分（当然同学你真的想不等分也不是不可以），然后统计图像落在各个区间中的像素的数量即可得到直方图。

下面的程序使用两种方式计算直方图，一种是自己写的函数compute_histogram，另一种是opencv的库函数cv2.calcHist，我们可以进行对比验证，看看自写函数与opencv的库函数计算的结果是否一致。我已经验证了是一致的。吐槽一下，opencv库函数的入参形态有点怪异。。。

请注意，彩色图像的直方图应当对每个通道分别计算，而不是对所有通道一起计算。
计算程序如下，文件名保存为histogram.py

# -*- coding: utf-8 -*-
import cv2
import numpy as np


def compute_histogram(image, channel, hist_size=256, ranges=None):
    """
    Description:
    ------------
    compute histogram of image

    Inputs:
    -------
    image: image data (ndarray)
    channel: channel of image to be computed
    hist_size: bins number of histogram
    ranges: data range to be counted

    Outputs:
    --------
    hist: histogram of image for a certain channel
    """
    # check arguments
    if ranges is None:
        ranges = [0, 256]
    assert hist_size > 1, 'hist_size must be greater than 1'
    assert image.ndim == 2 or image.ndim == 3, 'image dimension must be 2 or 3'
    if image.ndim == 3:
        assert channel < image.shape[2], \
            'channel must be less than image channels'
        image = image[:, :, channel]
    # compute histogram
    bin_width = (ranges[1] - ranges[0]) / hist_size
    hist = np.zeros([hist_size])
    for i in range(hist_size):
        bin_beg = ranges[0] + i * bin_width
        bin_end = ranges[0] + (i + 1) * bin_width
        hist[i] = np.sum((image >= bin_beg) & (image < bin_end))
    return hist


def normalize_histogram(hist):
    """
    Description:
    ------------
    normalize histogram by dividing sum of hist

    Inputs:
    -------
    hist: histogram

    Outputs:
    --------
    hist: normalized histogram
    """
    hist /= np.sum(hist)
    return hist


def plot(hist, color, image_height, ratio):
    """
    Description:
    ------------
    plot histogram by 2D image

    Inputs:
    -------
    hist: histogram
    color: color of histogram image
    image_height: height of histogram image
    ratio: max height of hist over image height

    Outputs:
    --------
    hist_image: histogram image
    """
    image_width = hist.shape[0]
    if isinstance(color, (int, float)):
        hist_image = np.zeros([image_height, image_width], dtype=np.uint8)
    else:
        assert len(color) == 3, 'length of color must be 3 if it is not scalar'
        hist_image = np.zeros([image_height, image_width, 3], dtype=np.uint8)

    hist /= np.max(hist)
    for x in range(image_width):
        pt1 = (x, image_height)
        pt2 = (x, int(image_height - np.round(hist[x] * image_height * ratio)))
        cv2.line(hist_image, pt1, pt2, color=color)
    return hist_image


def is_equal(hist_a, hist_b):
    """
    Description:
    ------------
    check whether two histograms are equal

    Inputs:
    -------
    hist_a and hist_b are two histograms

    Outputs:
    --------
    return True if two histograms are equal, and False if not
    """
    assert hist_a.ndim == hist_b.ndim == 1, 'hist must be rank-1 array'
    assert hist_a.shape[0] == hist_b.shape[0]
    return np.all(hist_a == hist_b)


if __name__ == '__main__':
    # parameters
    HIST_SIZE = 256
    RANGES = [0, 256]
    HIST_IMAGE_HEIGHT = 256
    RATIO = 0.9
    # read images
    color_image = cv2.imread('lena512color.tiff', cv2.IMREAD_UNCHANGED)
    gray_image = cv2.cvtColor(color_image, cv2.COLOR_BGR2GRAY)

    # gray image
    hist_gray = compute_histogram(gray_image, 0, HIST_SIZE, RANGES)
    hist_gray_cv2 = cv2.calcHist([gray_image], channels=[0], mask=None,
                                 histSize=[HIST_SIZE], ranges=RANGES)
    hist_gray_cv2 = np.squeeze(hist_gray_cv2)

    print(is_equal(hist_gray, hist_gray_cv2))
    hist_gray_image = plot(hist_gray, color=255,
                           image_height=HIST_IMAGE_HEIGHT, ratio=RATIO)

    # color image
    hist_blue = compute_histogram(color_image, 0, HIST_SIZE, RANGES)
    hist_green = compute_histogram(color_image, 1, HIST_SIZE, RANGES)
    hist_red = compute_histogram(color_image, 2, HIST_SIZE, RANGES)

    hist_blue_cv2 = cv2.calcHist([color_image], channels=[0], mask=None,
                                 histSize=[HIST_SIZE], ranges=RANGES)
    hist_green_cv2 = cv2.calcHist([color_image], channels=[1], mask=None,
                                  histSize=[HIST_SIZE], ranges=RANGES)
    hist_red_cv2 = cv2.calcHist([color_image], channels=[2], mask=None,
                                histSize=[HIST_SIZE], ranges=RANGES)
    hist_blue_cv2 = np.squeeze(hist_blue_cv2)
    hist_green_cv2 = np.squeeze(hist_green_cv2)
    hist_red_cv2 = np.squeeze(hist_red_cv2)

    print(is_equal(hist_blue, hist_blue_cv2),
          is_equal(hist_green, hist_green_cv2),
          is_equal(hist_red, hist_red_cv2))

    hist_blue_image = plot(hist_blue, color=(255, 0, 0),
                           image_height=HIST_IMAGE_HEIGHT, ratio=RATIO)
    hist_green_image = plot(hist_green, color=(0, 255, 0),
                            image_height=HIST_IMAGE_HEIGHT, ratio=RATIO)
    hist_red_image = plot(hist_red, color=(0, 0, 255),
                          image_height=HIST_IMAGE_HEIGHT, ratio=RATIO)

    cv2.imwrite('lena_gray.png', gray_image)
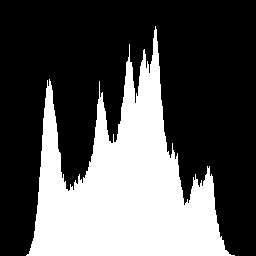
    cv2.imwrite('hist_gray.png', hist_gray_image)
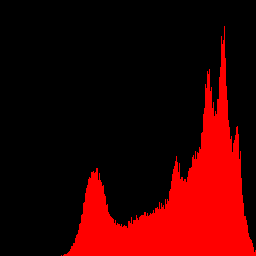
    cv2.imwrite('hist_blue.png', hist_blue_image)
    cv2.imwrite('hist_green.png', hist_green_image)
    cv2.imwrite('hist_red.png', hist_red_image)

上述程序将lena图转为灰度，然后计算了其直方图。而后又彩色的lena图分别计算了BGR三个通道的直方图。

计算结果

灰度图的直方图：

彩色图的直方图：

直方图的作用

作为图像特征

直方图可以用作图像特征，其特点如下：

• 是图像全局特征的表达
• 仅是图像色彩特征的表达
• 该特征的语义表达能力非常弱，或者换句直白点的话讲，这个特征比较挫

比如下面三张图，分别是ocean, sky1, sky2

ocean

sky1

sky2

我们分别计算这三张图的直方图特征，计算方法是对BGR三个通道分别计算直方图，而后将其串联起来作为特征。然后发现，因为ocean和sky1的色彩比较相近，所以两者相似度较高；而sky1和sky2尽管都是天空（即语义相近），但是因为色彩相差较大，所以相似度反而很低。

计算代码如下：

# -*- coding: utf-8 -*-
import cv2
import numpy as np
from histogram import compute_histogram

HIST_SIZE = 128


def cos_similarity(feature_a, feature_b):
    """
    Description:
    ------------
    compute cosine similarity of two features

    Inputs:
    -------
    feature_a and feature_b are ndarrays with same shape

    Outputs:
    --------
    cos_sim: cosine similarity
    """
    feature_a /= np.linalg.norm(feature_a)
    feature_b /= np.linalg.norm(feature_b)
    cos_sim = np.sum(feature_a * feature_b)
    return cos_sim


if __name__ == '__main__':
    image_sky1 = cv2.imread('sky1.png', cv2.IMREAD_UNCHANGED)
    image_sky2 = cv2.imread('sky2.png', cv2.IMREAD_UNCHANGED)
    image_ocean = cv2.imread('ocean.png', cv2.IMREAD_UNCHANGED)

    hist_sky1 = []
    hist_sky2 = []
    hist_ocean = []
    for ch in range(3):
        hist_sky1.append(compute_histogram(image_sky1, ch, HIST_SIZE))
        hist_sky2.append(compute_histogram(image_sky2, ch, HIST_SIZE))
        hist_ocean.append(compute_histogram(image_ocean, ch, HIST_SIZE))

    hist_sky1 = np.concatenate(hist_sky1)
    hist_sky2 = np.concatenate(hist_sky2)
    hist_ocean = np.concatenate(hist_ocean)

    sim_ocean_sky1 = cos_similarity(hist_sky1, hist_ocean)
    sim_sky1_sky2 = cos_similarity(hist_sky1, hist_sky2)

    print('cosine similarity of ocean vs sky: %0.4f' % sim_ocean_sky1)
    print('cosine similarity of sky1 vs sky2: %0.4f' % sim_sky1_sky2)

结果是：

cosine similarity of ocean vs sky: 0.7584
cosine similarity of sky1 vs sky2: 0.0907

调整图像色彩

我们可以对图像中的各个像素进行灰度变换从而调整图像色彩。比如在诸如Photoshop之类的图像编辑软件中，可以看到如下图所示的功能：

上图中横坐标是图像原始的灰度级，纵坐标是对图像进行一定的灰度变换后得到的灰度级，改变曲线就可以改变输入输出之间的灰度映射关系，如果对三个通道分别调整该曲线，就可以起到调整图像色彩的作用。需要注意的是，灰度变换本身并不需要计算直方图，而是只是需要对其进行观察。

此处不详细讨论，后面可以专门写一个灰度变换的主题。