数据结构笔记--链表经典高频题
目录
前言
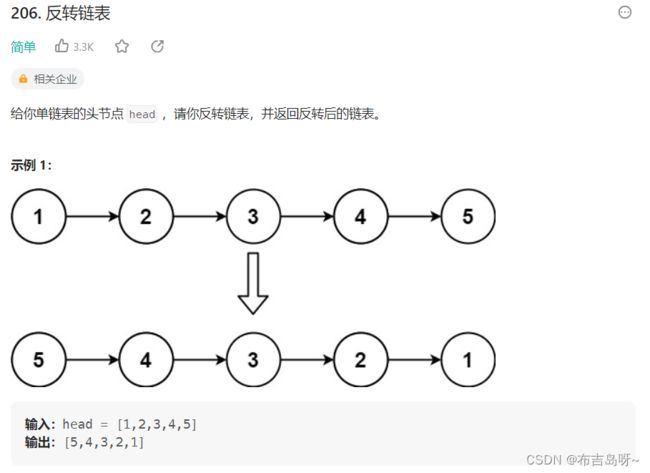
1--反转单向链表
2--反转单向链表-II
3--反转双向链表
4--打印两个有序链表的公共部分
5--回文链表
6--链表调整
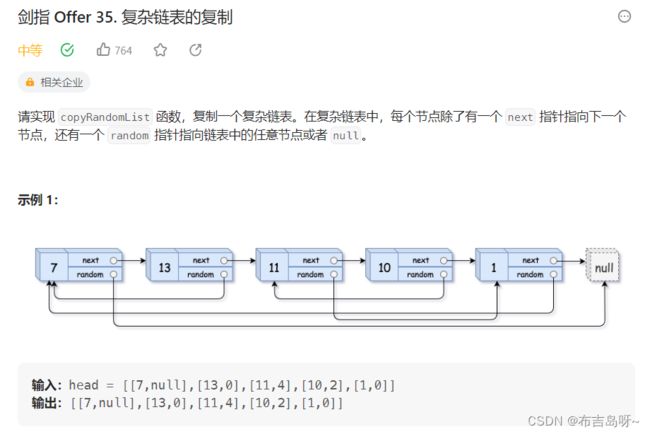
7--复制含有随机指针结点的链表
8--两个单链表相交问题
前言
面经:
针对链表的题目,对于笔试可以不太在乎空间复杂度,以时间复杂度为主(能过就行,对于任何题型都一样,笔试能过就行);对于面试,时间复杂度依然处在第一位,但要力求空间复杂度最低的算法(突出亮点);
链表题的重要技巧包括:使用额外的数据结构记录(例如哈希表等),使用快慢指针的思想;
1--反转单向链表
笔试解法:
借助栈先进后出,可以遍历把结点存到栈中,然后不断出栈,这样结点的顺序就反转了;
时间复杂度为O(n),空间复杂度为O(n);
#include
#include
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL) return head;
std::stack st;
while(head != NULL){
st.push(head);
head = head->next;
}
ListNode *new_head = new ListNode(0);
ListNode *tmp = new_head;
while(!st.empty()){
tmp->next = st.top();
st.pop();
tmp = tmp->next;
}
tmp->next = NULL;
return new_head->next;
}
};
int main(int argc, char *argv[]){
ListNode *Node1 = new ListNode(1);
ListNode *Node2 = new ListNode(2);
ListNode *Node3 = new ListNode(3);
ListNode *Node4 = new ListNode(4);
ListNode *Node5 = new ListNode(5);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Node4->next = Node5;
Solution S1;
ListNode *res = S1.reverseList(Node1);
while(res != NULL){
std::cout << res->val << " ";
res = res->next;
}
return 0;
} 面试解法:
不借助栈或递归,通过迭代将空间复杂度优化为O(1);
利用一个额外的前驱结点 pre 来存储当前结点 cur 的前一个结点,不断更新 pre 和 cur即可;
#include
#include
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL) return head;
ListNode *pre = NULL;
ListNode *cur = head;
while(cur != NULL){
ListNode* next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
};
int main(int argc, char *argv[]){
ListNode *Node1 = new ListNode(1);
ListNode *Node2 = new ListNode(2);
ListNode *Node3 = new ListNode(3);
ListNode *Node4 = new ListNode(4);
ListNode *Node5 = new ListNode(5);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Node4->next = Node5;
Solution S1;
ListNode *res = S1.reverseList(Node1);
while(res != NULL){
std::cout << res->val << " ";
res = res->next;
}
return 0;
} 2--反转单向链表-II
主要思路:
使用三个指针,指针 pre 指向反转区域外的第一个节点,即上图中的 1;指针 cur 指向当前指针,指针 next 指向 cur 的下一个指针;
遍历链表,每次将 next 指针头插,具体过程可以参考官方题解;
#include
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int left, int right) {
ListNode *dummyNode = new ListNode(-1);
dummyNode->next = head;
ListNode *pre = dummyNode;
ListNode *cur;
ListNode *next;
// 经过循环之后,pre指向反转区域前的第一个节点
for(int i = 0; i < left - 1; i++){
pre = pre->next;
}
cur = pre->next; // cur指向反转区域的第一个节点
for(int i = 0; i < right - left; i++){
next = cur->next;
cur->next = next->next; // cur指向next的下一个节点,因为next节点要头插到pre节点后面
next->next = pre->next; // next节点头插,指向原来的第一个节点
pre->next = next; // next节点头插到pre节点后面
}
return dummyNode->next;
}
};
int main(){
ListNode *Node1 = new ListNode(1);
ListNode *Node2 = new ListNode(2);
ListNode *Node3 = new ListNode(3);
ListNode *Node4 = new ListNode(4);
ListNode *Node5 = new ListNode(5);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Node4->next = Node5;
Solution S1;
int left = 2, right = 4;
ListNode *res = S1.reverseBetween(Node1, left, right);
while(res != NULL){
std::cout << res->val << " ";
res = res->next;
}
return 0;
} 3--反转双向链表
主要思路:
与反转单向链表类似,使用 pre,cur 和 next 指向前一个节点,当前节点和后一个节点,不断遍历更新三个指针所指向的节点即可,并修改对应的前驱指针和后驱指针;
#include
#include
struct ListNode {
int val;
ListNode *pre;
ListNode *next;
ListNode() : val(0), pre(nullptr), next(nullptr) {}
ListNode(int x) : val(x), pre(nullptr), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), pre(nullptr), next(next) {}
};
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL) return head;
ListNode *pre = NULL;
ListNode *cur = head;
while(cur != NULL){
ListNode* next = cur->next;
cur->next = pre;
cur->pre = next;
pre = cur;
cur = next;
}
return pre;
}
};
int main(int argc, char *argv[]){
ListNode *Node1 = new ListNode(1);
ListNode *Node2 = new ListNode(2);
ListNode *Node3 = new ListNode(3);
ListNode *Node4 = new ListNode(4);
ListNode *Node5 = new ListNode(5);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Node4->next = Node5;
Node2->pre = Node1;
Node3->pre = Node2;
Node4->pre = Node3;
Node5->pre = Node4;
Solution S1;
ListNode *res = S1.reverseList(Node1);
while(res != NULL){
std::cout << res->val << " ";
if(res->pre != NULL) std::cout << res->pre->val;
std::cout << std::endl;
res = res->next;
}
return 0;
} 4--打印两个有序链表的公共部分
给定两个有序链表的头指针 head1 和 head2,打印两个链表的公共部分;要求时间复杂度为O(n),额外空间复杂度要求为 O(1);
主要思路:
类似于归并排序,由于两个链表时有序的,因此可以使用两个指针 i 和 j 分别指向两个链表;
对于小的链表节点,指针后移;
当比较到两个指针相等时,打印节点的值,两个指针 i 和 j 同时后移;
#include
#include
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
std::vector printlist(ListNode* head1, ListNode* head2) {
std::vector res;
if(head1 == NULL || head2 == NULL) return res;
ListNode *i = head1;
ListNode *j = head2;
while(i != NULL && j != NULL){
// 小的后移
if(i->val < j->val) i = i->next;
else if(i->val > j->val) j = j->next;
else{ // 相等同时后移
res.push_back(i);
i = i->next;
j = j->next;
}
}
return res;
}
};
int main(int argc, char *argv[]){
ListNode *Node1 = new ListNode(1);
ListNode *Node2 = new ListNode(2);
ListNode *Node3 = new ListNode(5);
ListNode *Node4 = new ListNode(0);
ListNode *Node5 = new ListNode(2);
ListNode *Node6 = new ListNode(3);
ListNode *Node7 = new ListNode(5);
Node1->next = Node2;
Node2->next = Node3;
Node4->next = Node5;
Node5->next = Node6;
Node6->next = Node7;
Solution S1;
std::vector res = S1.printlist(Node1, Node4);
for(ListNode * node : res) std::cout << node->val << " ";
return 0;
} 5--回文链表
主要思路:
面试做法可以参考反转单向链表,将链表反转,与原链表的结点进行比较即可,当反转链表与原链表的结点不相等,表明不是回文链表;
空间复杂度 O(n),时间复杂度 O(n);
#include
#include
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
bool isPalindrome(ListNode* head) {
if(head == NULL) return true;
std::stack st;
ListNode *tmp = head;
while(tmp != NULL){
st.push(tmp);
tmp = tmp->next;
}
while(!st.empty()){
if(head->val != st.top()->val) return false;
head = head->next;
st.pop();
}
return true;
}
};
int main(int argc, char *argv[]){
ListNode *Node1 = new ListNode(1);
ListNode *Node2 = new ListNode(2);
ListNode *Node3 = new ListNode(2);
ListNode *Node4 = new ListNode(1);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Solution S1;
bool res = S1.isPalindrome(Node1);
if(res) std::cout << "true" << std::endl;
else std::cout << "false" << std::endl;
return 0;
} 主要思路:
笔试解法:上述解法的空间复杂度是 O(n),使用快慢指针将空间复杂度优化为 O(1);
主要原理是将链表由 1→2→1→2→1 构建为 1→2→1←2←1 的形式,从两端遍历进行比较;
#include
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
bool isPalindrome(ListNode* head) {
if(head == NULL) return true;
ListNode *i = head;
ListNode *j = head;
while(j->next != NULL && j->next->next != NULL){
i = i -> next;
j = j -> next -> next;
}
j = i->next; // right part first node
i->next = NULL;
ListNode *tmp = NULL;
while(j != NULL){
tmp = j->next;
j->next = i;
i = j;
j = tmp;
}
j = i; // 最后一个结点
i = head;
while(i != NULL && j != NULL){
if(i->val != j ->val) return false;
i = i->next;
j = j->next;
}
return true;
}
};
int main(int argc, char *argv[]){
ListNode *Node1 = new ListNode(1);
ListNode *Node2 = new ListNode(2);
ListNode *Node3 = new ListNode(2);
ListNode *Node4 = new ListNode(1);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Solution S1;
bool res = S1.isPalindrome(Node1);
if(res) std::cout << "true" << std::endl;
else std::cout << "false" << std::endl;
return 0;
} 6--链表调整
将单向链表按某值划分成左边小、中间相等、右边大的形式;
题目:给定一个单链表的头结点head,结点的值类型是整型,再给定一个整数pivot,实现一个调整链表的的函数,将链表调整为左部分都是值小于pivot的结点,中间部分都是值等于pivot的结点,右部分都是值大于pivot的结点;
要求:调整后所有小于、等于或大于pivot的结点之间的相对顺序和调整前一样,时间复杂度为O(n),空间复杂度为O(1);
#include
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* change(ListNode* head, int pivot) {
if(head == NULL) return head;
ListNode* SH = NULL; // small head
ListNode* ST = NULL; // small tail
ListNode* EH = NULL; // equal head
ListNode* ET = NULL; // equal tail
ListNode* LH = NULL; // large head
ListNode* LT = NULL; // large tail
ListNode* tmp;
while(head != NULL){
tmp = head->next; // 下一个结点
head->next = NULL;
// 抽每一个结点出来进行比较
if(head->val < pivot){
if(SH == NULL && ST == NULL){
SH = head;
ST = head;
}
else{
ST->next = head;
ST = ST->next;
}
}
else if(head->val == pivot){
if(EH == NULL && ET == NULL){
EH = head;
ET = head;
}
else{
ET->next = head;
ET = ET->next;
}
}
else{
if(LH == NULL && LT == NULL){
LH = head;
LT = head;
}
else{
LT->next = head;
LT = LT->next;
}
}
head = tmp; // 比较下一个结点
}
// 首尾相连
if(ST != NULL){// 有小于区域
ST->next = EH;
ET = ET == NULL ? ST : ET; // 没有等于区域,ET变成ST
}
if(ET != NULL) ET->next = LH;
return SH != NULL ? SH : (EH != NULL ? EH : LH);
}
};
int main(int argc, char *argv[]){
ListNode *Node1 = new ListNode(4);
ListNode *Node2 = new ListNode(6);
ListNode *Node3 = new ListNode(3);
ListNode *Node4 = new ListNode(5);
ListNode *Node5 = new ListNode(8);
ListNode *Node6 = new ListNode(5);
ListNode *Node7 = new ListNode(2);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Node4->next = Node5;
Node5->next = Node6;
Node6->next = Node7;
Solution S1;
int pivot = 5;
ListNode* res = S1.change(Node1, pivot);
while(res != NULL){
std::cout << res->val << " ";
res = res->next;
}
return 0;
} 7--复制含有随机指针结点的链表
主要思路:
笔试解法,利用哈希表存储结点,即 key 表示原来的结点,value 表示复制的结点;
存储完毕后,遍历结点设置复制结点的 next 指针和 value 指针即可;
#include
#include
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
class Solution {
public:
Node* copyRandomList(Node* head) {
std::unordered_map hash;
Node *tmp = head;
while(tmp != NULL){
hash[tmp] = new Node(tmp->val);
tmp = tmp->next;
}
tmp = head;
while(tmp != NULL){
hash[tmp]->next = hash[tmp->next];
hash[tmp]->random = hash[tmp->random];
tmp = tmp->next;
}
return hash[head];
}
};
int main(int argc, char *argv[]){
Node* Node1 = new Node(7);
Node* Node2 = new Node(13);
Node* Node3 = new Node(11);
Node* Node4 = new Node(10);
Node* Node5 = new Node(1);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Node4->next = Node5;
Node1->random = NULL;
Node2->random = Node1;
Node3->random = Node5;
Node4->random = Node3;
Node4->random = Node1;
Solution S1;
Node* res = S1.copyRandomList(Node1);
while(res != NULL){
std::cout << res->val << " ";
res = res->next;
}
return 0;
} 主要思路:
面试解法,将空间复杂度优化为 O(1);
将原链表Ori_Node1 → Ori_Node2 → Ori_Node3 构造成 Ori_Node1 → New_Node1 → Ori_Node2 → New_Node2 → Ori_Node3 → New_Node3;
接着一对一对地去遍历链表,构建 random 指针;
最后将新旧链表分离,构建 next 指针即可;
#include
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
class Solution {
public:
Node* copyRandomList(Node* head) {
if (head == NULL) return NULL;
Node* tmp = head;
Node* next = NULL;
while(tmp != NULL){
next = tmp->next; // 原链表下一个结点
tmp->next = new Node(tmp->val); // 创建新结点
tmp->next->next = next; // 新结点指向原链表地下一个结点
tmp = next; // 更新tmp
}
tmp = head; // 遍历构建random指针
while(tmp != NULL){
next= tmp->next->next; // 一对一对遍历
tmp->next->random = tmp->random != NULL ? tmp->random->next : NULL;
tmp = next;
}
// 分离链表并构建next指针
tmp = head;
Node *res = head->next;
Node *copy;
while(tmp != NULL){
copy = tmp->next;
next = tmp->next->next; // 一对一对分离
tmp->next= next;
copy->next = next != NULL ? next->next : NULL;
tmp = next;
}
return res;
}
};
int main(int argc, char *argv[]){
Node* Node1 = new Node(7);
Node* Node2 = new Node(13);
Node* Node3 = new Node(11);
Node* Node4 = new Node(10);
Node* Node5 = new Node(1);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Node4->next = Node5;
Node1->random = NULL;
Node2->random = Node1;
Node3->random = Node5;
Node4->random = Node3;
Node4->random = Node1;
Solution S1;
Node* res = S1.copyRandomList(Node1);
while(res != NULL){
std::cout << res->val << " ";
res = res->next;
}
return 0;
}