机器学习之New Optimizers for Deep Learning 2（没听懂的读书笔记）

• Graph Neural Networks

Graph Neural Networks

  Graph是什么样？

  Graph有结点和边。

GNN用途
  （1）Classification
  假设现在有一大堆不同的分子，训练出一个Classifier可以判断分子会不会突变，dataset就是很多label好的data然后输入一个分类器没有看过的分子，让它判断这个分子会不会导致突变：

  （2）Generation

  （3）通过GNN推理剧中凶手
  现有一部剧，如果只通过人物特性推定每个人物是不是凶手，忽略了一个重要的东西–角色之间的关系，考虑所有人物的关系必须用到GNN。
  

  问题：如何利用卷积将节点嵌入特征空间?
  方法1：将卷积（相关）的概念推广到图–>Spatial-based convolution（基于空间的卷积）（空域或顶点域上直接对邻点操作）；
  方法2：回到卷积在信号处理中的定义–>Spectral-based convolution（基于谱的卷积）（在频率域上操作）；
  
  GNN路线图：

（一）Spatial-based GNN
  通过CNN的方法算出下一层layer的feature map：$h_3^0$代表第0层layer的第3个结点，现在要让$h_3^0$update成$h_3^1$，$h_3^0$的相邻结点有$h_0^0$、$h_2^0$、$h_4^0$，通过这几个结点来update下一层的hidden state，这件事情叫做Aggregate（合计）；把所有结点的feature集合起来代表整个graph叫做Readout（读出）。

一些模型：
  （1）NN4G（Neural Networks for Graph）

  其中，$h_3^0$=$x_3\cdot \overline{w_0}$，其它的结点同理可得，由此得到Hidden layer 0，$h_3^0$相邻结点为$h_0^0$、$h_2^0$、$h_4^0$，把这几个点Aggregate到Hidden layer 1的$h_3^1$，方法为把这三个结点相加后再经过一个transform之后，得到的结果再加上原本的input feature：
  $h_3^1=\widehat{w_{1,0}}(h_0^0+h_2^0+h_4^0)+\overline{w_1}\cdot x_3$
  
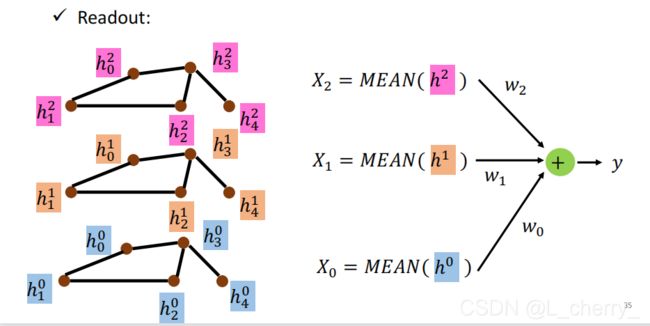
  Readout：叠了很多层之后，把每一层的node feature全部加起来后，各自经过一个transform再加起来得到一个feature，代表整个graph的一个feature：

  （2）DCNN（Diffusion-Convolution Neural Network）（扩散卷积神经网络）
  把input layer中跟$v_3$这个结点距离为1的结点加起来，取平均值，再乘于一个权值得到$h_3^0$：
  $h_3^0=w_3^{0}MEAN(d(3,\cdot )=1)$
  在Hidden layer 1时，仍旧使用input layer的feature去update，方式是把input layer中跟$v_3$这个结点距离为2的结点加起来（这里它距离自己本身也是2），取平均值，再乘于一个权值得到$h_3^1$：
  $h_3^1=w_3^{1}MEAN(d(3,\cdot )=2)$
  做完以上这些后，把每一层排成一个矩阵，然后叠起来：

  把以上叠起来的东西经过一个transform之后得到graph feature：

  （3）DGC（Diffusion Graph Convolution）（扩散图卷积）
  和DCNN的区别就是在最后得到graph feature之前，DCNN是把每一层叠在一起，而DGC是把每一层加起来：

  （4）MoNET（Mixture Model Networks）（混合模型网络）
  定义节点距离的度量值：例如$h_3^0$和$h_0^0$的距离为$u_{3,0}$，公式为：
      $u(x,y)=(\frac{1}{\sqrt{deg(x)}},\frac{1}{\sqrt{deg(y)}}{)}^T$
  其中deg(x)为x结点的度，例如$h_3^0$的度为3，那么deg($h_3^0$) = 3，$u_{3,0}=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{3}}{)}^T$；
  那么下一层的结点$h_3^1=w(\widehat{u_{3,0}})\times h_0^0+w(\widehat{u_{3,2}})\times h_2^0+w(\widehat{u_{3,4}})\times h_4^0$，其中$w(\cdot )$ is a NN，$\hat{u}$ is a transform from $u$。
  
  （5）GraphSAGE
  aggregation : mean,max-pooling,or LSTM

  （6）GAT(Graph Attention Networks)（图形注意网络）
  对邻居做attention：不同邻居的weight通过计算energy得到，如$h_3^0$和$h_0^0$之间的energy为$e_{3,0}$：

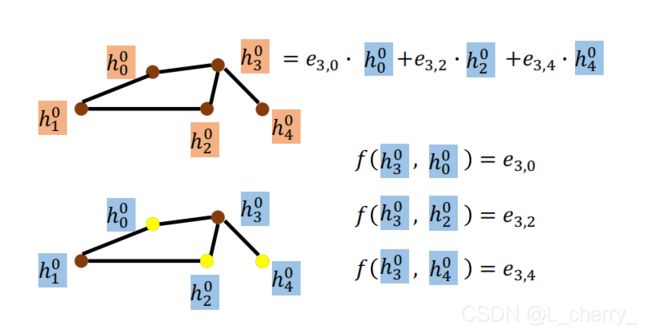
  通过weighted sum得到下一层的hidden layer的结点feature。
  
  （7）GIN(Graph Isomorphism Network)（图同构网络）
  结论：我们在做update最好用这样的方式：对于某一个结点$v$它在第k层，它的update方式是把它所有的相邻结点加起来，再加上某一个常数乘于它的上一层；
  注意：这里要使用sum（而不是mean或max）；MLP–Multi-layer Perceptron（多层感知机）;

（二）Spectral-based GNN
  Sprctral Graph Theory：
  Graph: G =(V,E),N = |V| （N为结点数量）；
  A$\in {\mathbb{R}}^{N\times N}$，adjacency matrix（邻接矩阵）（weight matrix）.如果$A_{i,j}$ = 0，说明两个结点并没有连在一起，如果两个结点连在一起，那么$A_{i,j}=w(i,j)$；
  现在只考虑无向图；
  D$\in {\mathbb{R}}^{N\times N}$，degree matrix；
$D_{i,j}=\{\begin{array}{cc}d(i)& ifi=j(SumofrowiinA)\\ 0& ifi\ne j\end{array}$
  $f$：V-> $\in {\mathbb{R}}^N$，signal on graph(vertices).$f(i)$ denotes the signal on vertex（顶点） $i$；
  假设有如图的一个graph，这个graph的顶点上有一些信号，$f(1)$等等，这个信号可以代表某种东西，比如气温：

  Graph Laplacian（拉普拉斯图）L = D - A , $L⩾0$（Positive semidefinite）（半正定）；
  L 是对称的；
  L = $U\Lambda U^T$ （spectral decomposition）（谱分解）；
  假设L是一个4x4的矩阵，那么可以分解为：
  $\Lambda =diag({\lambda }_0,...,{\lambda }_{N-1})\in {\mathbb{R}}^{N\times N}$；
  $U=[u_0,...,u_{N-1}]\in {\mathbb{R}}^{N\times N}$，orthonormal（正交的）；
  ${\lambda }_l$ is the frequency,$u_l$ is the basis corresponding（基对应） to $\lambda$；

  举例：现有一个graph，顶点上有一些信号$f(i)$：

  可以写出它的adjacent matrix：
$A=\left[\begin{array}{cccc}0& 1& 1& 0\\ 1& 0& 1& 1\\ 1& 1& 0& 0\\ 0& 1& 0& 0\end{array}\right]$
  可以写出它的degree matrix：
$D=\left[\begin{array}{cccc}2& 0& 0& 0\\ 0& 3& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 1\end{array}\right]$
  通过 D - A可以得到Laplacian：
$L=\left[\begin{array}{cccc}2& -1& -1& 0\\ -1& 3& -1& -1\\ -1& -1& 2& 0\\ 0& -1& 0& 1\end{array}\right]$
  通过分解得到：
$\Lambda =\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 3& 0\\ 0& 0& 0& 4\end{array}\right]$
$U=\left[\begin{array}{cccc}0.5& -0.41& 0.71& -0.29\\ 0.5& 0& 0& 0.87\\ 0.5& -0.41& -0.71& -0.29\\ 0.5& 0.82& 0& -0.29\end{array}\right]$
  得到信号graph如图：

频率越大，相邻两点之间的信号变化量就越大。
  
  解释什么是vertex frequency（顶点频率）：
  假设L是graph上的operator，$f$为图上的信号，让这个Laplacian乘于这个信号$Lf$，即$Lf=(D-A)f=Df-Af$；拿以上的那个例子来看，此时的$Lf$为一个四行一列的矩阵：

  其中，$Lf$中的a的计算过程为：

  式中的2x4，2为结点$v_0$的度，4为结点$v_0$上的信号，-2-4，减掉的是结点$v_0$两个邻居上的信号大小，整理一下就可以总结为a为结点$v_0$分别与两个邻居的差的和；
  如果要看能量就得计算$f^{T}Lf$（代表某一个结点i和某一个结点v之间信号能量差，即代表这个graph signal有多smooth）：

  回到刚才的信号graph图：

根据以上可以认为$\lambda$为vertex frequency。
  
  如何在graph上，把它的信号通过 Fourier transform转化到它的frequency domain？

  假设现有一个信号$x$，让它乘于一个U transform，得到这个信号在spectral domain上的信号：

  可以分析出每个信号在每一个不同频率成分上的大小：

  如何把spectral domain转换回vertex domain：

  以上的知识是为了找出在graph上做filter的方式，也就是要找出可以在graph上做Fourier transform和inverse Fourier transform的方式，将信号transform到spectral domain上直接相乘，即filter，做完之后，再inverse Fourier transform回到vertex domain；
  一个信号经过transform得到$\hat{x}$，把它乘于某一个filter 的frequency response，最后得到$\hat{y}$：

  得到的$\hat{y}$作为spectral domain的信号必须把它还原成vertex domain，要进行inverse Fourier transform，就是在$\hat{y}$前面在乘于一个U，得到最后要的信号y：

  现在想要train出一个model，给一个input x，希望可以学到一个filter，在$g_0(\Lambda )$经过这个filter之后可以得到一个y：

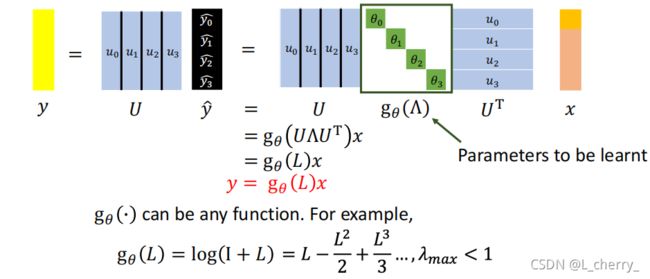
图中绿色框起来的参数是需要被学习的，它可以是任何function。
  但是这样做会有几个问题：(1)Learning complexity is O(N)!(2)选择$g_0(L)$时，会让这个model学到不需要它学的东西,不是一个localized filter。
  
以下是Spectral-based GNN的一些model：

  （1）ChebNet
  优点：速度快，并且可以局部化；
  $g_0(L)$得是一个多项式函数：
  $g_0(L)={\sum }_0^K{\theta }_k{L}^k$，现在就是K-localized，式中的${\theta }_k$是需要被学习的参数；
  现在要用它对x做filter：

其中的$g_0(\Lambda )$等价于$g_0(L)$：

  但是这里会出现time complexity为O($N^2$)的问题，解决方式：使用可以从L递归计算的多项式函数，Chebyshev polynomial（切比雪夫多项式）：

把$T_0(x)$转换成$T_0(\tilde{\Lambda })$：

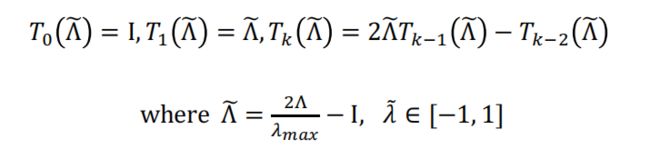
我们把之前filter的式子改变一下让它更好计算：

扩展计算：

  （2）GCN
  在刚才ChebNet式子的基础上，令K = 1：

  GNN上会用到的tasks、dataset、benchmark：

• Benchmark tasks(衡量model的方式)：
    - Semi-supervised node classification
    - Regression
    - Graph classification
    - Graph representation learning
    - Link prediction
• Common dataset
    - CORA:citation network. 2.7k nodes and 5.4k links
    - TU-MUTAG:188 molecules with 18 nodes on average
    
    （1）Graph classification
    对一整张图做Graph classification，SuperPixel MNIST ，CIFAR10
  

  （2）Regression
  很多不同的graph，大部分都是真实世界的分子，预测分子的溶解度：

  （3）Node classification
  利用Stochastic生成很多不同的图，辨认graph里的pattern，辨认不同的node属于那个cluster：

  （4）Edge classification
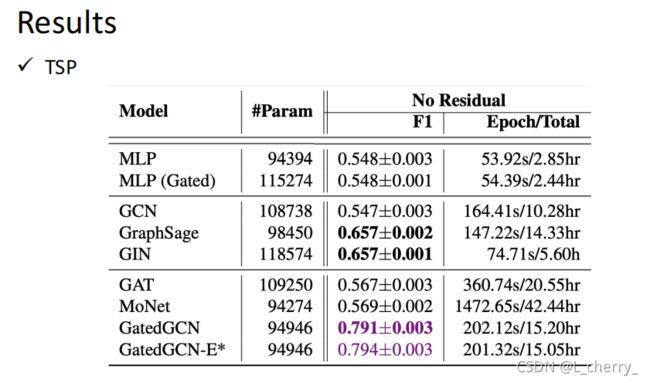
  路径不重复的情况下，从起点开始运行还能回到起点：

  结果：

  图片生成：

---

本文是对blibli上李宏毅机器学习2020的总结，如有侵权会立马删除。