simulink学习笔记：基于模型的控制和pid整定
在学习的时候发现了一个很好的学习simulink的网站，打算来练练手：Introduction: Simulink Control，过程中会涉及到搭建动力学模型和设计pid控制器（整定pid参数）。该模型描述的是火车的两节车厢，对前一节车厢施力，控制其速度按照跟随指定的方波。我在我的资源里也把我建好的所有模型放上去，大家可以直接下载。链接是
simulink基于模型的控制和pid整定配套模型文件
1. 搭建动力学模型
根据牛顿第二定律，我们画出受力图：
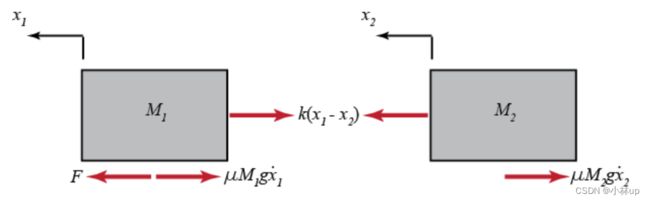
列出动力学方程：
Σ F 1 = F − k ( x 1 − x 2 ) − μ M 1 g x ˙ 1 = M 1 x ¨ 1 Σ F 2 = k ( x 1 − x 2 ) − μ M 2 g x ˙ 2 = M 2 x ¨ 2 \begin{aligned} \Sigma F_{1}&=F-k\left(x_{1}-x_{2}\right)-\mu M_{1} g \dot{x}_{1}=M_{1} \ddot{x}_{1} \\ \Sigma F_{2}&=k\left(x_{1}-x_{2}\right)-\mu M_{2} g \dot{x}_{2}=M_{2} \ddot{x}_{2} \end{aligned} ΣF1ΣF2=F−k(x1−x2)−μM1gx˙1=M1x¨1=k(x1−x2)−μM2gx˙2=M2x¨2
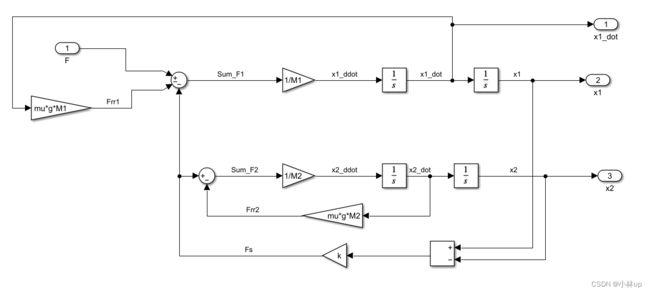
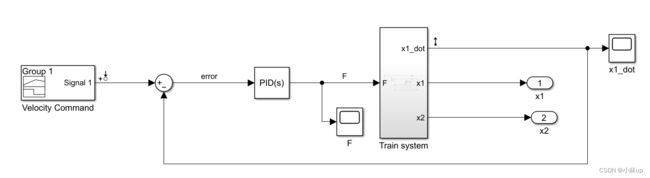
于是我们可以搭建如下图所示的模型，简单说一下搭建的思路，从动力学入手我们可以从加速度入手，将加速度单独拿到一边，另一边是合力除上质量，通过积分器可以把加速度依次变成速度和位移，而合力又昆虫用上位移和速度，这样就写成了一个闭环（使用积分器比微分器好，微分器容易出现不连续）。使用到的模块：Sum、Add、Gain、Integrator、Scope、Signal Gernerator。
链接给出了具体的搭建步骤，如果感兴趣可以去看一下：Introduction: Simulink Modeling。
关于参数的设置要先在工作区设置好。新建一个parameter.m文件和simulink文件在一起，写入参数：
parameter.m
clc
clear
M1 = 1;
M2 = 0.5;
k = 1;
F = 1;
mu = 0.02;
g = 9.8;
运行后加载后工作区，上面的模型才能运行！因为在诸如Gain的模块里写的是1/M1，M1是个变量，从工作区里得到。
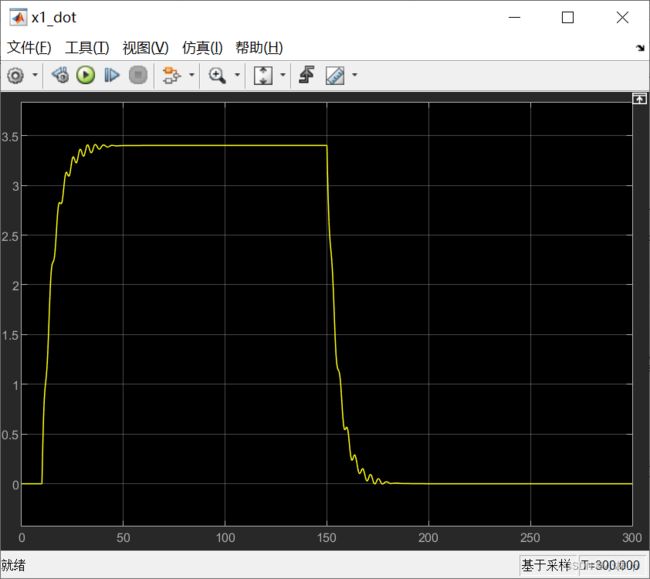
设置仿真的时间为1000，运行我们看到速度的幅度现在基本是±3.5，类似一个方波。
但是我们现在不能让其是我们想要的速度，于是我们接下来就就加入pid控制实现按我们规定的速度运行。
2. PID控制器的实现
2.1 开环效果
这一部分可以接上一步的train_model.slx操作，我写好的模型在train_model_pid1.slx中。
我们然后使用Out1和一个In1模块替换所有的Scope，如下图所示。我们还要给三个Out1分别命名为x1_dot、x1和x2，以及In1命名为F。
然后我们右键生成子系统
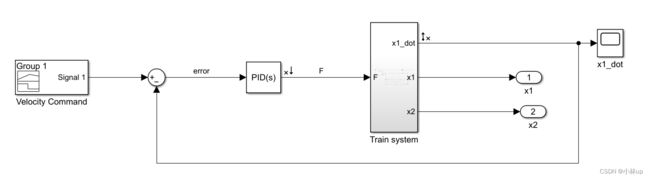
如图我们添加pid控制器，并且加入波形发生器signal builder。
对于pid我们的初始的设置为：kp=1，ki=0，kd=0。
我们设置波形为如图所示，时间长度为300s,在10秒从0阶跃到1，在150秒从1阶跃回0.
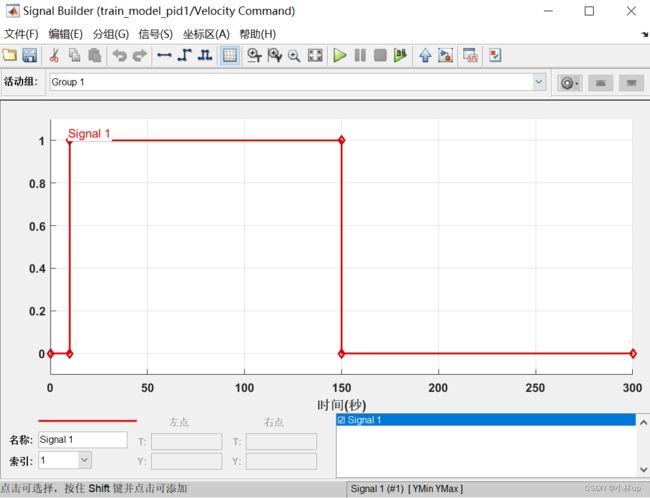
这里我们设置的仿真时间和信号发生器的时间是一样的，也是300s（后面的闭环效果也是一样的）。我们可以运行一下上面的模型看一下效果，和前面的动力学模型的效果是一样的。因为现在还没有加反馈。
2.1.1 提取开环模型
要注意的是，上面我们的模型框图并没有添加闭环的反馈。我们在PID控制器后面的信号线右键选择Linear Analysis Points，接着选择Open loop Input，然后会显示一个向下的箭头，
同样的我们可以在子模块的x1_dot输出信号线右键选择Linear Analysis Points，接着选择Open loop Output，然后会显示一个向上的箭头。
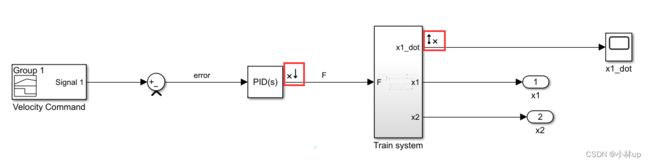
我们用模型线性化器提取模型。
点击Step我们可以看到输入阶跃信号的输出。这个输出和我们在simulink的输出是一样的。
我们可以调整一下图的坐标（后面的图都可以同样的操作），右键选择Properties。
改这两个参数我们可以看到
我们可以看到生成了线性化的模型linsys1，在Linear Analysis Workspace里面，
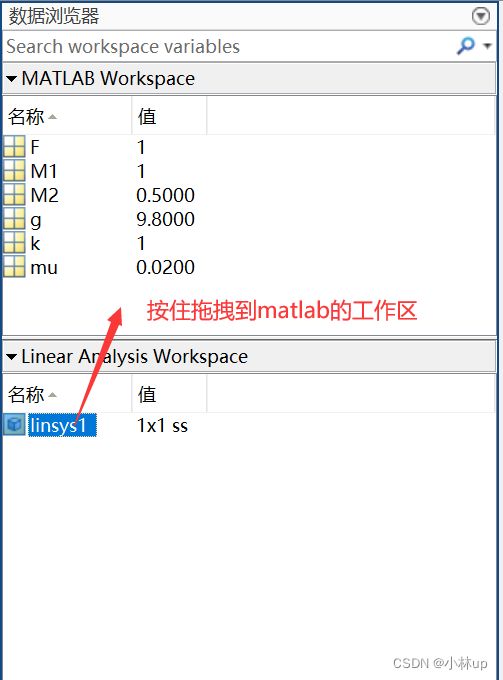
根据生成的模型我们可以计算反馈系统下的零极点。在命令行窗口输入：
sys_cl = feedback(linsys1,1);
p = pole(sys_cl)
z = zero(sys_cl)
这等价于下面的模型框图：
对上述情况的检查表明，原点存在零极点取消。此外，其余极点具有负数 实部和两个“最慢”的极点很复杂。这表明当前形式的闭环系统是稳定的 并且占主导地位的极点阻尼不足。我们接下来根据上面的分析运行看一下闭环的情况。
2.2 闭环效果
我们运行上面的模型，现在我们取消之前添加的Open loop Input和Open loop Output，还是右键再点一下Linear Analysis Points中的Open loop Input和Open loop Output就可以取消了。
我们还是运行一下闭环添加了反馈的效果。
2.2.1 闭环pid参数整定
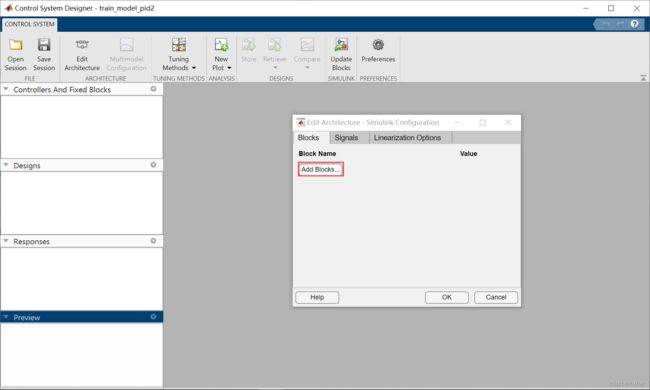
选择控制系统设计器。
点击Add Blocks。
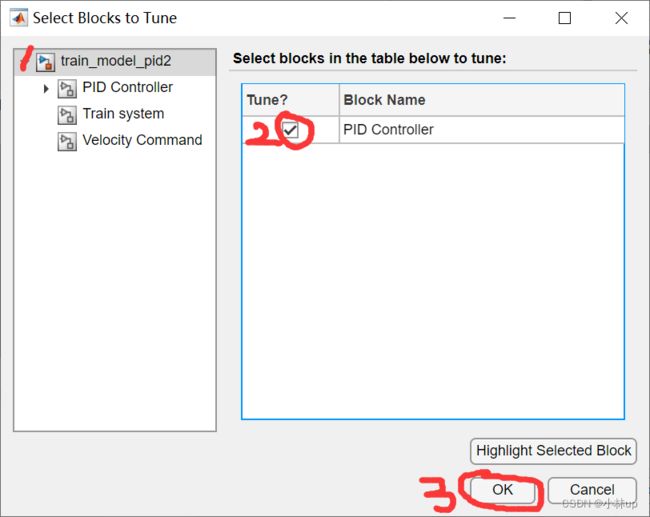
然后不要直接在Edit Architecture界面按OK，要回到模型，我们设置一下输入和输出（我的理解是一个参考输入和一个实际输出），我们在信号发生器后面的信号线右键选择Linear Analysis Points，接着选择Input Perturbation，然后会显示一个向下的加号箭头。
同样的我们可以在子模块的x1_dot输出信号线右键选择Linear Analysis Points，接着选择Output Measurement，然后会显示一个向上的箭头。
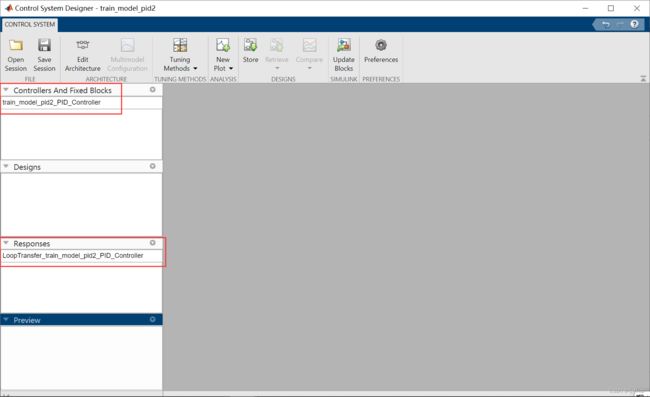
然后返回前面的Edit Architecture界面按OK，这步和前面的顺序不能反了，否则不能出现下面的Controllers And Fixed Blocks以及Responses。（可能只出现一个，我之前就是搞错了顺序只出现了Controllers And Fixed Blocks）
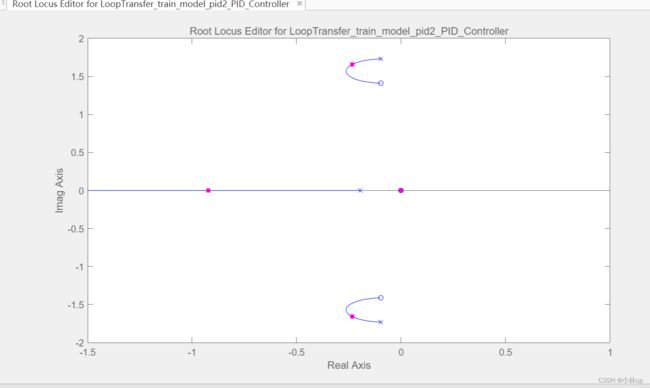
好了我们现在可以看一下根轨迹。如图选择Turning Method，选择Root Locus Editor。
点击plot
我们就出现了根轨迹。我们可以用鼠标“拖拽”标记闭环极点的粉红色框以图形方式完成 位置并将它们拖向开环极位置（用 x 标记）【这个就很神奇，动态调节】，可以自己尝试一下哈。
然后我们根据现在的这个系统绘制一下输出的响应，点击New Plot，然后点击New Step。
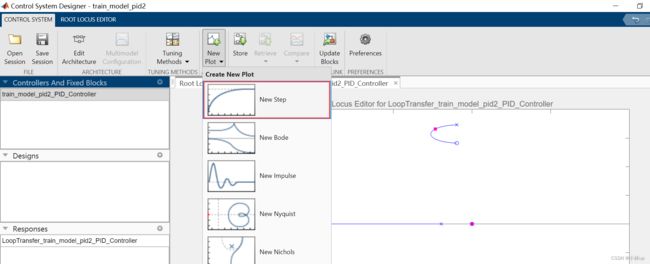
选择New input-output transfer response
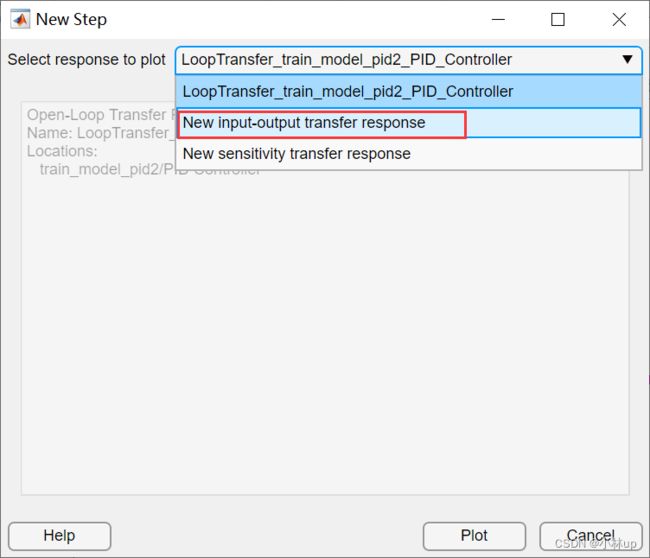
我们定义输入信号，在Specify input signal下点击Add signal to list
然后选择Select signal from model
点击回到模型点击信号发生器后面的那根信号线。
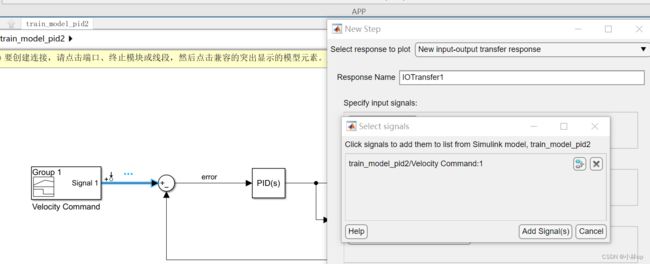
信号就出现了Select signals对话框里，再点击Add signal
我们定义输出信号
然后选择Select signal from model
点击回到模型点击子系统后面的那根x1_dot的信号线。
信号就出现了Select signals对话框里，再点击Add signal
点击Plot，我们绘制响应曲线。
结果如图所示：
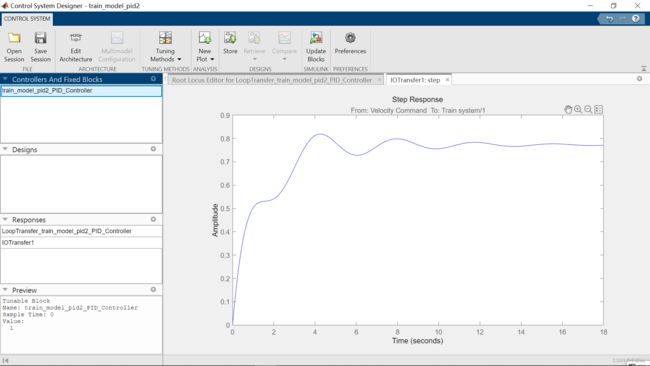
我们还是改变一下图的Properties，在图像上右键选Properties，改一下图的坐标轴的范围。
这和我们在simulink里仿真的模型的结果是一样的，我们看到存在稳态误差，积分器可以很好地减少稳态误差。
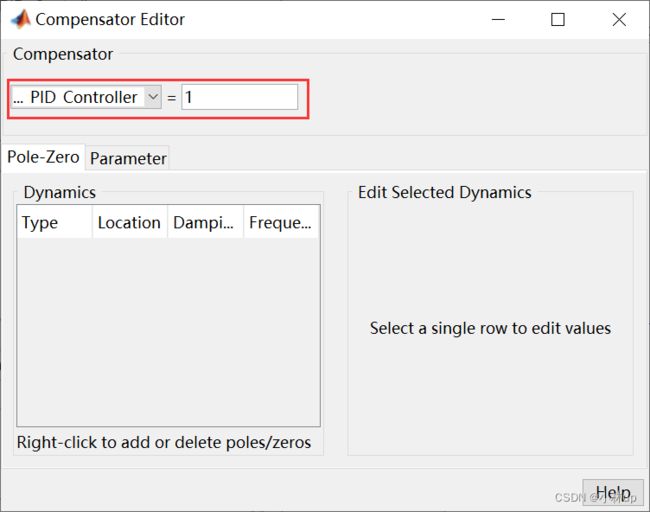
我们首先打开看一下我们的pid的传递函数，在Controllers And Fixed Blocks选择Open Selection
我们看到pid的传递函数是1，和我们的初始的设置是一样的。
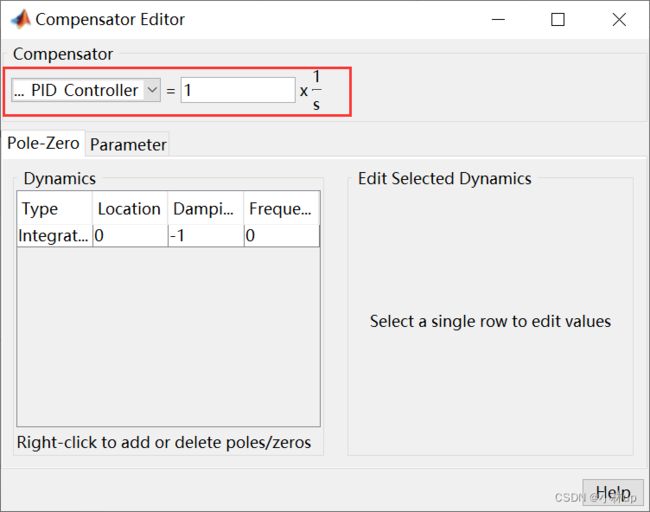
我们回到根轨迹图右键选中Add Porle or Zero，然后我们选中Integrator。
现在只有一个积分器，肯定是不稳定的，我们还要有个零点来组成PI控制器。
我们回到根轨迹图右键选中Add Porle or Zero，然后我们选中Real Zero。现在就是PI控制器了
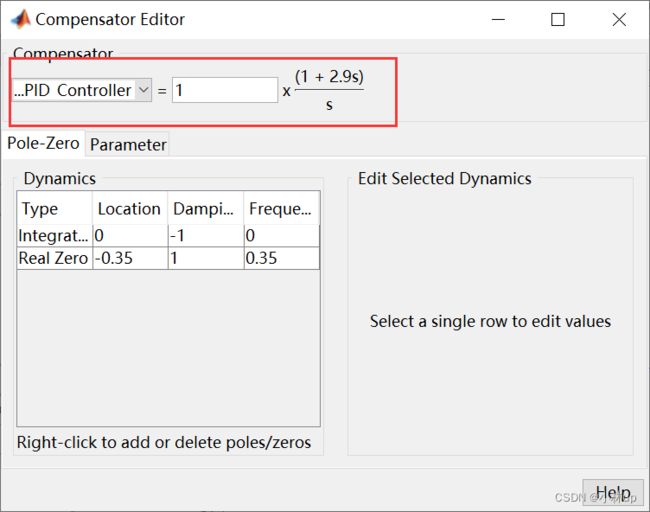
我们可以很方便地看PID三个参数的变化怎么影响输入输出曲线的（不同于直接的在PID控制器整定），我们选中Parameter，在下面有滑动条我们可以很方便地拖动调整最后的输出。在拖动的过程中输出曲线也会相应变化！
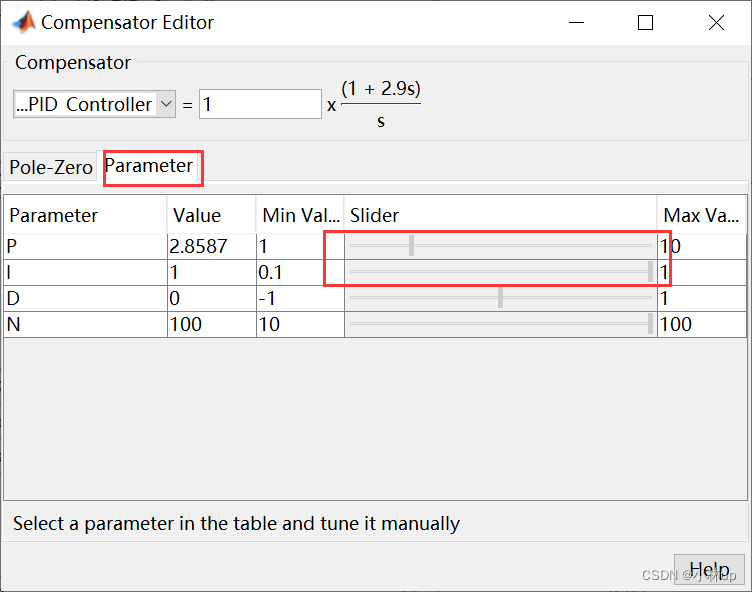
看看下面的gif。还是很方便的。
最后我们设置零点的位置是-0.15，如图所示最终的pid效果，传递函数为 0.5 × 1 + 6.7 s s 0.5\times \frac{1+6.7s}{s} 0.5×s1+6.7s
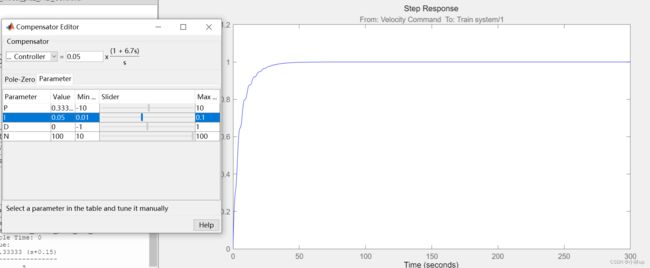
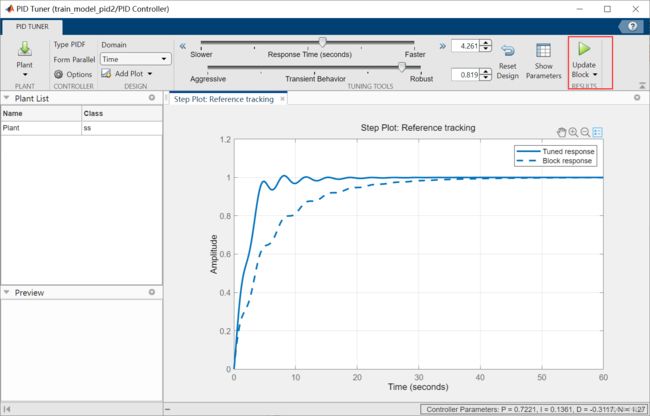
我们将调整好的pid参数更新到simulink模型里，点击菜单栏的Update Blocks。
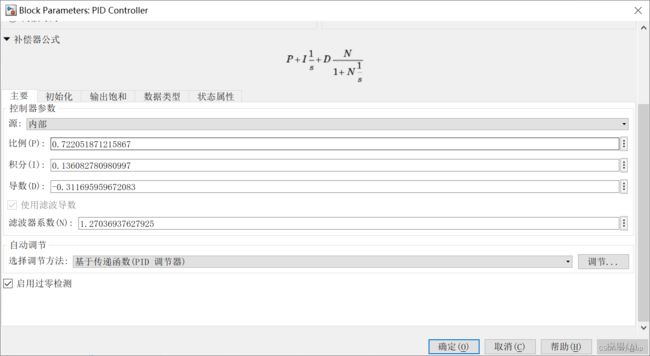
重新点击我们模型框图里的pid控制器，我们看到pid的参数确实改了。
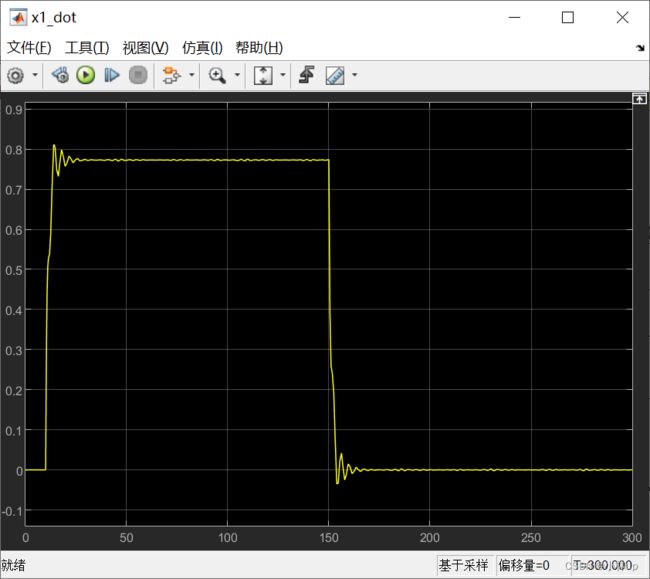
我们看到最终的效果就好很多了。速度很平稳地到了1，也没有发生超调。
这里在上面网站的基础上拓展一点：在pid控制器模块里也有整定参数的按钮：调节
滑动上面的滚动条也可以查看曲线，但是这就是pid控制器了，kd也会被考虑进来。
我们整定好也可以点击如图的Update Blocks
于是我们的pid参数又变了
运行一下再看下效果，响应速度变快了，但是就有一些跳变了，但是依旧没有超调：
