YOLO v8目标跟踪详细解读（二）
上一篇，结合代码，我们详细的介绍了YOLOV8目标跟踪的Pipeline。大家应该对跟踪的流程有了大致的了解，下面我们将对跟踪中出现的卡尔曼滤波进行解读。
1.卡尔曼滤波器介绍
卡尔曼滤波（kalman Filtering）是一种利用线性系统状态方程，通过系统输入观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。
卡尔曼滤波在测量方差已知的情况夏能够从一系列存在测量噪声的数据中，估计动态系统的状态。在目标跟踪中，将检测框的坐标看作观测数据，通过状态转移矩阵与状态协方差矩阵来更新下一帧的最优估计。
2.卡尔曼滤波器的基本概念
首先，我们需要了解卡尔曼滤波器的一些基本概念。 X k ^ \hat{X_k} Xk^表示k时可的状态量， F k F_k Fk表示 X k ^ \hat{X_k} Xk^的状态转移矩阵（运动估计矩阵）。我们可以利用 X k − 1 ^ \hat{X_{k-1}} Xk−1^通过 F k F_k Fk获得k时刻的估计 X k ^ \hat{X_k} Xk^。 P k P_k Pk作为状态协方差矩阵，也需要根据 F k F_k Fk更新。
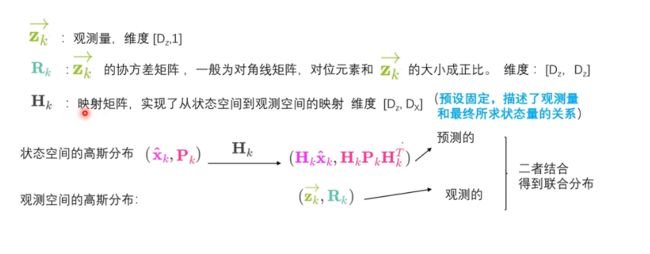观测量与状态量可能存在两个不同的空间，因此需要 H k H_k Hk实现状态空间到观测空间的映射。由于传感器检测的观测量存在误差，我们可以把观测空间理解为高斯分布，而状态量本就是一种估计，相较于观测量，状态量可以理解为具有较大方差的高斯分布，其均值为状态量。
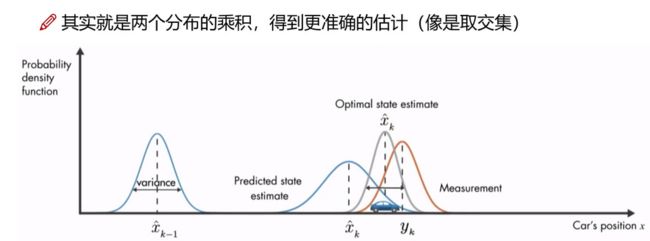如上图所示，状态量 X k − 1 ^ \hat{X_{k-1}} Xk−1^是位于左侧的高斯分布，通过状态转移矩阵获得k时刻状态量 X k ^ \hat{X_k} Xk^，由于过程中存在各种误差，方差较大。红色部分是k时刻的观测量 y k y_k yk。由于无法预知 X k ^ \hat{X_k} Xk^和 y k y_k yk两者哪边更为准确，我们将两者结合，得到的联合分布看作卡尔曼滤波最后更新的状态量。
已知两个高斯分布，其联合分布也为高斯分布，联合高斯分布的均值为 μ ^ ′ \hat{\mu}' μ^′, Σ ^ ′ \hat{\Sigma}' Σ^′。
根据上图中简单的矩阵计算，我们得到卡尔曼滤波预测与更新5个重要公式。
预测： P k − 1 P_{k-1} Pk−1, X k − 1 ^ \hat{X_{k-1}} Xk−1^根据状态转移矩阵获得k时刻 P k ^ \hat{P_{k}} Pk^与 X k ^ \hat{X_{k}} Xk^
更新：将状态量映射至观测量空间，联合观测量更新状态量 X k ^ ′ \hat{X_{k}}' Xk^′，状态协方差矩阵 P k ′ {P_{k}}' Pk′，本质是将观测量与状态量的高斯分布结合，形成的联合分布看作最终状态量的分布，其中 K ′ K' K′称为卡尔曼增益。
3.卡尔曼滤波在目标跟踪的应用
首先，状态量为[x,y,a,h,dx,dy,da,dh],我们需要预测坐标框下一帧的位置，所以状态转移矩阵很简单，表示为图中所示固定矩阵 F k F_k Fk。物理意义:下一时刻的位置=该时刻的位置+该时刻的速度× Δ \Delta Δt，这里 Δ \Delta Δt设为1。系统输入 u k u_k uk设为0。
为什么选用xyah作为状态量，而不是xyxy？主要考虑xyah作为4个独立变量，他们的协方差=0，因此协方差矩阵可以表示为对角矩阵。而xyxy形式，左上角坐标与右小角坐标有相关性，协方差矩阵不可表示为对角矩阵。
观测量为[x,y,a,h]，因此映射矩阵 H k H_k Hk为图中所示固定矩阵。我们对KF进行初始化，self._motion_mat表示 F k F_k Fk状态转移矩阵，self._update_mat表示 H k H_k Hk映射矩阵， self._std_weight_position表示位置方差的权重，self._std_weight_velocity 表示速度方差的权重，赋值均为经验值。
def __init__(self):
"""Initialize Kalman filter model matrices with motion and observation uncertainties."""
ndim, dt = 4, 1.
# Create Kalman filter model matrices.
self._motion_mat = np.eye(2 * ndim, 2 * ndim)
for i in range(ndim):
self._motion_mat[i, ndim + i] = dt
self._update_mat = np.eye(ndim, 2 * ndim)
# Motion and observation uncertainty are chosen relative to the current
# state estimate. These weights control the amount of uncertainty in
# the model. This is a bit hacky.
self._std_weight_position = 1. / 20
self._std_weight_velocity = 1. / 160
将该帧未关联的检测框坐标作为新轨迹的状态量，同时将mean_vel初始化为0。 X k ^ \hat{X_k} Xk^=mean = np.r_[mean_pos, mean_vel]。 P k {P_k} Pk初始化，其中x,y,h, x ′ , y ′ , h ′ x',y',h' x′,y′,h′的方差均与h为正比，a， a ′ a' a′为宽高比，方差为常值1e-2,1e-5。因为xy为检测框中心点，它存在于图中任意点，作为方差没有意义，因此方差正比于h。
def initiate(self, measurement):
"""Create track from unassociated measurement.
Parameters
----------
measurement : ndarray
Bounding box coordinates (x, y, a, h) with center position (x, y),
aspect ratio a, and height h.
Returns
-------
(ndarray, ndarray)
Returns the mean vector (8 dimensional) and covariance matrix (8x8
dimensional) of the new track. Unobserved velocities are initialized
to 0 mean.
"""
mean_pos = measurement
mean_vel = np.zeros_like(mean_pos)
mean = np.r_[mean_pos, mean_vel]
std = [
2 * self._std_weight_position * measurement[3], 2 * self._std_weight_position * measurement[3], 1e-2,
2 * self._std_weight_position * measurement[3], 10 * self._std_weight_velocity * measurement[3],
10 * self._std_weight_velocity * measurement[3], 1e-5, 10 * self._std_weight_velocity * measurement[3]]
covariance = np.diag(np.square(std))
return mean, covariance
在进行轨迹关联前，需要预测轨迹在该帧的状态量。上面我们已经讨论了卡尔曼滤波预测的公式，翻译成代码就如下所示，其中motion_cov表示不确定性干扰，通常为对角矩阵状态量相关，对位元素越大，其值越大。
def predict(self, mean, covariance):
"""Run Kalman filter prediction step.
Parameters
----------
mean : ndarray
The 8 dimensional mean vector of the object state at the previous
time step.
covariance : ndarray
The 8x8 dimensional covariance matrix of the object state at the
previous time step.
Returns
-------
(ndarray, ndarray)
Returns the mean vector and covariance matrix of the predicted
state. Unobserved velocities are initialized to 0 mean.
"""
std_pos = [
self._std_weight_position * mean[3], self._std_weight_position * mean[3], 1e-2,
self._std_weight_position * mean[3]]
std_vel = [
self._std_weight_velocity * mean[3], self._std_weight_velocity * mean[3], 1e-5,
self._std_weight_velocity * mean[3]]
motion_cov = np.diag(np.square(np.r_[std_pos, std_vel]))
# mean = np.dot(self._motion_mat, mean)
mean = np.dot(mean, self._motion_mat.T)
covariance = np.linalg.multi_dot((self._motion_mat, covariance, self._motion_mat.T)) + motion_cov
return mean, covariance
在更新状态量之前，需要将状态量以及状态协方差矩阵映射到观测量空间，公式如下所示。
def project(self, mean, covariance):
"""Project state distribution to measurement space.
Parameters
----------
mean : ndarray
The state's mean vector (8 dimensional array).
covariance : ndarray
The state's covariance matrix (8x8 dimensional).
Returns
-------
(ndarray, ndarray)
Returns the projected mean and covariance matrix of the given state
estimate.
"""
std = [
self._std_weight_position * mean[3], self._std_weight_position * mean[3], 1e-1,
self._std_weight_position * mean[3]]
innovation_cov = np.diag(np.square(std))
mean = np.dot(self._update_mat, mean)
covariance = np.linalg.multi_dot((self._update_mat, covariance, self._update_mat.T))
return mean, covariance + innovation_cov
最后，结合观测量，构建联合高斯分布，更新状态量。
def update(self, mean, covariance, measurement):
"""Run Kalman filter correction step.
Parameters
----------
mean : ndarray
The predicted state's mean vector (8 dimensional).
covariance : ndarray
The state's covariance matrix (8x8 dimensional).
measurement : ndarray
The 4 dimensional measurement vector (x, y, a, h), where (x, y)
is the center position, a the aspect ratio, and h the height of the
bounding box.
Returns
-------
(ndarray, ndarray)
Returns the measurement-corrected state distribution.
"""
projected_mean, projected_cov = self.project(mean, covariance)
chol_factor, lower = scipy.linalg.cho_factor(projected_cov, lower=True, check_finite=False)
kalman_gain = scipy.linalg.cho_solve((chol_factor, lower),
np.dot(covariance, self._update_mat.T).T,
check_finite=False).T
innovation = measurement - projected_mean
new_mean = mean + np.dot(innovation, kalman_gain.T)
new_covariance = covariance - np.linalg.multi_dot((kalman_gain, projected_cov, kalman_gain.T))
return new_mean, new_covariance