递归零知识证明
本文我们将介绍递归零知识证明(ZKP),即一个证明证明了另一个证明的有效性,以及它优于标准非递归零知识证明 (ZKP) 的优势,并通过将其应用于证明费拨那契 (Fibonacci) 序列来展示它的强大功能。
什么是递归 ZKP
假设 Peggy 想向 Victor 证明她下周将在公园度过,而她只想使用一张照片来证明这一点。她可以做到以下几点:
图1: 递归证明
第 1 天,她在公园里拍了一张照片,上面有显示日期的日历。
第 2 天,她拿着第 1 天的照片在公园里用日历拍了另一张照片。
第 3 天,她拿着日历在公园里拍了另一张照片,同时拿着第 2 天拍摄的照片。
重复相同的程序直到第 7 天。现在,她用一张照片证明了她为期一周的旅行。
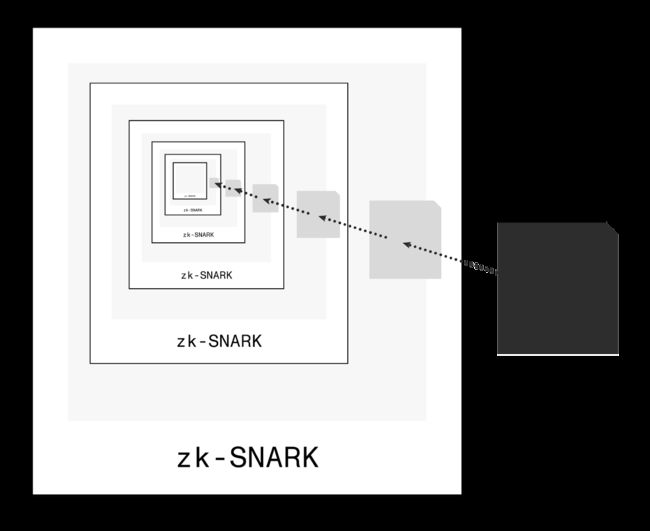
类似于上面的比喻示例,在递归 ZK 证明中,该证明证明了另一个证明的有效性,该证明本身也验证了另一个证明,依此类推。
为什么我们需要它
与标准 ZKP 相比,递归 ZKP 具有几个显着优势。
聚合
多个证明可以聚合成一个证明。单一证明只有在所有组成证明都有效时才有效,并且更容易验证。当在区块链上验证证明时,这尤其有吸引力。数以千计的证明可以压缩成一个证明,从而节省大量的验证成本。
图2: 多个证明合并为一个证明
并行化证明生成
假设我们要证明一批 1000 笔交易在 rollup 中是有效的。使用标准 ZKP,证明者需要为每笔交易生成一个单独的证明来依次验证 1000 笔交易,这是一项非常耗时的工作。所有证明都可以并行生成,因为它们都是独立的,因此证明时间要短得多。这些单独的交易证明可以递归地聚合在一个单一的证明中,如上所示。
增量可验证计算 (IVC)
如果证明是可增量更新的,那么证明某些类型的计算会更有效。
-
长计算:证明一个过长的计算会在证明者端占用大量内存。有些计算甚至无法放入内存中,因此无法证明。
-
演进计算:例如,我们想证明区块链的状态,但它在不断增长。我们计算一个新的证明,它不仅可以验证新块,还可以验证现有的证明本身。
我们将计算分解为更小的步骤并迭代地证明它们。每个步骤都包含一个证明,证明计算的当前状态。使用递归 ZKP(更具体地说,IVC),可以通过递归使用当前步骤及其证明来为下一步生成新证明。证明更新不需要像标准 ZKP 那样从第一步开始重新计算,并且与计算的总长度无关。
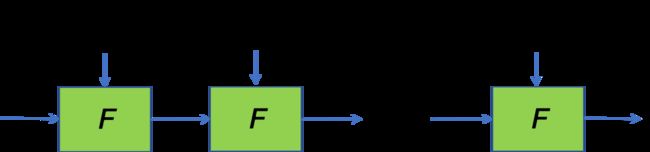
例如,对于 i 从 0 到 n 的函数 F,我们有以下计算:
zᵢ 是公共输入, wᵢ 是秘密输入(即见证人)。如果我们从 z₀ 开始,我们想要有效地证明最终输出是 zₙ。
IVC 通过生成初始证明 ₀(F 是证明者算法)并在每一步逐步更新它来实现这一点。例如,₂ 不仅证明了 F(z₁, w₁) = z₂,而且还证明了 ₁ 也是有效的。通过归纳,最后的 ₙ 证明所有中间步骤都是正确的。
图5: 增量可验证计算
它是如何工作的
在高层次上,诸如 SNARK 之类的 ZKP 可以验证任意计算。由于验证 SNARK 本身就是一种计算,因此 SNARK 可以验证其他 SNARK 证明。递归 SNARK 证明证明存在先前存在有效的证明。此计算/电路的证明证明了内部证明的有效性,该证明可能包括另一个证明。
图7: 验证者
到目前为止,我们已经解释了递归 SNARK 在理论上是如何工作的。在实践中,验证是一种密集计算,涉及繁重的密码学操作,例如双线性配对。必须采用许多新技术,例如椭圆曲线的循环,才能有效地工作。在这篇简短的博文中,我们不会详述这些实际问题。
斐波那契示例
我们将递归 SNARK 应用于斐波那契数列。斐波那契数列由递归关系定义:
Peggy 想要让 Victor 相信序列中有一个数字,比如 55 (F₁₀)。可以使用 snarkyjs,一种用于递归 SNARK 的 Typescript/Javascript 框架。
import { SelfProof, Field, ZkProgram, verify} from 'snarkyjs';
let FibonacciSequence = ZkProgram({
publicInput: Field,
methods: {
// those are our base cases that we start with - defined as:
// fib_0 = 0
// fib_1 = 1
// we need a proof associated with the base cases so we can recursively verify their correctness
fib0: {
privateInputs: [],
method(fib: Field) {
fib.assertEquals(Field.zero);
},
},
fib1: {
privateInputs: [],
method(fib: Field) {
fib.assertEquals(Field.one);
},
},
inductiveFib: {
privateInputs: [SelfProof, SelfProof],
method(fib: Field, fib1: SelfProof<Field>, fib2: SelfProof<Field>) {
// recursion below
fib1.verify();
fib2.verify();
let newFib = fib1.publicInput.add(fib2.publicInput);
fib.assertEquals(newFib);
},
},
},
});
console.log('compiling ..');
const { verificationKey } = await FibonacciSequence.compile();
console.log('compiling finished');
// proving: generating proof by doing the actual computation
let fib_n_2 = await FibonacciSequence.fib0(Field.zero);
let fib_n_1 = await FibonacciSequence.fib1(Field.one);
// following the formula fibn = fibn-1 + fibn-2
let fib_n;
// proving fib_N
const N = 10;
for (let n = 2; n <= N; n++) {
console.log(`working on fib_${n}..`);
let publicInput: Field = fib_n_1.publicInput.add(fib_n_2.publicInput);
fib_n = await FibonacciSequence.inductiveFib(
publicInput,
fib_n_1,
fib_n_2
);
fib_n_2 = fib_n_1;
fib_n_1 = fib_n;
console.log(`got fib_${n} = ${fib_n.publicInput.toString()}`);
}
// verifying: verifier only needs the latest proof fib_n
console.log('verify...');
let ok = await verify(fib_n, verificationKey);
console.log(`is ${fib_n.publicInput.toString()} in the sequence? ${ok}`);
第 3-38 行定义了递归证明。我们在第 11 行有基本案例 fib0,在第 18 行有 fib1。归纳案例从第 26 行开始。证明在第 31 行和第 32 行递归验证,表示只有当 Fₙ-₁ 和 Fₙ-2 的证明都有效时,Fₙ 的证明才有效,并遵循公式。
第 41 行编译电路并检索验证密钥。
Peggy 从第 44 行到第 64 行迭代生成证明。
Victor 使用验证密钥验证最终证明。值得注意的是,他只需要最终证明并在几秒钟内验证它,而不管第 50 行的序列索引 N 是多少。
在这个简单示例中,Victor 可能只是重新计算整个序列直到 N 为 10 并立即验证它。当 N 很大时,例如 1,000,000,000,000,递归 SNARK 的优势更加明显。Victor 仍然可以在几秒钟内验证证明,比重新计算要快得多。