传统人工智能中的三大问题
基于神经网络和大样本统计规律的深度学习越来越走入瓶颈,人工智能的发展越来越向基于符号推理和因果推理的传统人工智能回归。AI算法工程师不能把眼光仅仅局限在海量样本的统计规律上,而应该学习并掌握基于符号推理和小样本学习的传统人工智能技术。否则,当深度学习的热点一过,你很可能无法适应企业和市场对AI的新的需求。
本文介绍了传统人工智能要解决的三大问题:问题求解、博弈和谓词逻辑。它们都是基于符号推理和白盒推理的。了解相应的解决方案和算法有助于算法工程师开拓眼界,加深对算法本质的理解,增加解决问题、适应未来需求的能力。
1. 传统人工智能的三大问题
人工智能包括传统人工智能和现代人工智能两部分。机器学习、深度学习、遗传算法和强化学习是现代人工智能的主要分支。他们主要解决分类、回归、聚类、关联和生成等问题。而传统人工智能主要解决问题求解、博弈和谓词逻辑三大问题。
传统人工智能之所以重要是因为:
- 传统人工智能的算法比较成熟、可靠、有效。很多能够用传统人工智能解决的问题就不应该使用复杂且成本高昂的现代人工智能方法。比如求上海到北京之间的最短路径问题,用A*算法就要比深度神经元网络高效得多;
- 传统人工智能更基础。很多应用场景中,现代人工智能方法必须在传统人工智能基础上发挥作用。比如战胜围棋世界冠军李世石的AlphaGo其基础部分仍然是博弈算法,而残差神经元网络(深度学习技术之一)只不过在评价棋局优劣时发挥了作用。作为一个算法工程师,如果你只懂深度学习不懂博弈算法,是很难编写出高效的围棋程序的;
- 深度学习是基于黑盒推理的,往往知其然而不知其所以然。也就是说,它能解决问题,但是我们不知道它为什么能解决问题。而传统人工智能的各种算法一般都是基于白盒推理的,知其然更知其所以然;
- 更重要的是,我们不能以“有没有用”为标准来评价传统人工智能。就像数学中某些当时看来“没有用”的理论和方法一样,当它“有用”时你再去研究它就迟了。
2. 问题求解
2.1 状态和状态转化
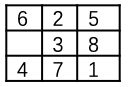
这里的问题是指可以用状态来描述的,且起始状态和终止状态明确的问题。比如,八数码问题的一个可能的起始状态如下图所示:
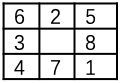
在一个3*3的网格中随机放置了1-8八个数码。其中有一个网格是空着的。这个空网格可以跟上下左右四个方向的任何一个临近的数码交换。但不能跟斜方向上的数码交换。比如上图中空网格可以和右边的那个数码3相交换,得到的子状态就是:
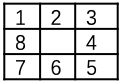
八数码问题就是研究如何用最少的次数移动空网格,从而使得八个数码最终呈现出如下所示的终止状态:
2.2 搜索树
问题求解的一个最简单的方法就是构造搜索树。方法是:
- 把初始状态看成是根结点,构成仅含有一个结点的搜索树T;
- 任选T中的一个候选结点a,把它的所有可能的子结点都挂在a之下。这个过程称为对a的扩展。所谓候选结点就是没有被扩展过的结点;
- 不断重复2)直到找到终止状态,或者没有候选结点为止。
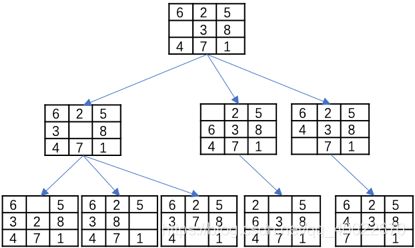
下图就是一个搜索树的例子(其中排除了重复的结点)。尽管上述算法并不能保证给出最少移动次数,甚至我们都不能保证它一定能终止(如果我们不排除重复结点的话),但是它仍然给出了问题求解算法的最基本框架。问题求解的各种算法(比如宽度优先、深度优先、爬山法、分支定界法和A*算法等)就是在这个框架基础上按照不同思路进行优化的结果。
比如宽度优先搜索,就是在算法的第2)步选择距离根结点最近的候选结点优先扩展。这个方法找到的第一个解一定也是最优解。所谓解就是从根结点到终止结点的一个路径。
所谓分支定界法就是在找到一个解之后,就把这个解的路径长度与以前找到的解的路径长度相比较,只保留路径短的那个。以后我们在扩展任何一个结点时,都要看看当前路径的长度是否短于解的路径长度。如果回答是“否“,则当前这个结点就没有必要扩展下去了。
至于其他更高明的算法,比如A*,这里就不再赘述。感兴趣的同学请关注方老师博客http://fanglin.blog.csdn.net。
与八数码问题类似的著名问题还有:
- 华容道问题:见上图,一个4*5的棋盘上有曹操、卒、马云、......大小不同的棋子。4个卒的大小都是1*1,黄忠、赵云、张飞和马超的大小是1*2,关羽的大小是2*1,曹操最大,大小是2*2。棋盘上还有两个1*1的空格以便棋子移动。游戏的目的是把曹操移到下方关口位置处,从而逃出华容道;
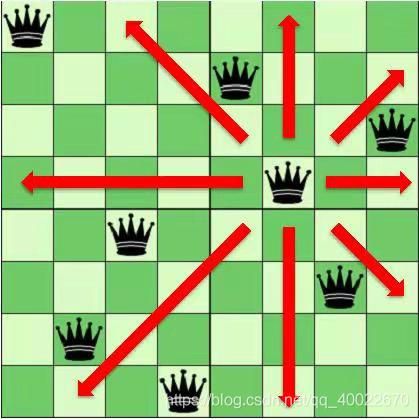
- 八皇后问题:在8*8的国际象棋棋盘上(见下图)如何放置八个皇后使得任意两个皇后都不在同一行、同一列或者同一斜线上;
- 求两个城市之间的最短路径问题;
- 背包问题:给定有限个物品以及每个物品的重量以及价值,比如罐头200克6元,手机125克5000元,等等。另外再给你一个最大负重为2000克的背包。问在不超过最大负重的情况下应该在背包中放置哪些物品从而获得最大的价值?
- 路径规划问题,怎样规划一个或者多个快递小哥的路径使得他们跑最少的路把一堆快递送到客户手中。这个问题还可以扩展到物流规划、船舶航运规划上。
八皇后问题
解决这些问题的关键在于如何描述问题的状态以及父状态如何生成子状态。比如最短路径问题中,状态就可以用当前所在的城市表示。城市与城市之间有道路直接连通的就可以构成父子状态的转换。由于道路一般是双向的,则父子状态的转换也是双向的。
而背包问题的状态可以用背包里当前所拥有的所有物品的集合表示。所谓子状态就是往父状态背包里添加任意一个不超重的物品构成的。
3. 博弈
3.1 博弈树
我们通常所说的博弈其实是博弈的最简单形式,即信息全透明的封闭环境下的两人零和博弈。围棋、象棋、国际象棋等都是这样的博弈。而扑克、麻将、多人跳棋等就不是。以下除非特指,所谓博弈都是指这种两人零和博弈。
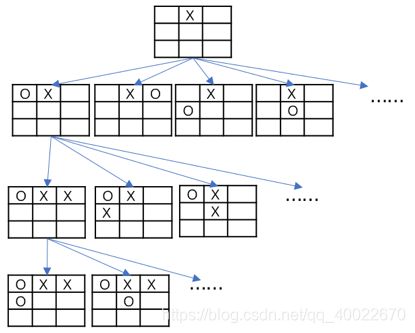
博弈要解决的问题是:当人类棋手下一步棋之后,电脑该如何应对呢?跟搜索树一样,博弈所采用算法也是从当前的根结点出发构建博弈树。以井字棋为例,井字棋是一种两人轮流在一个3*3的棋盘上下棋的游戏。目的是看谁先把自己的棋连成了一行、一列或者一条斜线。与中国的五子棋类似。以下是井字棋博弈树的部分结构:
井字棋的博弈树
与搜索树不同的是:
- 博弈树在扩展过程中,是双方轮流下棋的。而搜索树无需这样的考虑;
- 搜索树通常要考虑从根结点到当前结点的耗费,而A*算法甚至还要考虑从当前结点到可能的终止结点的预期耗费。耗费越小越好。而博弈树通常只考虑当前状态对双方的价值。价值越大越好,价值也称为得分。得分可以小于0(这表示对对方有利);
- 由于我们考虑的仅仅是两人零和博弈,所以当一个状态对一方的价值(或者说得分)是v的话,则同一个状态对另一方的价值就是-v;
- 如果某个状态下,当前走棋的一方已经获胜的话(比如井字棋中己方有三个棋子已经连成一条线),则他的得分就是正无穷大或接近无穷大,而另一方的得分就是负无穷大或接近负无穷大;
- 由于结点的数目会呈几何指数增加,所以博弈树和搜索树一样,都要解决组合爆炸问题。
3.2 简单博弈算法
简单博弈算法主要思想是:
- 博弈树上所有结点的得分都相对于当前下棋的一方计算。正得分表示对他有利,负得分表示对对方有利;
- 采用深度优先方法扩展候选结点。也就是说,优先扩展离根结点远的结点;
- 为了避免组合爆炸,当博弈树的高度达到一定高度h时,就停止扩展。此时当前结点的得分采用估算法或者深度学习方法获得。这个问题下面还要谈;
- 当一个结点的所有子结点的得分都确定之后,就可以确定该结点的得分。结点的得分总是等于所有子结点得分中最大得分的相反数。比如,假设所有子结点的得分分别是-3,12,7,-10,则当前结点的得分就是-12。这是因为,博弈算法假设对方是理性的,总是会走对他自己最有利的一步棋。而这一步的得分如果是v的话,对当前下棋的一方就是-v。因为是两人零和博弈嘛!有意思的是,这个方法也可以用来计算当前结点的父结点的得分。包括当前结点在内的所有兄弟节点中最大得分的相反数就是父结点的得分。所谓兄弟结点就是父结点相同的结点。这个过程可以不断地向上传播直到根结点;
- 根结点的所有子结点中得分最大的那个就是计算机的解。
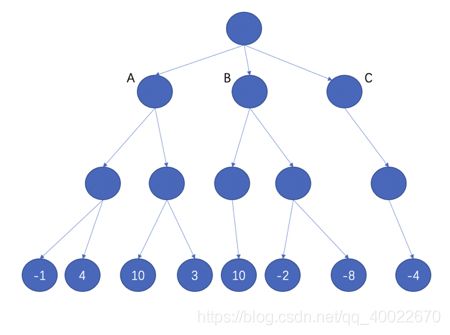
假设下图是一个限高4层的博弈树,其中所有叶子结点的得分都已经估算出来了:
博弈树(叶子结点的得分已被估算出来)
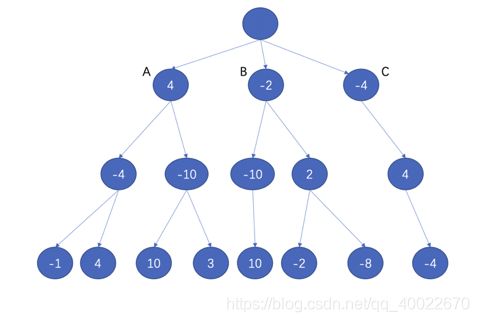
我们的问题是:A、B、C三个结点中,电脑会选择哪个下棋呢?我们只需沿着叶子结点向上,一层一层计算各个结点的得分即可。记住:每个非叶子结点的得分等于其所有子结点中最大得分的相反数。下面是计算结果:
从叶子结点出发向上一层层计算得分
根据上述结果我们显然知道,电脑应该选择结点A作为自己的应对。
3.3 估算得分
可能有人会问,我怎么估算结点的得分呢?这要看你们下的是什么棋。如果是井字棋,一般来说正中间的那个位置特别重要,谁占据了那个位置应该给谁高分。给多少分您就自己看着办吧。如果是象棋,可以计算一下双方的剩余棋力,比如“车”给100分,“兵”给1分。然后以双方的棋力差作为得分。这个方法没有考虑棋子的位置。其他棋类游戏都可以以此类推。
值得一提的是,深度学习方法可以在估算得分时发挥重要作用。AlphaGo等就是采用这个方法解决了围棋的组合爆炸问题。由于这个问题比较复杂,并且超出了本文的讨论范围,这里不再赘述。有兴趣的读者可以参考我以后的文章。
3.4 Alpha-Beta剪裁
绝大多数博弈游戏都面临组合爆炸问题。即随着结点的指数级扩展,博弈树的规模很快就达到天文数字。围棋的博弈程序就是基于这个原因才长期得不到解决直到引入深度学习方法。
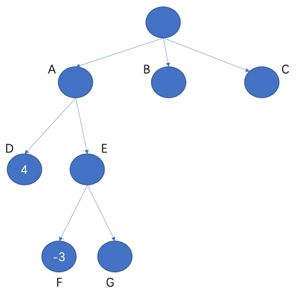
Alpha-Beta剪裁算法可以部分地解决这个问题。它的核心思想就是:如果当前结点的某个兄弟结点的得分是v,则当前结点的所有子结点的得分都必须小于-v。只要其中有一个子结点的得分大于或者等于-v,则当前结点及其以它为根结点的整个子树都可以从博弈树上删除。如下图:
Alpha-Beta剪裁示例
假设D的得分是4,E是D的兄弟结点。则E的子结点F和G的得分都必须小于-4。否则就应该把以E为根结点的子树从博弈树上删除。为什么呢?假设F的得分是-3,这意味着E和所有兄弟结点的最大得分至少是-3即:
max_value >= -3
前面我们讲过,E的得分应该等于-max_value。根据上面公式,我们得出E的得分必然小于等于3,从而小于D的得分4。这意味着我们根本就没有必要去扩展E的任何其他子结点了(比如G),因为即使扩展了G,E的得分也不会大于4。这就是Alpha-Beta剪裁的原理!
所以,使用Alpha-Beta剪裁算法时,博弈树的扩展常采用深度优先策略。这不仅更节省空间(因为没有必要保存整棵博弈树,只需把当前路径上的结点保存在一个堆栈中即可),更重要的是,深度优先策略有助于算法快速找到一个叶子结点,从而能把该结点的得分用来对相关结点进行剪裁。
关于Alpha-Beta剪裁的更多细节请关注方老师的博客。我在实践中使用这个方法实现了包括井字棋、五子棋、黑白棋等游戏的开发,证明了它的有效性。
4. 谓词逻辑
4.1 命题、谓词和规则
谓词逻辑主要研究如何进行逻辑推理。逻辑推理的基础是事实和规则。“张三和李四是朋友”,“ 太阳总是从东方升起”等就是事实。事实在谓词逻辑中是以命题的形式给出的。比如上述两个事实对应的命题分别是:
Is_Friend(“张三”,“李四”)
Rise_From(“Sun”,”Oriental”)
这里Is_Friends和Rise_From就是谓词,双引号扩起来的是字符串型逻辑常量。
规则形如:
If 条件 then 结论
其中条件和结论都是命题。比如:
If Is_Friend(X, Y) then Is_Friend(Y, X)
这个规则的含义是:如果X是Y的朋友,那么Y也是X的朋友。言下之意:朋友是相互的,不存在X是Y的朋友而Y却不是X朋友的情况。其中X和Y都是逻辑变量。
4.2 逻辑运算和复合命题
两个谓词之间可以用“and”或者“or”连接,分别表示“与”运算和“或”运算。比如,Is_Father(X, Y) and Is_Father(Y, Z)表示X是Y的父亲,Y是Z的父亲。这样由多个命题经过逻辑运算构成的命题称为复合命题。。
第三个逻辑运算是“not”,表示逻辑“非”操作。它是一个一元运算符。含义自明。
这样我们就可以用复合命题构成复杂的规则。比如:
If Is_Father(X, Y) and Is_Father(Y, Z) then Is_Grandpa(X, Z)
这个规则的意思是说:如果X是Y的父亲,Y是Z的父亲,则X是Z的爷爷。
4.3 自动逻辑推理
当我们把已知的命题和规则罗列在一起时,就能进行逻辑推理。逻辑推理的方法主要有两种,第一种是著名的三段式。比如,所有的猫都是哺乳动物,凯蒂是一只猫,所以凯蒂是哺乳动物。
第二种是利用规则进行反向推导。比如,假设我们想知道Tom的爷爷是谁。这实际上是求解命题Is_Grandpa(X, “Tom”)中X的值。怎么做呢?首先我们可以寻找所有结论是谓词Is_Grandpa的规则,这样的规则目前只有一条那就是:
If Is_Father(X, Y) and Is_Father(Y, Z) then Is_Grandpa(X, Z)
然后把Z=“Tom”代入其条件部分,则原命题Is_Grandpa(X, “Tom”)被替换为求解两个命题:
Is_Father(X,Y)and Is_Father(Y, “Tom”)
而求解这两个命题的方法是递归地调用上述步骤,直到所有命题都可以用三段式解决为止。
我们可以开发一个系统自动完成上述推理过程,这就是自动推理系统。事实上逻辑程序设计语言Prolog就是干这事的。如果你想自己开发一个这样的自动逻辑推理系统,你一定要注意:满足当前命题的规则可能不止一个,你应该在找到第一个答案前把所有可能的路径都走一遍而不是一旦一条路径走不通就下结论说原命题不成立。
递归显然不能满足这个要求,所以自动推理系统通常采用的是回溯法。如果你对如何构建自动推理系统感兴趣,请关注我以后的文章。
4.4 高阶谓词逻辑
我们前面所说的谓词逻辑实际是一阶谓词逻辑,也就是说,谓词的参数要么是变量,要么是常量。如果谓词的参数也是谓词,则这样的谓词就是二阶谓词。这已经超出了本文的讨论范围,本文不再赘述。
4.5 谓词逻辑的应用
谓词逻辑特别适合构建基于规则的专家系统、决策支持系统和规则系统。这与深度学习基于大量样本的黑盒推理完全不同。深度学习是从特殊(的样本)出发归纳出一般性的结论,谓词逻辑则是从一般性的规则出发推导出特殊情况下的结论,这是两个截然相反的过程。人脑就是这两个过程的完美结合体。
5. 结束语
本文简单介绍了传统人工智能的问题求解、博弈和谓词逻辑,目的是帮助非计算机专业的算法工程师开拓眼界增加认知的。要想了解更多的详情还需要你系统学习《人工智能》课程,或者关注我的博客。