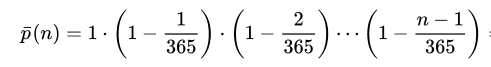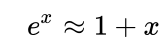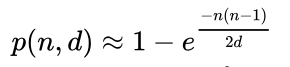【总结二】现代密码学

 【总结一】现代密码学_FansMing的博客-CSDN博客

目录

4 Hash函数

4.1 Hash函数满足条件及作用

4.2 哈希碰撞

4.2.1 生日攻击

 4.2.2 哈希碰撞公式（标记）

4.2.3 如何防止哈希碰撞

4.3 Hash函数的主要结构

4.3.1 Merkle-Damgård(MD)结构

4.3.2 海绵(Sponge)结构

4.4 Hash函数典型算法

4.4.1 SHA-256

4.4.2 SAH-3 Keccak

5 消息认证码

5.1 消息认证码的使用步骤

5.2 消息认证码的实例

5.2.1 SWIFT

5.2.2 IPsec

5.2.3 SSL/TLS

5.3 消息认证码的实现方法

5.3.1 认证加密

5.3.2 HMAC

5.4 对消息认证码的攻击

5.4.1 重放攻击

5.4.2 密钥推测攻击

5.5 消息认证码无法解决的问题

6 公钥密码

6.1 密钥配送问题

6.2 RSA

6.2.1 RSA算法过程

6.2.2 RSA算法的安全性

6.2.3 RSA算法的破解思路

6.3 ElGamal公钥密码

6.4 Rabin方式

6.5 椭圆曲线密码

7 数字签名

7.1 公钥密码与数字签名

7.1.2 RSA签名算法

7.1.3 ELGamal-签名

 7.1.4 DSS签名算法

7.2 对数字签名的攻击

7.3 证书

---

4 Hash函数

        Hash函数是将任意长的消息M映射为较短的、固定长度的一个值H(M),Hash函数也称为哈希函数、散列函数、压缩函数、杂凑函数、指纹函数等。其函数值H(M)为哈希值、散列值、杂凑码、指纹、消息摘要等。（Hash函数H一般是公开的）

4.1 Hash函数满足条件及作用

        Hash函数的目的是为需认证的数据产生一个“指纹”，为实现安全认证，需要满足以下安全条件：

单向性：已知x，求H(x)较为容易；但是，已知h，求使得H(x)=h的x在计算上是不可行的。

抗弱碰撞性：已知x，找出y使得H(y)=H(x)在计算上是不可行的。

抗强碰撞性：找出任意两个不同的输入x、y，使得H(y)=H(x)在计算上是不可行的。

Hash函数的作用：

Hash函数应用于消息认证

        消息认证是用来验证消息完整性的一种机制或服务，消息认证保证发送方和接收方的信息一致，通常还要保证发送方的身份真实有效。

Hash函数应用于数字签名
        消息认证通常用消息认证码（MAC）实现，即带密钥的Hash函数。数字签名与MAC相似，在进行数字签名过程中，用户的私钥加密消息作为Hash的输入，然后输出消息摘要，其他任何知道该用户公钥的人都可以通过数字签名来验证消息的完整性。攻击者只有获得了私钥，才能篡改消息。

Hash函数还可以用于产生单向口令文件，用于入侵检测和病毒检测，用于构建随机函数或者伪随机数发生器。

4.2 哈希碰撞

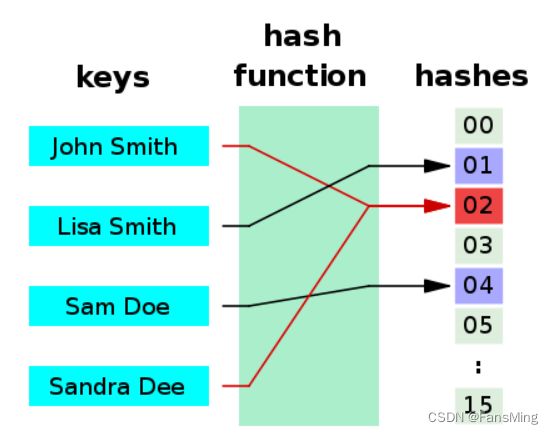
        所谓哈希，就是将不同的输入映射成独一无二的、固定长度的值（哈希值）。但当不同的输入得到了同一个哈希值，就发生了“哈希碰撞”。

         在很多网络服务中会使用哈希函数产生一个token，标识用户的身份和权限。但如果两个不同的用户得到了同样的token，就发生了哈希碰撞。而这意味着服务器把这用户A和用户B视为同个人，用户B可以读取和更改用户A的信息，这无疑是一个巨大的安全隐患。

        黑客攻击的一种方法，就是设法制造"哈希碰撞"，然后入侵系统，窃取信息。

4.2.1 生日攻击

        哈希碰撞的概率取决于两个因素（假设哈希函数是可靠的，每个值的生成概率都相同）

（1）取值空间的大小（即哈希值的长度）

（2）整个生命周期中，哈希值的计算次数

      数学上有一个问题，叫做"生日问题"（birthday problem）：一个班级需要有多少人，才能保证每个同学的生日都不一样？

        答案很出人意料。如果至少两个同学生日相同的概率不超过5%，那么这个班只能有7个人。事实上，一个23人的班级有50%的概率，至少两个同学生日相同；50人班级有97%的概率，70人的班级则是99.9%的概率（计算方法见后文）。

        这意味着，如果哈希值的取值空间是365，只要计算23个哈希值，就有50%的可能产生碰撞。也就是说，哈希碰撞的可能性，远比想象的高。实际上，有一个近似的公式。

        上面公式可以算出，50% 的哈希碰撞概率所需要的计算次数，N 表示哈希的取值空间。生日问题的 N 就是365，算出来是 23.9。这个公式告诉我们，哈希碰撞所需耗费的计算次数，跟取值空间的平方根是一个数量级。

        这种利用哈希空间不足够大，而制造碰撞的攻击方法，就被称为生日攻击（birthday attack）。

 4.2.2 哈希碰撞公式

        至少两个人生日相同的概率，可以先算出所有人生日互不相同的概率，再用 1 减去这个概率。我们把这个问题设想成，每个人排队依次进入一个房间。第一个进入房间的人，与房间里已有的人（0人），生日都不相同的概率是365/365；第二个进入房间的人，生日独一无二的概率是364/365；第三个人是363/365，以此类推。

        因此，所有人的生日都不相同的概率，就是下面的公式。

        上面公式的 n 表示进入房间的人数。可以看出，进入房间的人越多，生日互不相同的概率就越小。

        这个公式可以推导成下面的形式。

        那么，至少有两个人生日相同的概率，就是 1 减去上面的公式。

上面的公式，可以进一步推导成一般性的、便于计算的形式。

根据泰勒公式，指数函数 ex 可以用多项式展开。

如果 x 是一个极小的值，那么上面的公式近似等于下面的形式。

现在把生日问题的1/365代入。

因此，生日问题的概率公式，变成下面这样。

假设 d 为取值空间（生日问题里是 365），就得到了一般化公式。

上面就是哈希碰撞概率的公式。

4.2.3 如何防止哈希碰撞

        防止哈希碰撞的最有效方法，就是扩大哈希值的取值空间。

        16个二进制位的哈希值，产生碰撞的可能性是 65536 分之一。也就是说，如果有65537个用户，就一定会产生碰撞。哈希值的长度扩大到32个二进制位，碰撞的可能性就会下降到 4,294,967,296 分之一。

        更长的哈希值意味着更大的存储空间、更多的计算，将影响性能和成本。开发者必须做出抉择，在安全与成本之间找到平衡。

4.3 Hash函数的主要结构

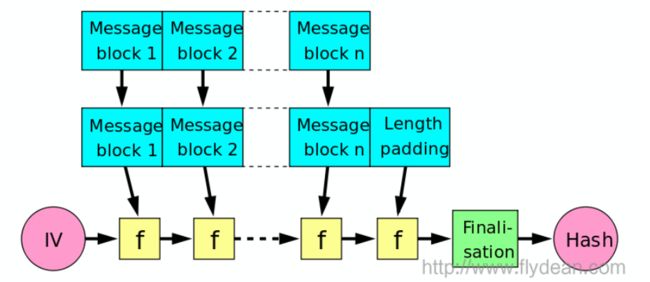
4.3.1 Merkle-Damgård(MD)结构

        Merkle–Damgård结构简称为MD结构，主要用在Hash算法中抵御碰撞攻击。这个结构是一些优秀的hash算法，比如MD5,SHA-1和SHA-2的基础。

        MD结构首先对输入消息进行填充，让消息变成固定长度的整数倍（比如512或者1024）。这是因为压缩算法是不能对任意长度的消息进行处理的，所以在处理之前必须进行填充。

        通常来说，我们会使用恒定的数据，比如说0来填充整个消息块。

MD结构流程图：

        举个例子，假如我们的消息是“HashInput”，压缩块的大小是8字节（64位），那么我们的消息将会被分成两个块，后面一个块使用0来填充，将会得到：“HashInpu t0000000”。

        但是这样做往往是不够的，因为通常对于压缩函数来说，会删除掉最后面的额外的0，所以导致填充和不填充最后计算出来的hash值是一样的。

        为避免这种情况，必须更改填充常量数据的第一位。由于常量填充通常由零组成，因此第一个填充位将强制更改为“ 1”。也就是“HashInpu t1000000”。

        我们还可以对填充进行进一步的增强，比如使用一个额外的block来填充消息的长度。 但是额外的使用一个block往往有点浪费，一个更加节约空间的做法就是，如果填充到最后一个block的0中有住够的空间的话，那么可以消息的长度放在那里。

4.3.2 海绵(Sponge)结构

        海绵结构，也称海绵哈希，是当前密码学中一种重要结构，如sha-3采用的是海绵结构。

        海绵结构是一类具有有限内部状态的算法，可以将任意有限长的输入消息变成任意长度输出的消息摘要，其结构如下

海绵结构主要分为两个部分：abaorbing和squeezing

在abaorbing过程中，f函数顺序迭代吸收消息，通常情况下，输入消息不是分组长度的整数倍，因此还要进行填充操作。

在squeezing过程中，根据输出长度来输出哈希值，每输出一个值，都要利用f函数来更新内部状态。

4.4 Hash函数典型算法

4.4.1 SHA-256

        SHA-256作为SHA-2(Secure Hash Algorithm 2，安全哈希算法2) 的一部分，目前已经是最流行的哈希算法之一。安全加密算法通过将输入文本拆分成独立的片段，并通过这些独立的片段生成最终的结果——加密算法哈希值。这些加密算法哈希值几乎是唯一的字符串，因而它们往往被用作数据块的摘要"digest"，指纹"figerprint"或签名"signature"。就比如说，SHA-256算法往往被用来生成256位的签名。

参考：https://blog.boot.dev/cryptography/how-sha-2-works-step-by-step-sha-256/

4.4.2 SAH-3 Keccak

        2012年10月，美国NIST选择了Keccak算法作为SHA - 3的标准算法，Keccak拥有良好的加密性能以及抗解密能力。

参考：https://blog.csdn.net/renq_654321/article/details/79797428

5 消息认证码

        在密码学中，消息认证码（Message authentication code，缩写为MAC），又名消息鉴别码、文件消息认证码、讯息鉴别码、信息认证码，是经过特定算法后产生的一小段信息，用作检查某段消息的完整性，以及作身份验证。它可以用来检查在消息传递过程中，其内容是否被更改过，同时可以确认消息的来源。

        消息认证码(MAC)也可以理解为与密钥相关联的单向散列函数。消息认证码和单项散列函数具有同样的性质，可以输入包括任意长度的消息，它就能输出固定长度的数据，这个数据就称为MAC值。

        消息认证码和Hash函数不同的是， 消息认证码的输入是信息+通信双方的共享验证码。其中共享密钥是完成认证工作；输入不同输出不同的性质是完成确定完整性工作，也就是确认消息是否被篡改。Hash函数与消息认证码在作用上也有区别：前者是确定消息是否被篡改，后者识别消息是否被伪装。

5.1 消息认证码的使用步骤

1.Alice与Bob事先共享密钥;

2.Alice根据汇款请求信息计算MAC值（使用共享密码）;

3.Alice将汇款请求消息和MAC值两者发送给接收者Bob;

4.Bob根据接收到的汇款请求消息计算MAC值（使用共享密钥）;

5.Bob将自己计算的MAC值与从Alice处收到的MAC值进行对比;

6.如果两个MAC值一致，则Bob就可以断定汇款请求的确来自Alice（认证成功）；如果不一致则说明不是来自Alice（认证失败）消息认证码的密钥配送问题;

        在消息认证码中，共享密钥起着重要作用，一旦被攻击者窃取，消息认证码的作用就失效了。实际上，对成密码的密钥配送问题在消息认证码中也同样会发生。因此，也可以采取同样的解决方案，通过公钥密码、Diffie-Hellman密钥交换、密钥分配中心等方式来解决配送问题。

5.2 消息认证码的实例

5.2.1 SWIFT

        SWIFT的全称是society for Worldwide Interbank Financial Telecommunication（环球银行金融电信协会），用于国际银行间的交易保驾护航。而银行间的通信就是使用的消息认证码，消息认证码使用的共享密钥则是由人来进行配送的

5.2.2 IPsec

        IPsec是对互联网基本通信协议-IP协议增加安全性的一种方式。在IPsec中，对通信内容的认证和完整性校验都是采用消息消息认证码来完成的。

5.2.3 SSL/TLS

        SSL/TLS对通信内容的认证和完整性校验也使用了消息认证码。

5.3 消息认证码的实现方法

5.3.1 认证加密

        认证加密是一种将对称密码与消息认证码相结合，同时满足机密性、完整性和认证三大功能的机制。
        Encrypt-then-MAC认证加密方式：先用对称密码将明文加密，然后计算密文的MAC值，通过MAC值就能判断明文的和密钥是否人为生成的，这可以避免发送任意伪造密文，让服务器解谜来套取信息的攻击。
        GCM认证加密方式：GCM中使用AES等128比特分组密码的CTR模式，并使用一个反复进行加法和乘法运算的散列函数来计算MAC值。由于CTR模式的本质是对递增的计算器值进行加密，因此可通过对若干分组进行并行处理来提高速度，CTR模式加密与MAC值的计算使用的是相同的密钥，因此管理也会更容易。专门用于消息认证码的GCM称为GMAC。

5.3.2 HMAC

        HMAC是一种使用单项散列函数来构造消息认证码的方法，其中受用的单向散列函数也并不仅限于一种。
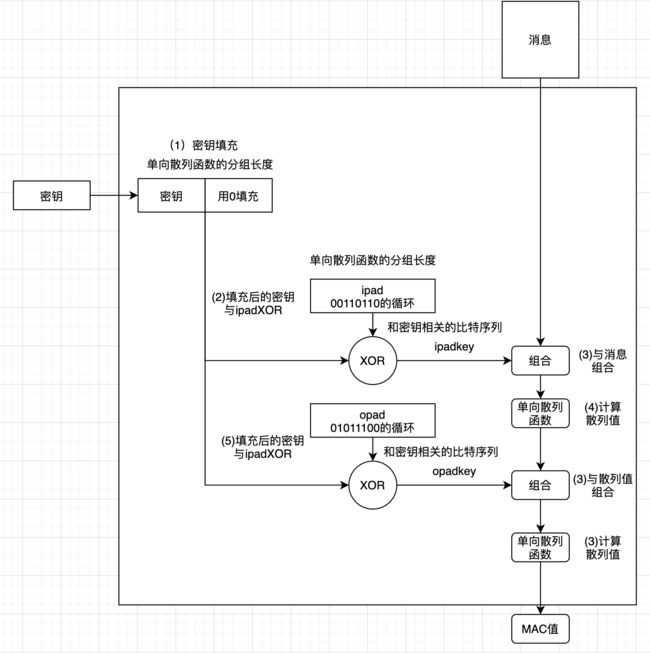
HMAC的步骤：

（1）密钥填充：

        如果密钥比单行散列函数的分组要短，就需要在末尾填充0，直到其长度达到单项散列函数的分组长度为止；如果超过长度，则使用单项散列函数求出密钥的散列值，将这个散列只用作HMAC的密钥

（2）填充后的密钥与ipad的异或运算

        将填充后的密钥与被称为ipad的比特序列进行XOR运算。ipad是将00110110这一比特序列不断循环往复直到达到分组长度所形成的比特序列。XOR运算所得到的值就是一个和单项散列函数的分组长度相同，且和密钥相关的比特序列，暂称为ipadkey。

（3）与消息组合，将ipadket附加在消息的开头

（4）计算散列值

（5）填充后的密钥与opad的异或运算

        将填充后的密钥与被称为opad的比特序列进行XOR运算。opad是将01011100这一比特序列不断循环往复直到达到分组长度所形成的比特序列。XOR运算所得到的值就是一个和单项散列函数的分组长度相同，且和密钥相关的比特序列，暂称为opadkey。

（6）与散列值组合

（7）计算散列值

最后得到的MAC值，一定是一个和输入的消息以及密钥都相关的长度固定的比特序列。

5.4 对消息认证码的攻击

5.4.1 重放攻击

        保存正确的MAC值不断重放来进行攻击，一次MAC使用多次交易，将导致巨额损失。

防御措施：

        序号：约定每次都对发送的消息赋予一个递增的编号，并且在计算MAC值时将序号也包含在消息中，这样攻击者因为无法计算出正确的MAC值将攻击失效。但是对每个通信对象都需要记录最后一个消息的序号。

        时间戳：约定在发送消息时包含当前的时间，如果收到以前的消息，即便MAC值正确也将其当作错误的消息来处理，这样就能够防御重放攻击。但是这要求发送者和接收者时间必须一致，否则会有延迟，留下重放攻击的空间

        nonce：通信前，接收者现象发送者发送一个一次性的随机数也就是nonce，将这个nonce包含在信息中并计算MAC值，因为每次都会发生变化，则避免了重放攻击，但是通信的数据量会增加。

5.4.2 密钥推测攻击

        因为消息认证码和单项散列函数类似，因此暴力破解和生日攻击同样有效。

        对于消息认证码而言，应保证不能根据MAC值推测出通信双方使用的密钥；以及在生成消息认证码所使用的密钥时，必须使用密码学安全的、高强度的伪随机数生成器。

5.5 消息认证码无法解决的问题

1.第三方证明

        因为使用的共享密钥，所以只有通信双方能证明是对方计算的MAC值，而无法向第三方证明是对方或自己计算的MAC值

2.防止否认

        双方使用共享密钥，可能会出现否认情况，又因为无法向第三方证明，因此使用消息认证码这完全取决于双方的信任程度。

参考: https://www.cnblogs.com/addc/p/16857822.html

6 公钥密码

        公钥密码是在20世纪70年代提出的，主要是为了解决密钥分配问题。公钥加密算法也称非对称密钥算法，用两对密钥：一个公共密钥和一个专用密钥。用户要保障专用密钥的安全；公共密钥则可以发布出去。公共密钥与专用密钥是有紧密关系的，用公共密钥加密的信息只能用专用密钥解密，反之亦然。由于公钥算法不需要联机密钥服务器，密钥分配协议简单，所以极大简化了密钥管理。除加密功能外，公钥系统还可以提供数字签名。

6.1 密钥配送问题

        在对称密码中，由于加密和解密的密钥是相同的，因此必须向接受者配送密钥。

        要使用对称密码进行解密，就必须使用和加密时相同的密钥才行，也就是只有同时将密钥也发送给Bob，Bob才能够完成解密，但是如果将密钥一同发送，窃听者Eve截获后也能够完成解密。因此，如果将密文和密钥同时发送时，则加密无效。

        解决配送问题的方法有：通过事先共享密钥、密钥分配中心、Diffie-Hellman、公钥密码四种方法来解决。

通过公钥密码来解决密钥配送问题

        在公钥密码中，加密密钥和解密密钥是不同的。只要拥有公钥密码，任何人都可以进行加密，但没有解密密钥是无法解密的。因此只有拥有解密密钥的人才能够进行解密

公钥通信的流程

1）Bob生成一个包含公钥和私钥的密钥对，私钥由Bob自行妥善保管；

2）Bob将自己的公钥发送给Alice，Bob的公钥被窃听者Eve截获也没关系，将公钥发送给Alice，表示Bob请Alice用这个公钥对消息进行加密并发送给他；

3）Alice用Bob的公钥对消息进行加密，加密后的消息只有用Bob的私钥才能够解密，虽然Alice拥有Bob的公钥，但用Bob的公钥是无法对密文进行解密的；

4）Alice将密文发送给Bob，密文被窃听者Eve截获也没关系。Eve可能拥有Bob的公钥，但是用Bob的公钥是无法进行解密的；

5）Bob用自己的私钥对密文进行解密。
通信流程图：

6.2 RSA

        RSA是一种公钥密码算法。由三位开发者（Rivest Shamir Adleman）三位开发，并取其名字首字母命名。RSA是一种使用不同的加密密钥与解密密钥，“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制。

        RSA公开密钥密码体制的原理是：根据数论，寻求两个大素数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

6.2.1 RSA算法过程

RSA加密

        在RSA中，明文、密钥和密文都是数字。
        加密公式：密文 = 明文E mod N （RSA加密）
        可以理解为明文和自己做E次乘法，然后将其结果处以N求余数，这个余数就是密文。因RSA的加密是求明文的E次方modN，所以只要知道E和N这两个数，任何人都可以完成加密的运算，所以E和N是RSA加密的密钥，组合起来也就是公钥。E和N合并在一起统称为公钥，因此表示时记作公钥（E，N）

RSA解密

        解密公式：明文 = 密文DmodN
        可以理解为将密文和自己做D次乘法，再对其结果除以N求余数就能得到明文。解密时用到的数字N和加密时用的数字N是相同的。数D和数N组合起来就是RSA的解密密钥，因此D和N的组合就是私钥。只有同时知道D和N两个数的人才能够完成解密的运算。

生成密钥对

        在整个过程中需要使用E、D、N三个数，其中E和N是公钥，D和N是私钥，因此求E、D和N这三个数就是生成密钥对。RSA密钥对的生成步骤如下：

1）求N
        首先需要准备两个很大的质数p和q，其中p和q太晓得话，密码会很容易被破译，但太大计算时间又会变得很长，如果p和q的大小都是512比特，相当于155位十进制数字。要求出这样大的质数，需要通过为随机数生成器生成一个512比特大小的数，再判断这个数是不是质数。如果伪随机数生成器生成的数不是质数，则需要重新生成。
        判断一个数是不是质数并不是看它能不能分解质因数，而是通过数学上的判断方法来完成（费马测试和米勒·拉宾测试）

2）求L（L是尽在生成密钥对的过程中使用的数）
        L这个数载RSA的加密和解密过程中都不会出现，他只出现在生成密钥对的过程中。L是p-1和q-1的最小公倍数(lcm)，如果lcm(X,Y)来表示"X和Y的最小公倍数"，则L：L = lcm（p-1，q-1）（L是p-1和q-1的最小公倍数）

3）求E
        E是一个比1大、比L小的数。此外，E和L的最大公约数(gcd)必须为1.如果用gcd(X,Y)来表示X和Y的最大公约数，则E和L之间存在关系：1 < E < L、gcd(E，L) = 1 (E和L的最大公约数为1，即互质)。而要加上E和L的最大公约数为1这个条件，是为了保证一定存在解密时需要使用的数D

4）求D
        数D是由数E计算得到的，D、E和L之间必须具备条件：1 < D < L、E * D mod L = 1。只要数D满足上述条件，则通过E和N进行加密的密文，就可以通过D和N进行解密。条件的D，就需要保证E和L的最大公约数是1，也正是对E的要求条件。

6.2.2 RSA算法的安全性

        RSA的安全性依赖于大数分解，但是否等同于大数分解一直未能得到理论上的证明，也并没有从理论上证明破译。RSA的难度与大数分解难度等价。因为没有证明破解RSA就一定需要做大数分解。假设存在一种无须分解大数的算法，那它肯定可以修改成为大数分解算法，即RSA的重大缺陷是无法从理论上把握它的保密性能如何，而且密码学界多数人士倾向于因子分解不是NPC问题。

6.2.3 RSA算法的破解思路

通过密文来求得明文
        公式中如果不加mod，知道E和N是能够很快推出明文的，因为就是一个求对数的问题。而加上mod N之后，就是求离散对数的问题

通过暴力破解来找出D
        找出D，能够通过暴力破解法来撞出密码，但是破解的难度也会随着D的长度增加二变大，当D足够大时，就不能在现实时间内通过暴力找出数D。目前RSA中所使用的p和q的长度都是1024比特以上，N的长度为2048比特以上。由于E和D的长度可以和N差不多，因此要找出D，就需要进行2048比特以上的暴力破解，这是很难实现的。

通过E和N求出D
        E和N都是由质数p和q推算出来的，质数p和q不被密码破译者知道，则无法通过此方法破译。也就是说将p和q交给密码破译者与吧私钥交给密码破译者是等价的。

对N进行质因子分解攻击
        因为N是公开的，但是由于p和q都是质数就只能通过对N进行质因子分解才能获得，因此一旦发现了对大整数进行质因子分解的高效算法，RSA就能够被破译

通过推测p和q进行攻击
        因为p和q都是根据伪随机数生成器生成，因此要选择可靠性高的伪随机数生成器，否则会被猜出破译

中间人攻击
        中间人攻击不破译RSA，而是针对机密性的有效攻击。整个过程符合流程，但是就因为攻击者的截获，误传信息，导致两人通信失败。因此为避免这种情况加入了证书机制。

选择密文攻击
        假设攻击者可以使用解密提示服务，发送任意数据，服务器都会将其当作密文来解密并返回解密的结果。因此通过RSA-OAEP在明文前面填充一些认证信息，如果解密时在数据的开头没找到正确的认证信息，就会返回错误信息，而不将错误内容返回。

6.3 ElGamal公钥密码

        该方式利用了mod N下求离散对数的苦难度，但是有一个缺点，经过加密的密文长度会变为明文的两倍。

6.4 Rabin方式

        Rabin方式利用了mod N下求平方根的困难度。因此破解Rabin等于破解RSA的质数因子难度。Rabin算法是一种基于模平方和模平方根的非对称加密算法。

参考：https://blog.csdn.net/Sway_F/article/details/109074460

6.5 椭圆曲线密码

        椭圆曲线算法(Elliptic Curve Cryptography,ECC)是基于椭圆曲线数学的一种公钥密码算法,其安全性依赖于椭圆曲线离散对数问题的困难性。

参考：https://zhuanlan.zhihu.com/p/443011441

7 数字签名

        数字签名（又称公钥数字签名）是只有信息的发送者才能产生的别人无法伪造的一段数字串，这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。它是一种类似写在纸上的普通的物理签名，但是在使用了公钥加密领域的技术来实现的，用于鉴别数字信息的方法。一套数字签名通常定义两种互补的运算，一个用于签名，另一个用于验证。数字签名是非对称密钥加密技术与数字摘要技术的应用。

7.1 公钥密码与数字签名

        公钥密码包括一个由公钥和私钥组成的密钥对，公钥用于加密，私钥用于解密

        数字签名中也同样会使用公钥和私钥组成的密钥对，不过这两个密钥的用法和公钥密码是相反的，即用私钥加密相当于生成签名，而用公钥解密相当于验证签名。

从消息认证码到数字签名
        消息认证码的局限性：因为使用了共享密钥的缘故，消息认证码无法防止否认。
        数字签名解决问题：Alice和Bob各自使用不同的密钥，只有本人知道的密钥，也就是数字签名

7.1.1 签名的生成和验证
        生成消息签名：由消息发送者对消息进行签名，也就是使用密钥对消息生成MAC值。整个过程可以理解为“我认可该消息的内容”
        验证数字签名：验证可以由消息接收方或者第三方完成，验证结果成功则代表签名确实属于发送者，失败则意味不属于发送者。
        数字签名对签名密钥和验证密钥进行了区分，使用验证密钥是无法生成签名的。签名密钥只能由签名的人持有，而验证密钥则是任何需要验证签名的人都可以持有。从这里来看和公钥密码的原理很类似，实际上，数字签名就是通过将公钥密码“反过来用”实现的。他们的关系如下：

        用公钥加密所得到的密文，只能用与该公钥配对的私钥才能解密；同样地，用私钥加密所得到的密文，也只能与该私钥配对的公钥才能解密。用私钥进行加密这一行为只能由持有私钥的人完成，正是基于这一事实才能够将私钥加密的密文作为签名来对待。

由于公钥是对外公开的，因此任何人都能够用公钥进行解密，于是任何人都能够对签名进行验证。

数字签名的方法
        直接对消息签名的方法：发送者用自己的私钥对消息进行加密 ；发送者将消息和签名发送给Bob ；接收者用发送者的公钥对收到的签名进行解密 ；接收者将签名解密后得到的消息与接收者直接发送的消息进行对比
        对消息的散列值签名的方法：发送者用单项散列函数计算消息的散列值；发送者用自己的私钥对散列值进行加密；发送者将消息和签名发送给接收者；接收者将签名解密后得到的散列值与发送者直接发送的消息的散列值进行对比。

        在实际使用场景中，人们更倾向于第二种方法。

7.1.2 RSA签名算法

密钥生成：

 签名算法：

 验证算法：

 RSA签名算法的缺点：

7.1.3 ELGamal-签名

 7.1.4 DSS签名算法

        1991年，数字签名标准（DSS）在ELGamal数字签名和Schnorr数字签名的基础上发展而来，被美国国家标准局(NIST)确定为数字签名标准。

密钥生成：

 签名算法：

 验证算法：

 DSS签名的正确性:

7.2 对数字签名的攻击

中间人攻击：

        攻击者对发送者伪装成接收者，对接收者伪装成发送者，这样可以在完全不用破解数字签名的前提下完成攻击。防御措施是：通信双方事先沟通确定双方的地址正确。

对单向散列函数的攻击：

        数字签名中所使用的单项散列函数必须具有强抗碰撞性，否则会生出另外一条不同的消息，使其与签名所绑定的消息具有相同的散列值。

利用数字签名攻击公钥密码：

        通过社会工程学，让使用者在不知情的情况下对未知消息进行签名。防御措施是：不对陌生和意思不清晰的消息进行签名

潜在伪造：

        签名的对象是无意义的消息（例如随机比特序列），如果攻击者能够生成合法的数字签名（即攻击者生成的签名能够正常通过校验），这称之为潜在威胁。防御措施是：在改良RSA的基础上开发了一种签名算法，叫作RSA-PSS，它并不是对消息本身进行签名，而是对其散列值进行签名。同时为了提高安全性，在计算散列值的时候还要对消息加盐。

其他攻击：

        对公钥密码的攻击大部分也适用于数字签名。

        要正确使用数字签名，有一个重要前提是，用于签名的公钥必须属于真正的发送者。因此为了确认得到的公钥是否合法，需要使用证书。

7.3 证书

        公钥证书类似于驾照等，由认证机构(AC)对其进行数字签名，只要看到公钥证书，就可以确认该公钥确实是其本人。公钥证书也简称为证书。

流程图：

（1）Bob生成密钥对
（2）Bob在认证机构Trent注册自己的公司
（3）认证机构Trent用自己的私钥对BOb的公钥施加数字签名并生成证书
（4）Alice得到带有认证机构Trent的数字签名的Bob的公钥（证书）
（5）Alice得到带有认证机构Trent的数字签名，确认Bob的公钥的合法性
（6）Alice用Bob的公钥加密消息并发送给Bob
（7）Bob用自己的私钥解密密文得到Alice的消息

公钥基础设施（PKI)
公钥基础设施是为了能够更有效地运用公钥而制定的一系列规范和规格的总称。其中PKI的组成要素分为：用户（使用KPI的人）、认证机构（颁发证书的实体）、仓库（保存证书的数据库）

对证书的攻击
证书就是用的数字签名技术，因此对数字签名的攻击适用于证书
1、在公钥注册之前进行攻击。在认证机构和Bob完成认证前，更改认证的公钥
2、注册相似人名攻击。更改用户信息的大小写或创建前面和后面的数字相同的公钥，利用人的惯性思维
3、窃取认证机构的私钥进行攻击。窃取认证机构的私钥，这就要求认证机构在私钥丢失的第一时间通知用户
4、伪装成认证机构进行攻击。如果认证机构本身不可信，即便证书合约，其中的公钥也不能使用
5、钻CRL的空子进行攻击。从公钥失效到接受者收到证书作废清单（CRL）需要一段时间，主动攻击者可以利用CRL发布的时间差来发动攻击。这就要求公钥失效时要尽快通知认证机构，及时发布和更新CRL
6、另一种钻CRL的空子进行攻击。交易的一方以私钥被盗为由，否认交易。这是需要外部能力的介入，或采用OCSP的协议