A Glance at Secure Multiparty Computation for Privacy Preserving Data Mining论文总结

Privacy Preserving Data Mining论文总结)

---

Abstract

概述了安全多方计算 (SMC) 的新兴研究领域。
提出了几个现有的以及新的 SMC 问题以及一些解决方案

SMC 字面意思是：
安全——对各个组织的数据安全和完整性的安全问题。
多方 - 涉及多个组织/各方进行隐私保护数据挖掘 (PPDM)。
计算 - 任何全局操作。
因此，将它们放在一起，这是一种提供多个组织的协作计算而不泄露单个组织的数据的机制。

Keywords: Privacy, Security, Trusted Third Party, Secure Multiparty Computation.
2009

---

I. INTRODUCTION

SMC 是一种隐私保护数据挖掘机制，用于网络环境中的联合计算。
它可以定义为以安全或可靠的方式在多个不同的组织之间提供计算。
使用 SMC，多方可以共同对其私有数据执行一些全局计算，而不会损失任何数据安全/隐私。它为端到端的安全多方协议开发提供了基础。

如果 D1,…, Dn 是对应于 n 个组织的数据，令 Di 是对应于第 i 个组织的数据组织，那么计算需要 Di 不应该被任何 Dj 访问，其中 i≠j 和 j=1, 2…n。
因此，每个组织只获得联合计算的最终结果，而不知道所涉及的输入和进行的计算。

例如，考虑一个病人在过去 5 年里一直生病。他接受了几位医生的治疗，有时他也住院了。如果我们希望计算该患者的完全康复时间，它将是患者从每个医生那里接受治疗的持续时间和他住院的持续时间的联合总和。每个医生和医院都维护着患者的数据库。现在这里涉及联合计算，该计算仅提供恢复持续时间，而不会泄露任何医生诊所或医院数据库的其他信息。

最简单和最通用的方法是在执行所有联合计算并维护安全性的所有组织之上使用可信第三方 (TTP)。

SMC 协议可能基于以下两种范式中的任何一种[12]：

• Real Model: 组织运行和使用自己的 SMC 协议，无需受信任的第三方。
• Ideal model: 组织依赖受信任的第三方进行计算。

1. Literature Survey

为了在互不信任的实体之间提供安全的联合计算，SMC已经做了大量的工作。 这种计算可以是选择性信息共享、算术/关系操作、排序、搜索、散列或其他类似操作。

SMC提供了一个转换框架，该框架系统地将正常计算转换为SMC计算。
根据可区分输入的个数，我们可以将计算分为单输入和多输入计算模型。
这一优点也可以被看作是一个缺点，因为所有的计算可能不一定要求相同的安全级别。 因此，有必要区分正常计算和SMC。 这样，所有的计算就不会招致相同的开销。 只有SMC问题才会产生开销，其他计算才能正常进行.

如果遵守引用的局部性，则需要反复请求一些结果以供进一步计算，缓存这些数据可以大大提高性能，但不能妨碍我们的安全考虑。

2. SMC problems

SMC可以以数据库查询、授权或认证验证、数学/关系计算、科学计算、统计计算或任何几何操作的形式进行。

3.1 Privacy Preserving Co-operative Scientific Computations

保护私隐的合作科学计算

• Linear System of Equations:线性方程组： 设Alice有m个私有线性方程组，表示为m1x=b1，而Bob有(NM)个私有线性方程组，表示为m2x=b2，其中x是n维向量。 爱丽丝和鲍勃希望共同找到一个能同时满足爱丽丝和鲍勃方程的向量“x”。

• Linear Least Square Problem:线性最小二乘问题： 设Alice有M1个私有线性方程组，用M1X=B1表示，Bob有M2个私有线性方程组，用M2X=B2表示，其中“X”是n维向量，M1+M2>n。 由于要满足的条件比自由度多，因此有可能违反其中的一些条件。 因此，我们取残差因子r，使r尽可能保持最小。 最小二乘准则是利用欧几里得（最小二乘）范数来确定R的大小。

• Linear Programming Problem:线性规划问题： 设Alice的私有线性方程组表示为M1X<=B1，而Bob的私有线性方程组表示为M2X<=B2，其中Alice的系统中有M1个线性方程组，Bob的系统中有M2个线性方程组。 我们想最小化a1x1+……。 +anxn对于已知的a1…an和解x=(x1…xn)应该满足Alice和Bob的要求。

这些问题通常被视为路由、计划、调度、分配、设计等。

3.2. Privacy Preserving Database Query:

• Database Query:数据库查询： 假设Alice想在Bob的字符串数据库S={S1，…，SN}中搜索一个字符串Q，它只想返回结果，而不显示Bob的整个字符串数据库。 匹配可以是精确匹配或近似匹配。

3.3. Privacy Preserving Intrusion Detection:

隐私保护入侵检测

• Profile Matching:配置文件匹配： 爱丽丝有一个黑客的配置文件数据库。 鲍勃最近追踪到一个人的行为，他怀疑他是黑客。 现在，如果鲍勃想检查他的怀疑是否正确，他需要检查爱丽丝的数据库。 爱丽丝的数据库需要保护，因为里面包含黑客的相关敏感信息。 因此，当鲍勃输入黑客的行为并搜索爱丽丝的数据库时，他无法查看他的整个数据库，取而代之的是，只得到匹配行为的比较结果。

• Fraud Detection:欺诈检测： 两个主要的金融组织希望在不共享数据模式的情况下合作防止对其计算系统的欺诈性入侵，因为它们各自的私人数据库包含敏感数据。

3.4: Privacy Preserving Data Mining:

隐私保护数据挖掘：

• Classification分类: Alice有一个私有数据库D1，而Bob有一个私有数据库D2。 Alice和Bob如何在不向对方透露私有数据库内容的情况下，建立基于D1∪D2的决策树？ ID3算法、增益比算法、Gini指数算法和SMC协议都可以用于决策树算法。
• Data Clustering:数据集群： Alice有一个私有数据库D1，而Bob有一个私有数据库D2。 Alice和Bob想在D1∪D2上联合进行数据聚类。 这主要是基于数据聚类原则，该原则试图增加内部相似性和最小化类间相似性。
• Mining Association Rules:挖掘关联规则： 让Alice有一个私有数据库D1，让Bob有一个私有数据库D2。 如果Alice和Bob希望在不泄露单个数据库信息的情况下，从D1∪D2中联合寻找关联规则。
• Data Generalization, Summarization and Characterization:数据概括、总结和表征： 让Alice有一个私有数据库D1，让Bob有一个私有数据库D2。 如果他们希望对其组合数据库D1∪D2联合进行数据概括、总结或表征，则该问题成为SMC问题。

3.5. Privacy Preserving Geometric Computation:

隐私保护几何计算；

• Intersection:交集： 让Alice有一个私有的形状A，让Bob有一个私有的形状B，如果Alice和Bob想要找到A和B是否相交，那么他们需要共享他们的形状坐标数据库来找到他们是否相交
• Point Inclusion Problem:点包含问题： 设Alice有私有形状A，而Bob有私有点P。 现在，如果Bob想知道他的私有点P是在形状边界上还是在内部还是外部，那么他们需要共同使用这两个数据库，而不向对方透露他们各自的信息。
• Range Searching:范围搜索： 让Alice有一个私人范围，Bob有N个私人点。 爱丽丝和鲍勃想共同寻找爱丽丝范围内的点数； 两人都不愿意向另一方透露他们的数据。
• Closest Pair:最近对： 设Alice在平面上有m个私有点，Bob在平面上有n个私有点。 Alice和Bob想联合寻找(m+n)点中最近的两点，即相互距离最小的两点。
• Convex Hull:凸包： Alice和Bob在一个平面上分别有m个私有点和n个私有点。 他们希望从这些(m+n)点找到一个凸包。

3.6. Privacy Preserving Statistical Analysis:

隐私保护统计分析：

Correlation and Regression:相关和回归： 设D1=(x1，…，xn)是Alice的私有数据集，D2=(y1，…，yn)是Bob的私有数据集。 Alice和Bob希望共同找到以下结果：

• x和y之间的相关系数：在私有数据集D1和D2之间找到相关系数，而不会相互透露D1或D2。
• 回归线：这有助于找到D1和D2的回归线，并为未来的预测执行回归分析。

3.7.Selection Problem:

选择问题： 让爱丽丝和鲍勃拥有自己的私人数据库。 如果他们希望在对方的数据库上应用任何选择程序，那么这样的过程不应该向对方透露他们的数据库知识。

3.8.Sorting Problem:

排序问题： 让Alice和Bob拥有他们的私人数据库，他们共同希望在不泄露彼此数据库的情况下对他们的数据库进行排序。

3.9. Shortest Path Problem:

最短路径问题：让Alice和Bob都有他们的位置数据库，他们想在两个位置A和B中找到最短的路径。

3.10.Privacy Preserving Polynomial Interpolation:

隐私保护多项式插值：让Alice和Bob都有他们的数据库，他们想对一个多项式进行插值。

---

3. SMC problems Proposed by Us

• 让来自不同国家的n所研究型大学在不损害每个数据库安全的前提下，从他们的研究数据库中发现一些当前的研究趋势。
• 让我们考虑一些普通商店的几个店主希望在不透露关于他们数据库的信息的情况下发现顾客的购物趋势/购买模式。
• 让我们考虑一个考虑指纹/拇指印象数据库的情报部门。 现在，如果某个警察局的雇员希望检查某个特定的指纹，它必须无法获得它的完整访问权限，相反，他应该只获得测试结果。
• 或者，如果警察希望根据某人的拇指印象/签名检查他的身份，他们可以查阅银行数据库。 银行数据库只显示拇指印象/签名的匹配结果。
• 让我们考虑位于不同国家的N家医院，它们的医疗数据库和病人的病史存储在一些远程数据库站点上。 如果保险公司希望核实某个人的医疗索赔，他可以从医院的数据库中获得该患者的信息，但医院的数据库并不完全提供，而是只允许访问所请求的信息。
• 让全球所有的大学共同希望相互评估，然后根据他们5年的学习成绩宣布世界前20名大学。 他们都希望保护各自数据库的隐私。
• 让来自几个国家的所有医生团队想共同找到一种治疗特定疾病的药物。 所有人都进行调查研究，只在彼此面前揭示结论，而不揭示整个任务。
• 让我们考虑航空公司，有一个预订数据库为每个国家。 如果一个人想从A国家的A城市预订到B国家的B城市，那么我们需要查阅每个中间国家的数据库。 这些数据库只提供查询的详细信息，而不披露其整个预订数据库。
• 让一个社会组织向位于不同国家的大量慈善信托机构提供资金。 这些慈善信托可以查询该组织以检查请求的资金是否已经发出，但看不到该组织的整个数据库。
• 一些网站提供知识海洋，并包含认证信息。 每当我们进行电子购物/电子商务时，认证数据库首先确认我们是一个经过认证的用户，然后当涉及到付款时，我们的帐号/信用卡号在银行数据库中检查是否正确，如果交易成功完成，则只表示购买了商品。 在这种情况下，认证只检查个人的身份，银行数据库只检查卡号，其他认证和银行数据库是保密的。

---

4. SMC PROBLEM SOLUTIONS

到目前为止提出的所有SMC协议都使用了图1所示的两种方法[2]中的任何一种：

• Cryptographic Approach:加密方法： 在这种方法中，由TTP以加密的形式接收来自几方的输入。
• Randomization Approach:随机化方法： 在这种方法中，来自几方的输入首先与一个随机数串联/关联，以保持其安全性。
  

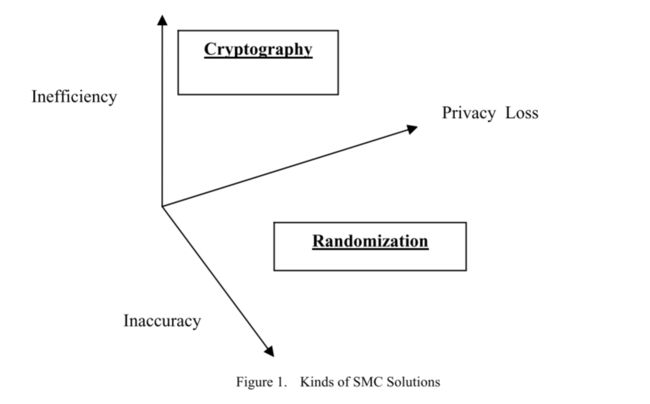
针对SMC问题提出的几种解决方案包括：The Oblivious Protocol, 1-Out Of N Oblivious Protocol, Zero Knowledge Proof, Oblivious Evaluation Of Polynomials, Secret Matching, Threshold Cryptography, Yao’ Millionaire Protocol etc… [1, 4, 5].不经意协议、n中1不经意协议、零知识证明、不经意多项式求值、秘密匹配、门限密码学、Yao’s Millionaire协议等。 [1,4,5]。

在上述方法的基础上，还可以使用安全和、安全集并、集交的安全大小、标量积、EM聚类等技术来寻找SMC解[6]。 另一种机制是在组织和TTP之间引入一个额外的层，称为匿名层[1]。 该匿名层可以对应于每个组织，或者可以跨越多个组织，如图3所示。

---

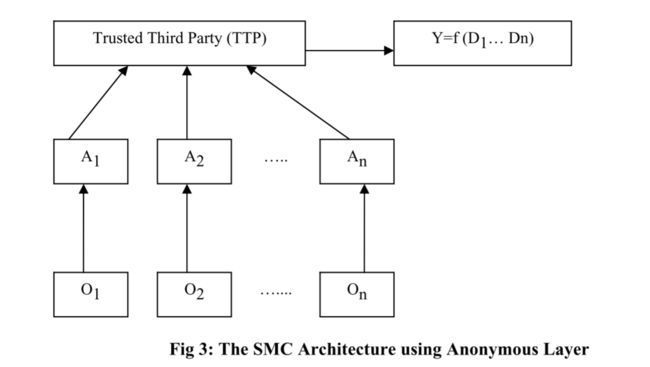
6. CONCLUSION AND FUTURE WORKS:

本文从数据库查询、入侵检测、几何计算、统计分析和科学计算等方面提出了SMC的几个问题及其解决方法。 对于SMC问题的有效解决方案的研究仍在进行中，随着SMC的范围越来越广，这一领域越来越受到人们的关注和重视。 随着计算机的广泛使用，敏感和隐私数据的激增变得非常重要。 本文的主要目的是转移人们的注意力，甚至在其他计算领域的工作，将计算问题视为SMC问题，并提出解决方案。