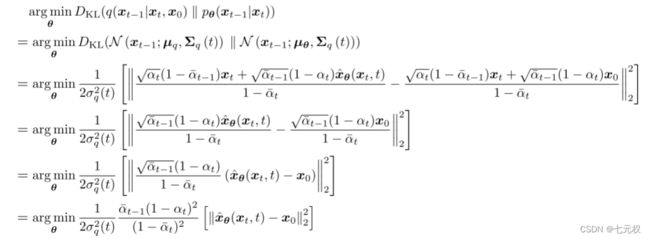论文阅读 - Understanding Diffusion Models: A Unified Perspective
文章目录
- 1 概述
- 2 背景知识
-
- 2.1 直观的例子
- 2.2 Evidence Lower Bound(ELBO)
- 2.3 Variational Autoencoders(VAE)
- 2.4 Hierachical Variational Autoencoders(HVAE)
- 3 Variational Diffusion Models(VDM)
- 4 三个等价的解释
-
- 4.1 预测图片
- 4.2 预测噪声
- 4.3 预测分数
- 5 Guidance
-
- 5.1 Classifier Guidance
- 5.2 Classifier-free Guidance
- 参考资料
1 概述
假设给定了一个数据集 { x 1 , x 2 , x 3 , . . . , x N } \{x_1, x_2, x_3, ..., x_N\} {x1,x2,x3,...,xN},在图像生成任务中,每个 x i x_i xi就是一张图片,每个点都是独立采样于真实数据分布 p ( x ) p(x) p(x)的。生成模型的目的就是通过有限的数据集 { x i } \{x_i\} {xi}学习得到 p ( x ) p(x) p(x),然后从 p ( x ) p(x) p(x)中采样得到更多新的样本。在某些情况下,甚至可以使用 p ( x ) p(x) p(x)来估计某个数据出现的概率。
作者认为,生成模型可以分为三大类:
(1)GAN:通过对抗的方式进行学习,本文不会讲这块
(2)likelihood-based:学习一个使得当前数据集出现概率最高的模型,包括autoregressive models,normalizing flows和VAEs等等
(3)energy-based:将分布学习为任意灵活的能量函数,然后归一化。score-based和energy-based很相似,学的是energy-based model的score。
在某些地方,会讲(2)和(3)都统称为likelihood-based models,而将(1)称为implicit generative models。
而本文重点要讲的Diffusion Model(DM),既可以用likelihood-based的观点来解释,也可以使用score-based的观点来解释。
2 背景知识
2.1 直观的例子
作者在这里引用了柏拉图的地穴寓言来辅助读者理解DM的直观思想,即我们观测到的数据 x x x是由隐变量 z z z生成的,根据观测到的 x x x来估计出隐变量 z z z,就可以通过构造隐变量 z z z来生成 x x x。
如图2-1所示,地穴寓言讲的是一群人一生都被锁在洞穴里,只能看到投射到他们面前墙壁上的二维阴影,这些阴影是由看不见的三维物体在大火前经过而产生的。对这样的人来说,他们所观察到的一切实际上都是由他们永远看不到的高维抽象概念所决定的。

类似的,其实我们现实生活中看到的三维物体,也可能是其他维度的物体投影产生的。
我们的生成模型,就是想从观测到的 x x x中,抽象出隐变量 z z z,这里 z z z的维度通常是低于 x x x的,这是为了抽象出对生成图片真正有用的信息,比如颜色,尺寸,形状等等。
2.2 Evidence Lower Bound(ELBO)
接下来从数学的角度进行说明,我们将隐变量 z z z和观测数据 x x x的联合分布写作 p ( x , z ) p(x,z) p(x,z),根据"likelihood-based"的观点,我们的目的是最大化 p ( x ) p(x) p(x)。 p ( x ) p(x) p(x)和 p ( x , z ) p(x,z) p(x,z)之间的关系,有两种写法:
(1)积分角度
p ( x ) = ∫ p ( x , z ) d z (2-1) p(x) = \int p(x,z) dz \tag{2-1} p(x)=∫p(x,z)dz(2-1)
(2)条件概率角度
p ( x ) = p ( x , z ) p ( z ∣ x ) (2-2) p(x) = \frac{p(x,z)}{p(z|x)} \tag{2-2} p(x)=p(z∣x)p(x,z)(2-2)
根据式 ( 2 − 1 ) (2-1) (2−1)直接算的话,没打算,因为 z z z这个隐变量是未知的,如何积分也就未知了;根据式 ( 2 − 2 ) (2-2) (2−2)算也不行,因为 p ( z ∣ x ) p(z|x) p(z∣x)也是未知的。那么我们为了最大化 p ( x ) p(x) p(x),就需要给它找一个代理目标。
我们设计一个模型,叫做 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x),这个也就是后面会说到的encoder,即根据观测值 x x x预测隐变量 z z z。这个 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x)就是通过优化参数 ϕ \phi ϕ来逼近真实分布 p ( z ∣ x ) p(z|x) p(z∣x)的。由于 1 = ∫ q ϕ ( z ∣ x ) d z 1 = \int q_\phi (z|x) dz 1=∫qϕ(z∣x)dz,所以有
l o g p ( x ) = l o g p ( x ) ∫ q ϕ ( z ∣ x ) d z = ∫ q ϕ ( z ∣ x ) ( l o g p ( x ) ) d z ( 与 z 无关的常量拿进来 ) = E q ϕ ( z ∣ x ) [ l o g p ( x ) ] ( 期望的定义 ) = E q ϕ ( z ∣ x ) [ l o g p ( x , z ) p ( z ∣ x ) ] ( 式 2 − 2 ) = E q ϕ ( z ∣ x ) [ l o g p ( x , z ) q ϕ ( z ∣ x ) p ( z ∣ x ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ l o g p ( x , z ) q ϕ ( z ∣ x ) ] + E q ϕ ( z ∣ x ) [ l o g q ϕ ( z ∣ x ) p ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ l o g p ( x , z ) q ϕ ( z ∣ x ) ] + D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ∣ x ) ) ( K L 散度的定义 ) ≥ E q ϕ ( z ∣ x ) [ l o g p ( x , z ) q ϕ ( z ∣ x ) ] ( K L 散度必然不小于 0 ) (2-3) \begin{align} logp(x) &= logp(x)\int q_\phi (z|x)dz \\ &= \int q_\phi (z|x)(logp(x))dz &\qquad (与z无关的常量拿进来) \\ &= E_{q_\phi (z|x)}[logp(x)] &\qquad (期望的定义)\\ &= E_{q_\phi (z|x)}[log \frac{p(x,z)}{p(z|x)}] &\qquad (式2-2) \\ &= E_{q_\phi (z|x)}[log \frac{p(x,z)q_\phi (z|x)}{p(z|x)q_\phi (z|x)}] &\qquad \\ &= E_{q_\phi (z|x)}[log \frac{p(x,z)}{q_\phi (z|x)}] + E_{q_\phi (z|x)}[log \frac{q_\phi (z|x)}{p(z|x)}]&\qquad \\ &= E_{q_\phi (z|x)}[log \frac{p(x,z)}{q_\phi (z|x)}] + D_{KL}(q_\phi(z|x) || p(z|x))&\qquad (KL散度的定义)\\ &\geq E_{q_\phi (z|x)}[log \frac{p(x,z)}{q_\phi (z|x)}] &\qquad (KL散度必然不小于0) \end{align} \tag{2-3} logp(x)=logp(x)∫qϕ(z∣x)dz=∫qϕ(z∣x)(logp(x))dz=Eqϕ(z∣x)[logp(x)]=Eqϕ(z∣x)[logp(z∣x)p(x,z)]=Eqϕ(z∣x)[logp(z∣x)qϕ(z∣x)p(x,z)qϕ(z∣x)]=Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)]+Eqϕ(z∣x)[logp(z∣x)qϕ(z∣x)]=Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)]+DKL(qϕ(z∣x)∣∣p(z∣x))≥Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)](与z无关的常量拿进来)(期望的定义)(式2−2)(KL散度的定义)(KL散度必然不小于0)(2-3)
这里 E q ϕ ( z ∣ x ) E_{q_\phi (z|x)} Eqϕ(z∣x)表示的是给定 x x x,根据 z ∼ q ϕ ( z ∣ x ) z \sim q_\phi (z|x) z∼qϕ(z∣x)采样得到的所有 z z z下的期望。还想不明白,可以从离散的角度思考一下,遍历所有的 z z z去算期望,只不过每个 z z z有对应的概率 q ϕ ( z ∣ x ) q_\phi (z|x) qϕ(z∣x)。
推导到这里, l o g p ( x ) logp(x) logp(x)的下界就出现了,为了突出其重要性,这里单独再写一下
E q ϕ ( z ∣ x ) [ l o g p ( x , z ) q ϕ ( z ∣ x ) ] (2-4) E_{q_\phi (z|x)}[log \frac{p(x,z)}{q_\phi (z|x)}] \tag{2-4} Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)](2-4)
式 ( 2 − 4 ) (2-4) (2−4)就是ELBO,其中evidence就是指的 l o g p ( x ) logp(x) logp(x),其lower bound就是式 ( 2 − 4 ) (2-4) (2−4)。
我们来分析一下式 ( 2 − 3 ) (2-3) (2−3),它与 l o g p ( x ) logp(x) logp(x)之间只相差了一个KL散度 D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ∣ x ) ) D_{KL}(q_\phi(z|x) || p(z|x)) DKL(qϕ(z∣x)∣∣p(z∣x)), D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ∣ x ) ) D_{KL}(q_\phi(z|x) || p(z|x)) DKL(qϕ(z∣x)∣∣p(z∣x))表示了模型学习的分布 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x)与真实分布 p ( z ∣ x ) p(z|x) p(z∣x)之间的距离。由于 x x x是我们的数据集,是固定不变的,因此 l o g p ( x ) logp(x) logp(x)就是一个常数,因此式 ( 2 − 4 ) (2-4) (2−4)越大, D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ∣ x ) ) D_{KL}(q_\phi(z|x) || p(z|x)) DKL(qϕ(z∣x)∣∣p(z∣x))就越小, q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x)与 p ( z ∣ x ) p(z|x) p(z∣x)就越接近。总而言之,就是可以通过最大化式 ( 2 − 4 ) (2-4) (2−4)来最小化KL散度 D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ∣ x ) ) D_{KL}(q_\phi(z|x) || p(z|x)) DKL(qϕ(z∣x)∣∣p(z∣x))。 D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ∣ x ) ) D_{KL}(q_\phi(z|x) || p(z|x)) DKL(qϕ(z∣x)∣∣p(z∣x))没法直接最小化,因为 p ( z ∣ x ) p(z|x) p(z∣x)是不知道的。
除此之外,训练好之后,式 ( 2 − 4 ) (2-4) (2−4)会和 l o g p ( x ) logp(x) logp(x)很接近,因此可以当做 l o g p ( x ) logp(x) logp(x)来估计观测数据或者生成数据的出现概率。
2.3 Variational Autoencoders(VAE)
在介绍VAE之前,读者最好对VAE有个初步的认识,可以参考我的另一篇博客论文阅读 - Jukebox: A Generative Model for Music。
我们令 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x)为VAE中的encoder, p θ ( x ∣ z ) p_\theta(x|z) pθ(x∣z)为VAE中的decoder,对式 ( 2 − 4 ) (2-4) (2−4)进行变形,则有
E q ϕ ( z ∣ x ) [ l o g p ( x , z ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ l o g p θ ( x ∣ z ) p ( z ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ l o g p θ ( x ∣ z ) ] + E q ϕ ( z ∣ x ) [ l o g p ( z ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ l o g p θ ( x ∣ z ) ] − D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ) (2-5) \begin{align} E_{q_\phi (z|x)}[log \frac{p(x,z)}{q_\phi (z|x)}] &= E_{q_\phi (z|x)}[log \frac{p_\theta(x|z)p(z)}{q_\phi (z|x)}] \\ &= E_{q_\phi (z|x)}[log p_\theta(x|z)] + E_{q_\phi (z|x)}[log \frac{p(z)}{q_\phi (z|x)}] \\ &= E_{q_\phi (z|x)}[log p_\theta(x|z)] - D_{KL}(q_\phi (z|x) || p(z)) \end{align} \tag{2-5} Eqϕ(z∣x)[logqϕ(z∣x)p(x,z)]=Eqϕ(z∣x)[logqϕ(z∣x)pθ(x∣z)p(z)]=Eqϕ(z∣x)[logpθ(x∣z)]+Eqϕ(z∣x)[logqϕ(z∣x)p(z)]=Eqϕ(z∣x)[logpθ(x∣z)]−DKL(qϕ(z∣x)∣∣p(z))(2-5)
这里的第一个等号,我认为并不能直接等过来,因为 p θ ( x ∣ z ) p_\theta(x|z) pθ(x∣z)只是 p ( x ∣ z ) p(x|z) p(x∣z)的一个估计,而且取决于模型的训练效果,这里存疑,之后想明白了这里会改过来。
我们假设已经等过来了,那么式 ( 2 − 5 ) (2-5) (2−5)的前一项 E q ϕ ( z ∣ x ) [ l o g p θ ( x ∣ z ) ] E_{q_\phi (z|x)}[log p_\theta(x|z)] Eqϕ(z∣x)[logpθ(x∣z)]表示的是decoder重建图片的似然度,称作reconstruction term;后一项 D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ) D_{KL}(q_\phi (z|x) || p(z)) DKL(qϕ(z∣x)∣∣p(z))表示经过encoder得到的 z z z的分布与先验 p ( z ) p(z) p(z)之间的距离,称作prior matching term。
将ELBO最大化,就相当于最大化reconstruction term,同时最小化prior matching term。
VAE的encoder通常被设计为对角方差的多元高斯,所谓对角方差,就是没有协方差的意思,如下式 ( 2 − 6 ) (2-6) (2−6)所示。
q ϕ ( z ∣ x ) = N ( z ; μ ϕ ( x ) , σ ϕ 2 ( x ) I ) (2-6) q_\phi (z|x) = N(z;\mu_\phi(x), \sigma_\phi ^2(x)I) \tag{2-6} qϕ(z∣x)=N(z;μϕ(x),σϕ2(x)I)(2-6)
与其对应的prior为标准的多元高斯,如下式 ( 2 − 6 ) (2-6) (2−6)所示。
p ( z ) = N ( z ; 0 , I ) (2-7) p(z) = N(z;0, I) \tag{2-7} p(z)=N(z;0,I)(2-7)
结合式 ( 2 − 6 ) (2-6) (2−6)和式 ( 2 − 6 ) (2-6) (2−6),式 ( 2 − 5 ) (2-5) (2−5)的后一项,也就是KL散度这项是可以算出解析解的,而式 ( 2 − 5 ) (2-5) (2−5)的前一项则通过蒙特卡洛估计得到,也就是连续离散,使用有限的数据集来估计期望 E q ϕ ( z ∣ x ) [ l o g p θ ( x ∣ z ) ] E_{q_\phi (z|x)}[log p_\theta(x|z)] Eqϕ(z∣x)[logpθ(x∣z)]。
于是,我们的目标函数可以写成
a r g max ϕ , θ E q ϕ ( z ∣ x ) [ l o g p θ ( x ∣ z ) ] − D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ) = a r g max ϕ , θ ∑ l = 1 L l o g p θ ( x ∣ z ( l ) ) − D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ) (2-8) arg\max_{\phi,\theta}E_{q_\phi(z|x)}[logp_\theta(x|z)] - D_{KL}(q_\phi (z|x) || p(z)) = \\ arg\max_{\phi,\theta}\sum_{l=1}^Llogp_\theta(x|z^{(l)}) - D_{KL}(q_\phi (z|x) || p(z)) \tag{2-8} argϕ,θmaxEqϕ(z∣x)[logpθ(x∣z)]−DKL(qϕ(z∣x)∣∣p(z))=argϕ,θmaxl=1∑Llogpθ(x∣z(l))−DKL(qϕ(z∣x)∣∣p(z))(2-8)
其中, z ( l ) l = 1 L {z^{(l)}}_{l=1}^L z(l)l=1L是从 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x)中采样得到的,也就是数据集的图片过一遍encoder。不过这里有一个问题,就是每个 z ( l ) z^{(l)} z(l)都是通过随机高斯分布采样的过程得到的,没有办法求导。为了解决这个问题,就有了重参化技巧,重参化的精妙之处在于使用标准的随机过程构造任意随机过程,学习只学习构造的参数,而随机过程是不参与梯度计算的。
举个例子,假设随机过程为 x ∼ N ( x ; μ , σ 2 ) x \sim N(x;\mu, \sigma^2) x∼N(x;μ,σ2),这可以写作
x = μ + σ ϵ , ϵ ∼ N ( 0 , I ) x = \mu + \sigma \epsilon, \epsilon \sim N(0, I) x=μ+σϵ,ϵ∼N(0,I)
在VAE当中,任意一次从 q ϕ ( z ∣ x ) q_\phi (z|x) qϕ(z∣x)中对 z z z的采样可以表示为
z = μ ϕ ( x ) + σ ϕ ( x ) ⊙ ϵ , ϵ ∼ N ( 0 , I ) z = \mu_\phi(x) + \sigma_\phi(x) \odot\epsilon, \epsilon \sim N(0, I) z=μϕ(x)+σϕ(x)⊙ϵ,ϵ∼N(0,I)
其中, ⊙ \odot ⊙表示element-wise的乘积。
VAE就是借助与重参化的技巧和蒙特卡洛估计来同时更新 ϕ \phi ϕ和 θ \theta θ的。
训练完成后,只需要在 p ( z ) = N ( z ; 0 , I ) p(z) = N(z;0, I) p(z)=N(z;0,I)上进行采样,输入decoder就可以得到预测的结果了,encoder已经不需要了。
z z z的维度通常大大小于 x x x,这样可以迫使模型学习最有用的特征表示。
2.4 Hierachical Variational Autoencoders(HVAE)
HVAE就是在VAE的基础上再增加了多层的隐变量,也就是隐变量也是通过更深一层的隐变量生成的。一般情况下,HVAE中的每一层隐变量 z t z_t zt是由其之前的所有隐变量决定的,不过本文只针对马尔可夫过程的HVAE,也就是 z t z_t zt仅由 z t + 1 z_{t+1} zt+1决定,这也被称为MHVAE,如下图2-3所示。

此时, x x x和 z t z_t zt的联合概率可以写作(也就是图2-3上方乘起来)
p ( x , z 1 : T ) = p ( z T ) p θ ( x ∣ z 1 ) ∏ t = 2 T p θ ( z t − 1 ∣ z t ) (2-9) p(x, z_{1:T}) = p(z_T)p_\theta(x|z_1)\prod_{t=2}^Tp_\theta(z_{t-1}|z_t) \tag{2-9} p(x,z1:T)=p(zT)pθ(x∣z1)t=2∏Tpθ(zt−1∣zt)(2-9)
后验概率可以写作(也就是图2-3下方乘起来)
q ϕ ( z 1 : T ∣ x ) = q ϕ ( z 1 ∣ x ) ∏ t = 2 T q ϕ ( z t ∣ z t − 1 ) (2-10) q_\phi (z_{1:T}|x) = q_\phi(z_1|x)\prod_{t=2}^Tq_\phi(z_t|z_{t-1}) \tag{2-10} qϕ(z1:T∣x)=qϕ(z1∣x)t=2∏Tqϕ(zt∣zt−1)(2-10)
此时的ELBO可以被改写为

(2-11) \ \tag{2-11} (2-11)
其中,最后一步用到了琴生不等式,这也是式 ( 2 − 3 ) (2-3) (2−3)的另一种推导方式。
将式 ( 2 − 9 ) (2-9) (2−9)和式 ( 2 − 10 ) (2-10) (2−10)代入式 ( 2 − 11 ) (2-11) (2−11)可以得到
E q ϕ ( z 1 : T ∣ x ) [ l o g p ( x , z 1 : T ) q ϕ ( z 1 : T ∣ x ) ] = E q ϕ ( z 1 : T ∣ x ) [ l o g p ( z T ) p θ ( x ∣ z 1 ) ∏ t = 2 T p θ ( z t − 1 ∣ z t ) q ϕ ( z 1 ∣ x ) ∏ t = 2 T q ϕ ( z t ∣ z t − 1 ) ] (2-12) E_{q_\phi (z_{1:T}|x)}[log \frac{p(x,z_{1:T})}{q_\phi (z_{1:T}|x)}] = E_{q_\phi (z_{1:T}|x)}[log\frac{p(z_T)p_\theta(x|z_1)\prod_{t=2}^Tp_\theta(z_{t-1}|z_t)}{q_\phi(z_1|x)\prod_{t=2}^Tq_\phi(z_t|z_{t-1})}] \tag{2-12} Eqϕ(z1:T∣x)[logqϕ(z1:T∣x)p(x,z1:T)]=Eqϕ(z1:T∣x)[logqϕ(z1∣x)∏t=2Tqϕ(zt∣zt−1)p(zT)pθ(x∣z1)∏t=2Tpθ(zt−1∣zt)](2-12)
式 ( 2 − 12 ) (2-12) (2−12)将在下文的VDM中被拆解为可解释的多个部分。
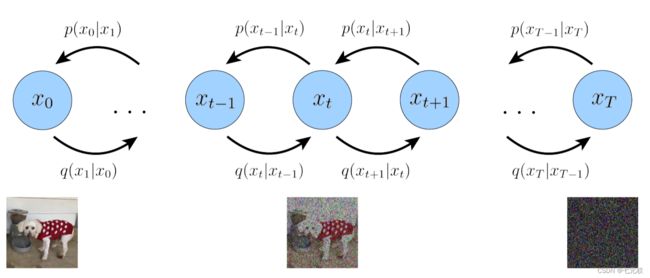
3 Variational Diffusion Models(VDM)
一种理解VDM最简单的思路,就是将VDM看成MHVAE,如图3-1所示,不过需要满足三个额外的限制:
(1)隐变量的维度需要和输入图片维度一致
(2)encoder的每一步不是学习得到的,是事先设计好的线性高斯分布。换句话说,每一步是以上一步为中心的高斯分布
(3)每一步的高斯分布参数会发生一定的变化,使得最后一步接近标准高斯分布
根据第一点限制,我们不用分 z z z和 x x x了,统一使用 x t x_t xt来表示任意时刻的数据即可。当 t = 0 t=0 t=0时, x 0 x_0 x0指的是原始图片。当 t ∈ [ 1 , T ] t\in [1,T] t∈[1,T]时,表示对应步数的数据。如此以来,后验概率式 ( 2 − 10 ) (2-10) (2−10)可以写成
q ϕ ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ϕ ( x t ∣ x t − 1 ) (3-1) q_\phi (x_{1:T}|x_0) = \prod_{t=1}^Tq_\phi(x_t|x_{t-1}) \tag{3-1} qϕ(x1:T∣x0)=t=1∏Tqϕ(xt∣xt−1)(3-1)
根据第二点限制,每一步的高斯参数人为设计为 μ t ( x t ) = α t x t − 1 \mu_t(x_t) = \sqrt{\alpha_t}x_{t-1} μt(xt)=αtxt−1, Σ t ( x t ) = ( 1 − α t ) I \Sigma_t(x_t) = (1-\alpha_t)I Σt(xt)=(1−αt)I,其中 α t \alpha_t αt是一个潜在的可学习的参数,这里是个超参数,随着步数的变化而变化。因此,有
q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) (3-2) q(x_t|x_{t-1}) = N(x_t;\sqrt{\alpha_t}x_{t-1}, (1-\alpha_t)I) \tag{3-2} q(xt∣xt−1)=N(xt;αtxt−1,(1−αt)I)(3-2)
根据第三点限制,最终的分布 p ( x T ) p(x_T) p(xT)是一个标准的高斯分布,其本质是真实分布逐渐变为标准高斯分布的过程。因此,式 ( 2 − 9 ) (2-9) (2−9)可以写作
p ( x 0 : T ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) (3-3) p(x_{0:T}) = p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t) \tag{3-3} p(x0:T)=p(xT)t=1∏Tpθ(xt−1∣xt)(3-3)
其中, p ( x T ) = N ( x T ; 0 , I ) p(x_T)=N(x_T;0, I) p(xT)=N(xT;0,I)。
在VDM中, q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)是人为事先设计的,已经与参数 ϕ \phi ϕ没有关系了,所以我们需要学习的参数只有 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)中的 θ \theta θ而已。当VDM整个模型训练好之后,只需要在标准高斯分布 p ( x T ) = N ( x T ; 0 , I ) p(x_T)=N(x_T;0, I) p(xT)=N(xT;0,I)中采样,再一步步经过 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)生成图片即可。
VDM的优化也是通过最大化ELBO的,推导过程为
最终得到的结果可以被解释为reconstruntion term,prior matching term和consistency term三项。
reconstruction term和VAE中的很像,就是最终生成图片的似然概率,训练方式也和VAE中的类似。也就是要是的生成的图片和真实图片越接近越好。
proir matching term这一项没有训练参数,当 T T T足够大时, q ( x T ∣ x T − 1 ) q(x_T|x_{T-1}) q(xT∣xT−1)会趋近于 N ( x T ; 0 , I ) N(x_T;0, I) N(xT;0,I),因此这项可以认为是0。
consistency term是为了保证正向的过程和逆向的过程是一致的,也就是加噪声和去噪声是需要一致的。这也是训练的主导项。
在这种推导方式下,ELBO的所有项都是期望,因此可以通过蒙特卡洛方法来进行估计。但是,实际使用式 ( 3 − 4 ) (3-4) (3−4)进行估计的方案是次优的,因为consistency term的每一步都有两个随机变量 { x t − 1 , x t + 1 } \{x_{t-1}, x_{t+1}\} {xt−1,xt+1},这种情况下的蒙特卡洛估计方差会大于只有一个随机变量的方式。这是为啥,我也不太清楚,姑且就假设这是一个正确的结论吧。
因此,为了将期望当中的随机变量变为一个,我们要进行一些改动。由于整个过程是满足马尔可夫链的,因此 x t x_t xt只由 x t − 1 x_{t-1} xt−1决定,于是就有 q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) q(x_t|x_{t-1}) = q(x_t|x_{t-1}, x_0) q(xt∣xt−1)=q(xt∣xt−1,x0)。根据贝叶斯定理,每一次的正向加噪过程可以写作
q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) (3-5) q(x_t|x_{t-1}, x_0) = \frac{q(x_{t-1}|x_t, x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)} \tag{3-5} q(xt∣xt−1,x0)=q(xt−1∣x0)q(xt−1∣xt,x0)q(xt∣x0)(3-5)
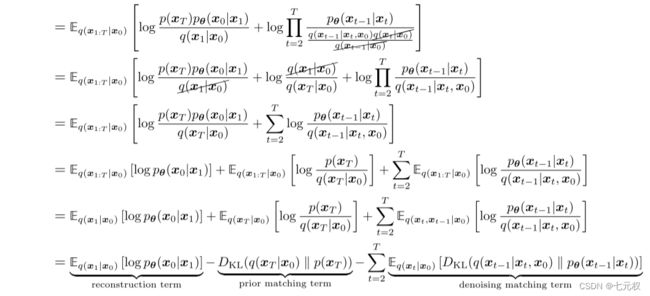
基于式 ( 3 − 5 ) (3-5) (3−5),可以重新推导ELBO
推导的结果又可以被解释为三项,分别是reconstruntion term,prior matching term和denoising matching term。
reconstruntion term没有发生变化,仍旧是生成图片的似然度,可以和VAE一样使用蒙特卡洛估计来进行优化
prior matching term没有可训练的参数,表示最终加满噪声的图片和标准高斯分布的距离,可以认为是0
denoising matching term表示去噪过程是否和加噪过程一致。 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q(xt−1∣xt,x0)可以认为是GT,也就是真实的去噪过程。 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)要尽可能和 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q(xt−1∣xt,x0)一致。
值得一提的是,式 ( 3 − 5 ) (3-5) (3−5)和式 ( 3 − 6 ) (3-6) (3−6)的整个推导过程,只用到了马尔可夫假设,因此适用于任意的MHVAE。当 T = 1 T=1 T=1时,式 ( 3 − 5 ) (3-5) (3−5)和式 ( 3 − 6 ) (3-6) (3−6)都变成了式 ( 2 − 5 ) (2-5) (2−5)。
式 ( 3 − 6 ) (3-6) (3−6)中的主导项还是最后一项denoising matching term。根据贝叶斯定理,我们有
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) (3-7) q(x_{t-1}|x_t, x_0) = \frac{q(x_t|x_{t-1}, x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)} \tag{3-7} q(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1,x0)q(xt−1∣x0)(3-7)
其中,根据式 ( 3 − 2 ) (3-2) (3−2)有 q ( x t ∣ x t − 1 , x 0 ) = q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) q(x_t|x_{t-1}, x_0) = q(x_t|x_{t-1}) = N(x_t;\sqrt{\alpha_t}x_{t-1}, (1-\alpha_t)I) q(xt∣xt−1,x0)=q(xt∣xt−1)=N(xt;αtxt−1,(1−αt)I),目前需要确定的就是 q ( x t − 1 ∣ x 0 ) q(x_{t-1}|x_0) q(xt−1∣x0)和 q ( x t ∣ x 0 ) q(x_t|x_0) q(xt∣x0)。根据重参化技巧,对于 x t ∼ q ( x t ∣ x t − 1 ) x_t \sim q(x_t|x_{t-1}) xt∼q(xt∣xt−1)可以写作
x t = α t x t − 1 + 1 − α t ϵ (3-8) x_t = \sqrt{\alpha_t}x_{t-1} + \sqrt{1-\alpha_t}\epsilon \tag{3-8} xt=αtxt−1+1−αtϵ(3-8)
同理,有
x t − 1 = α t − 1 x t − 2 + 1 − α t − 1 ϵ (3-9) x_{t-1} = \sqrt{\alpha_{t-1}}x_{t-2} + \sqrt{1-\alpha_{t-1}}\epsilon \tag{3-9} xt−1=αt−1xt−2+1−αt−1ϵ(3-9)
不断地迭代,代入,可以得到
x t = ∏ i = 1 t α i x 0 + 1 − ∏ i = 1 t α i ϵ = α ‾ t x 0 + 1 − α ‾ t ϵ ∼ N ( x t ; α ‾ t x 0 , 1 − α ‾ t I ) (3-10) \begin{align} x_t &= \sqrt{\prod_{i=1}^t \alpha_i}x_{0} + \sqrt{1 - \prod_{i=1}^t \alpha_i}\epsilon \\ &= \sqrt{\overline{\alpha}_t}x_0 + \sqrt{1-\overline{\alpha}_t}\epsilon \\ &\sim N(x_t; \sqrt{\overline{\alpha}_t}x_0, 1-\overline{\alpha}_t I) \end{align} \tag{3-10} xt=i=1∏tαix0+1−i=1∏tαiϵ=αtx0+1−αtϵ∼N(xt;αtx0,1−αtI)(3-10)
这里省略了推导过程,想了解的可以参见原文。
式 ( 3 − 10 ) (3-10) (3−10)就是 q ( x t ∣ x 0 ) q(x_t|x_0) q(xt∣x0),其重大意义在于,任意的 x t x_t xt不用一步步加噪声,而是可以直接通过 x 0 x_0 x0得到了。 q ( x t − 1 ∣ x 0 ) q(x_{t-1}|x_0) q(xt−1∣x0)同理也可以得到,这里就不赘述了。
回到式 ( 3 − 7 ) (3-7) (3−7),我们有
回到式 ( 3 − 6 ) (3-6) (3−6)的denoising matching term,这里注意到 Σ q ( t ) = σ q 2 ( t ) I \Sigma_q(t)=\sigma_q^2(t)I Σq(t)=σq2(t)I是一个常数,所以我们也可以将 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)的方差设置为同样的常数。
两个高斯分布之间的KL散度的计算公式为
D K L ( N ( x ; μ x , Σ x ) ∣ ∣ N ( y ; μ y , Σ y ) ) = 1 2 [ l o g ∣ Σ y ∣ ∣ Σ x ∣ − d + t r ( Σ y − 1 Σ x ) + ( μ y − μ x ) T Σ y − 1 ( μ y − μ x ) ] (3-12) D_{KL}(N(x;\mu_x, \Sigma_x)||N(y;\mu_y, \Sigma_y)) = \frac{1}{2}[log\frac{|\Sigma_y|}{|\Sigma_x|} -d + tr(\Sigma_y^{-1}\Sigma_x) +(\mu_y-\mu_x)^T\Sigma_y^{-1}(\mu_y - \mu_x)] \tag{3-12} DKL(N(x;μx,Σx)∣∣N(y;μy,Σy))=21[log∣Σx∣∣Σy∣−d+tr(Σy−1Σx)+(μy−μx)TΣy−1(μy−μx)](3-12)
于是就有

其中, μ θ \mu_\theta μθ和 μ q \mu_q μq是 μ θ ( x t , t ) \mu_\theta(x_t, t) μθ(xt,t)和 μ q ( x t , x 0 ) \mu_q(x_t, x_0) μq(xt,x0)的简写。
根据式 ( 3 − 11 ) (3-11) (3−11)有
μ q ( x t , x 0 ) = α t ( 1 − α ‾ t − 1 ) x t + α ‾ t − 1 ( 1 − α t ) x 0 1 − α ‾ t (3-13) \mu_q(x_t, x_0) = \frac{\sqrt{\alpha_t}(1-\overline{\alpha}_{t-1})x_t+\sqrt{\overline{\alpha}_{t-1}}(1-\alpha_t)x_0}{1-\overline{\alpha}_t} \tag{3-13} μq(xt,x0)=1−αtαt(1−αt−1)xt+αt−1(1−αt)x0(3-13)
我们可以将 μ θ ( x t , t ) \mu_\theta(x_t, t) μθ(xt,t)设计为
μ θ ( x t , t ) = α t ( 1 − α ‾ t − 1 ) x t + α ‾ t − 1 ( 1 − α t ) x ^ θ ( x t , t ) 1 − α ‾ t (3-14) \mu_\theta(x_t, t) = \frac{\sqrt{\alpha_t}(1-\overline{\alpha}_{t-1})x_t+\sqrt{\overline{\alpha}_{t-1}}(1-\alpha_t)\hat{x}_\theta(x_t, t)}{1-\overline{\alpha}_t} \tag{3-14} μθ(xt,t)=1−αtαt(1−αt−1)xt+αt−1(1−αt)x^θ(xt,t)(3-14)
这里的 x ^ θ ( x t , t ) \hat{x}_\theta(x_t, t) x^θ(xt,t)就是我们的设计的神经网络,输入是噪声图片 x t x_t xt和步数索引 t t t,输出是生成的图片。
denoising matching term可以写作
(3-15) \ \tag{3-15} (3-15)
于是,VDM就变成了学习一个神经网络,在任意的加噪步的位置预测出原始图片 x 0 x_0 x0,将所有时间步的期望求和,就有
a r g min θ E t ∼ U { 2 , T } [ E q ( x t ∣ x 0 ) D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) ] (3-16) arg\min_\theta E_{t\sim U\{2, T\}}[E_{q(x_t|x_0)}D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))] \tag{3-16} argθminEt∼U{2,T}[Eq(xt∣x0)DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))](3-16)
4 三个等价的解释
VDM可以设计网络来预测图片,设计网络来预测噪声,也可以设计网络来预测分数,接下来分别讲一下。
4.1 预测图片
预测图片的方式就是式 ( 3 − 15 ) (3-15) (3−15)中描述的方式,即将网络设计为 x ^ θ ( x t , t ) \hat{x}_\theta(x_t, t) x^θ(xt,t)来预测原始图片,这里不在赘述。
4.2 预测噪声
将式 ( 3 − 10 ) (3-10) (3−10)做一个变形可以得到
x 0 = x t − 1 − α ‾ t ϵ α ‾ t (4-1) x_0 = \frac{x_t - \sqrt{1 - \overline{\alpha}_t}\epsilon}{\sqrt{\overline{\alpha}_t}} \tag{4-1} x0=αtxt−1−αtϵ(4-1)
将其代入式 ( 3 − 13 ) (3-13) (3−13)可以得到

(4-2) \ \tag{4-2} (4-2)
于是,我们重新设计 μ θ ( x t , t ) \mu_\theta(x_t, t) μθ(xt,t)为
μ θ ( x t , t ) = 1 α t x t − 1 − α t 1 − α ‾ t α t ϵ ^ θ ( x t , t ) (4-3) \mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}}x_t - \frac{1-\alpha_t}{\sqrt{1-\overline{\alpha}_t}\sqrt{\alpha_t}}\hat{\epsilon}_\theta(x_t, t) \tag{4-3} μθ(xt,t)=αt1xt−1−αtαt1−αtϵ^θ(xt,t)(4-3)
对应的denoising matching term可以写作

(4-4) \ \tag{4-4} (4-4)
其实可以认为是把 x 0 x_0 x0用 ϵ \epsilon ϵ来表示,然后系数什么变了一下。从理论上来说,预测原图 x 0 x_0 x0和预测噪声 ϵ \epsilon ϵ是等价的。
但是从实际经验上来说,预测噪声 ϵ \epsilon ϵ的效果会更好一些。
4.3 预测分数
预测分数的推导需要借助于Tweedie’s formula,从数学的角度来说,对于高斯变量 z ∼ N ( z ; μ z , Σ z ) z \sim N(z;\mu_z, \Sigma_z) z∼N(z;μz,Σz),Tweedie’s formula指出
E [ μ z ∣ z ] = z + Σ z ∇ z l o g p ( z ) (4-5) E[\mu_z|z] = z+\Sigma_z\nabla_zlogp(z) \tag{4-5} E[μz∣z]=z+Σz∇zlogp(z)(4-5)
不知道这个公式怎么来的没关系,这是个结论,我们暂且认为它是对的。
对于式 ( 3 − 10 ) (3-10) (3−10)使用Tweedie’s formula,可以得到
E [ μ x t ∣ x t ] = x t + ( 1 − α ‾ t ) ∇ x t l o g p ( x t ) (4-6) E[\mu_{x_t}|x_t] = x_t + (1 - \overline{\alpha}_t)\nabla_{x_t}logp(x_t) \tag{4-6} E[μxt∣xt]=xt+(1−αt)∇xtlogp(xt)(4-6)
后面为了方便表示,将 ∇ x t l o g p ( x t ) \nabla_{x_t}logp(x_t) ∇xtlogp(xt)简写为 ∇ l o g p ( x t ) \nabla logp(x_t) ∇logp(xt)。根据式 ( 3 − 10 ) (3-10) (3−10),有 μ x t = α ‾ t x 0 \mu_{x_t}=\sqrt{\overline{\alpha}_t}x_0 μxt=αtx0,再结合式 ( 4 − 6 ) (4-6) (4−6)就有
α ‾ t x 0 = x t + ( 1 − α ‾ t ) ∇ x t l o g p ( x t ) x 0 = x t + ( 1 − α ‾ t ) ∇ x t l o g p ( x t ) α ‾ t (4-7) \sqrt{\overline{\alpha}_t}x_0 = x_t + (1 - \overline{\alpha}_t)\nabla_{x_t}logp(x_t) \\ x_0 = \frac{x_t + (1 - \overline{\alpha}_t)\nabla_{x_t}logp(x_t)}{\sqrt{\overline{\alpha}_t}} \tag{4-7} αtx0=xt+(1−αt)∇xtlogp(xt)x0=αtxt+(1−αt)∇xtlogp(xt)(4-7)
然后,和4.2一样的套路,将其代入式 ( 3 − 13 ) (3-13) (3−13),可以有

(4-8) \ \tag{4-8} (4-8)
于是,我们重新设计 μ θ ( x t , t ) \mu_\theta(x_t, t) μθ(xt,t)为
μ θ ( x t , t ) = 1 α t x t + 1 − α t α t s θ ( x t , t ) (4-9) \mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}}x_t + \frac{1 - \alpha_t}{\sqrt{\alpha_t}}s_{\theta}(x_t, t) \tag{4-9} μθ(xt,t)=αt1xt+αt1−αtsθ(xt,t)(4-9)
对应的denoising matching term可以写作
(4-10) \ \tag{4-10} (4-10)
这里的 s θ ( x t , t ) s_\theta(x_t, t) sθ(xt,t)就是一个用来预测score function ∇ x t l o g p ( x t ) \nabla_{x_t}logp(x_t) ∇xtlogp(xt)的神经网络。用心的读者可以发现, ∇ x t l o g p ( x t ) \nabla_{x_t}logp(x_t) ∇xtlogp(xt)和 ϵ \epsilon ϵ很像。我们结合式 ( 4 − 7 ) (4-7) (4−7)和式 ( 4 − 1 ) (4-1) (4−1)可以得到
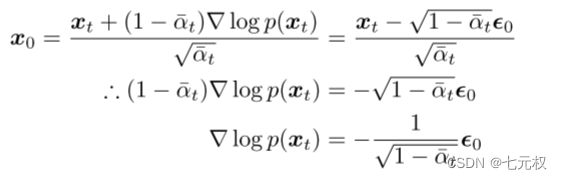
(4-11) \ \tag{4-11} (4-11)
可以看出,就是差了一个缩放系数常数。同时也可以发现,他们的正负号是相反的,也就是说,往加噪的反方向来去噪是最佳更新模型参数的路径。
5 Guidance
到目前为止,我们的重心都放在真实数据的分布 p ( x ) p(x) p(x)上,但我们通常更加关注某些条件下的真实数据分布 p ( x ∣ y ) p(x|y) p(x∣y)。这可以让我们在一定程度上控制生成的图片。
一个很自然的想法就是在每一步都加上条件,于是式 ( 3 − 3 ) (3-3) (3−3)可以改写为
p ( x 0 : T ∣ y ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t , y ) (5-1) p(x_{0:T}|y) = p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t, y) \tag{5-1} p(x0:T∣y)=p(xT)t=1∏Tpθ(xt−1∣xt,y)(5-1)
y y y可以是文本,可以是其他图片,也可以是一个类别。对应到章节4中的三种解释,VDM的目标就变成了 x ^ θ ( x t , t , y ) ≈ x 0 \hat{x}_\theta (x_t, t, y) \approx x_0 x^θ(xt,t,y)≈x0,或者 ϵ ^ θ ( x t , t , y ) ≈ ϵ \hat{\epsilon}_\theta (x_t, t, y) \approx \epsilon ϵ^θ(xt,t,y)≈ϵ,或者 s θ ( x t , t , y ) ≈ ∇ l o g p ( x t ∣ y ) s_\theta(x_t, t, y) \approx \nabla log p(x_t|y) sθ(xt,t,y)≈∇logp(xt∣y)。
目前有两种主流的控制方式,分别是Classifier Guidance和Classifier-free Guidance。
5.1 Classifier Guidance
我们使用基于分数的公式来进行说明,目标就是学习 ∇ l o g p ( x t ∣ y ) \nabla log p(x_t|y) ∇logp(xt∣y)。根据贝叶斯公式,我们有

(5-2) \ \tag{5-2} (5-2)
其中,第二行的 p ( y ) p(y) p(y)关于 x t x_t xt的导数是0,就没有了。
最终,式 ( 5 − 2 ) (5-2) (5−2)可以理解为无条件分数和一个分类器 p ( y ∣ x t ) p(y|x_t) p(y∣xt)的梯度。
为了更加细粒度地控制条件的重要程度,还会加上一个超参数 γ \gamma γ,于是就有
∇ l o g p ( x t ∣ y ) = ∇ l o g p ( x t ) + γ ∇ l o g p ( y ∣ x t ) (5-3) \nabla log p(x_t|y) = \nabla log p(x_t) + \gamma \nabla log p(y|x_t) \tag{5-3} ∇logp(xt∣y)=∇logp(xt)+γ∇logp(y∣xt)(5-3)
当 γ = 0 \gamma = 0 γ=0时,就是无条件的,当 γ \gamma γ很大时,会依赖于条件,往往会损失生成结果的多样性。
Classifier Guidance的缺点就是需要处理任意噪声输入,没有可以直接使用的预训练好的classifier,需要和VDM一起进行训练。
5.2 Classifier-free Guidance
Classifier-free Guidance的方案不需要单独的分类模型。
将式 ( 5 − 2 ) (5-2) (5−2)做一些变形,可以得到
∇ l o g p ( y ∣ x t ) = ∇ l o g p ( x t ∣ y ) − ∇ l o g p ( x t ) (5-4) \nabla log p(y|x_t) = \nabla log p(x_t|y) - \nabla log p(x_t) \tag{5-4} ∇logp(y∣xt)=∇logp(xt∣y)−∇logp(xt)(5-4)
将式 ( 5 − 4 ) (5-4) (5−4)代入式 ( 5 − 3 ) (5-3) (5−3)可以得到

同样, γ \gamma γ是一个控制我们学习的条件模型对条件信息的关注程度的超参数。当 γ = 0 \gamma=0 γ=0时,学习的条件模型完全忽略条件器并学习无条件扩散模型;当 γ = 1 \gamma=1 γ=1时,该模型在没有指导的情况下显式地学习条件分布;当 γ > 1 \gamma>1 γ>1时,扩散模型不仅优先考虑条件得分函数,而且在远离无条件得分函数的方向上移动。换句话说,它降低了生成不使用条件信息的样本的概率,有利于显式地使用条件信息的样本。
由于学习两个独立的扩散模型是昂贵的,我们可以同时学习条件和无条件扩散模型作为一个单一的条件模型。无条件扩散模型可以通过用诸如零的固定常数值替换条件信息来查询,这本质上是对条件信息进行dropout。
Classifier-free Guidance是优雅的,因为它使我们能够更好地控制我们的条件生成过程,同时只需要正常的扩散模型训练。
参考资料
[1] Understanding Diffusion Models: A Unified Perspective
[2] 一文解释 经验贝叶斯估计, Tweedie’s formula