第二章 搜索 No.2多源bfs，最小步数与双端队列广搜

根据Dijkstra的正确性可以验证bfs的正确性

---

多源bfs：173. 矩阵距离

173. 矩阵距离 - AcWing题库

输出01矩阵中的所有点到1的最短曼哈顿距离，反向思考，求1到图中所有点的最短距离，由于图中可能有多个1，即多个源点。所以这是一题多源bfs问题
与图论中的多源最短路：求任意两点间的最短距离不同，多源bfs求的是多个源点到多个终点中的最近终点距离，即多源bfs的源点与终点所属集合是任意两点间这个集合的子集
考虑将多源问题转换成单源问题，建立虚拟源点，在虚拟源点与其他源点之间建立权值为0的边，那么从虚拟源点到终点的最短距离在数值上与多个源点到终点的最短距离相等

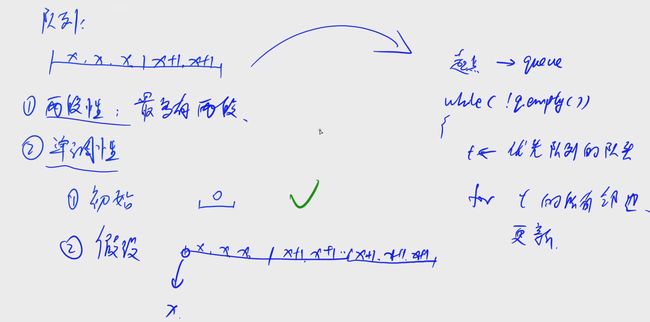
如何用代码实现？假设建立了虚拟源点，将虚拟源点入队，进行bfs。那么第一次扩展，虚拟源点会将其他所有源点入队，并更新它们的最短距离为0（因为源点为1，因此1到1的最短距离为0），然后再用这些源点向外扩展
所以多源最短路与单源最短路是相似的，单源最短路要先将一个源点入队并更新距离，而多源最短路则是将所有源点入队并更新距离

#include 
#include 
using namespace std;

typedef pair<int, int> PII;
const int N = 1010, M = N * N;
PII q[M];
char g[N][N];
int n, m, dis[N][N];

int dx[4] = { 0, 0, -1, 1 }, dy[4] = { 1, -1, 0, 0 };

void bfs()
{
    int tt = -1, hh = 0;
    for (int i = 0; i < n; ++ i )
        for (int j = 0; j < m; ++ j )
            if (g[i][j] == '1')
                q[ ++ tt ] = { i, j }, dis[i][j] = 0;
                
    while (tt >= hh)
    {
        auto t = q[hh ++ ];
        int tx = t.first, ty = t.second;
        for (int i = 0; i < 4; ++ i )
        {
            int nx = tx + dx[i], ny = ty + dy[i];
            if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
            if (dis[nx][ny] != -1) continue;
            dis[nx][ny] = dis[tx][ty] + 1;
            q[ ++ tt ] = { nx, ny }; 
        }
    }
}

int main()
{
    memset(dis, -1, sizeof(dis));
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++ i )
        scanf("%s", g[i]);
    
    bfs();
    for (int i = 0; i < n; ++ i )
    {
        for (int j = 0; j < m; ++ j )
            printf("%d ", dis[i][j]);
        printf("\n");
    }
    return 0;
}

---

最小步数：1107. 魔板

1107. 魔板 - AcWing题库

一般都是用哈希存储，正常的bfs最短路中，用数组下标表示点的编号，数组内容表示最短距离
而最小步数模型中，将整张图看成一个点，那么数组下标肯定无法很好地表示一张图。可以使用unordered_map，将点的状态表示成first，与源点的最短距离表示成second
而最小步数的难点在于：如何表示每个点的状态？
这道题中，点的状态是一个二维矩阵的信息，一般情况都是将二维矩阵转换成一维，用string表示状态
所以这道题用unordered表示最短距离，由于还需要输出递达最短距离的操作步骤，所以需要保存递达每一个点的前一个点，以及前一个点变换成当前点经过的操作
这里用unordered> last表示

这道题的矩阵一共有三种变换，起始序列为$1,2,3,4,5,6,7,8$，题目给定终止序列，问是否能经过三者变换递达终止序列，如果能，最小的操作次数为多少？
以起始序列为源点，每次变换都能递达其他序列。现在的问题是如何变换矩阵？
起始序列为1 2 3 4 5 6 7 8
经过第一种变换的序列为：8 7 6 5 4 3 2 1
经过第二种变换的序列为：4 1 2 3 6 7 8 5
经过第三种变换的序列为：1 7 2 4 5 3 6 8
不要将序列种的数字理解为序列的数值，将它们理解为原序列的下标。比如这个序列8 7 6 5 4 3 2 1，第一个位置上的数为原序列第8个数，第二个位置上的数为原序列第7个数…
这样理解，矩阵变换就很好实现了

至于说最小字典序输出，只要保证每次bfs扩展时，矩阵按照先进行A变换，再B最后C的扩展顺序即可

#include 
#include 
#include 
#include 
#include 
using namespace std;

queue<string> q;
string start = "12345678", ed;
unordered_map<string, int> dis;
unordered_map<string, pair<string, char>> last;
string ops[3] = { "87654321", "41236785", "17245368" };

string change(string t, int op)
{
    string res;
    for (int i = 0; i < 8; ++ i )
        res += t[ops[op][i] - '1'];
    return res;
}

void bfs()
{
    q.push(start);
    dis[start] = 0;
    while (q.size())
    {
        auto t = q.front();
        if (t == ed) return;
        q.pop();
        for (int i = 0; i < 3; ++ i )
        {
            string u = change(t, i);
            if (!dis.count(u))
            {
                dis[u] = dis[t] + 1;
                last[u] = { t, i + 'A' };
                q.push(u);
            }
        }
    }
}

int main()
{
    int x;
    while (cin >> x)
        ed += x + '0';

    bfs();
    printf("%d\n", dis[ed]);
    string ans;
    while (ed != start)
    {
        ans += last[ed].second;
        ed = last[ed].first;
    }
    reverse(ans.begin(), ans.end());
    if (ans.size()) cout << ans << endl;
    return 0;
}

---

双端队列bfs：175. 电路维修

175. 电路维修 - AcWing题库

双端队列bfs，针对只有0和1的图
题目用符号表示单元格，思考如何建图
一个单元格中，从左上走到右下，若单元格为\，此时的边权为0，否则为1
从右上走到左下，若单元格为/，此时的边权为0，否则为1
权值为1表示需要转动该单元格，才能通过

那么要从当前单元格递达下一单元格（一共四个），可以将单元格看成图中的两点，边的权重取决于两个单元格的电缆方向
可以先建图，处理出图中所有单元格的关系，然后跑最短路。也可以用双端队列进行bfs

不过用来bfs的不是单元格的坐标，而是接点的坐标，用单元格bfs会比较复杂，不大好考虑。单元格直接的电缆有多种情况，需要枚举多次，容易出错
用接点进行bfs呢，只要判断当前接点于下一节点间能够连通的电缆，将其与单元格的电缆进行比对即可
单元格坐标与节点坐标的关系：与左上角的接点坐标相同

#include 
#include 
#include 
using namespace std;

typedef pair<int, int> PII;
const int N = 510;
char g[N][N];
bool st[N][N]; int dis[N][N];

int dx[4] = { 1, 1, -1, -1}, dy[4] = { 1, -1, -1, 1 }; // 下一接点的坐标方向
int dgx[4] = { 0, 0, -1, -1}, dgy[4] = { 0, -1, -1, 0 }; // 下一单元格的坐标方向
char s[10] = "\\/\\/"; // 当前坐标与下一坐标连通的电缆方向
int n, m;

int bfs()
{
    memset(dis, 0x3f, sizeof(dis));
    memset(st, false, sizeof(st));
    deque<PII> q;
    q.push_back({ 0, 0 }); dis[0][0] = 0;
    
    while (q.size())
    {
        auto t = q.front(); q.pop_front();
        int x = t.first, y = t.second; // 当前接点的坐标
        if (st[x][y]) continue;
        st[x][y] = true;
        for (int i = 0; i < 4; ++ i )
        {
            int nx = x + dx[i], ny = y + dy[i];
            if (nx >= 0 && nx <= n && ny >= 0 && ny <= m)
            {
                int gx = x + dgx[i], gy = y + dgy[i];
                int d = dis[x][y] + (s[i] != g[gx][gy]);
                if (dis[nx][ny] > d)
                {
                    dis[nx][ny] = d;
                    if (s[i] != g[gx][gy])  q.push_back({ nx, ny });
                    else q.push_front({ nx, ny });
                }
            }
        }
    }
    return dis[n][m];
}

int main()
{
    
    int T;
    scanf("%d", &T);
    while ( T -- )
    {
        scanf("%d%d", &n, &m); 
        for (int i = 0; i < n; ++ i ) scanf("%s", g[i]);
        int t = bfs();
        if (t == 0x3f3f3f3f) puts("NO SOLUTION");
        else printf("%d\n", t);
    }
    return 0;
}