#64 Abstract Interpretation: Introduction & #66 Galois Connections - 课程笔记
业余民科,阅读笔记,拾人牙慧
前置知识
Operational semantics
TAPL
Opertional semantics specifies the behavior of a programming language by defining a simple abstract machine for it. This machine is “abstract” in the sense that it uses the terms of the language as its machine code, rather that some low-level microprocessor instruction set.
coursera - Compilers and interpreters
TAPL给出的介绍比较抽象,而这个课程给出了关于operational semantics的比较具体的描述。如下图所示,operational semantics使用了类似于transfer function或者type checking中的方式定义了具体的操作语义。term e 1 e_1 e1和term e 2 e_2 e2在相同Context情况下的derivation语义。
进一步地这个abstract machine一般都会有一个 environment 和 store。整个evaluation的结果就是一个term e e e的值和一个新的 s t o r e store store。(这样看你来clang static analyzer就是一个基于operational semantics的abstract machine)
其它
An operational semantics is a mathematical model of programming language execution. It is, in essence, an interpreter defined mathematically. However, an operational semantics is more precise than an interpreter because it is defined mathematically, and not based on the meaning of the programming language in which the interpreter is writen. Operational Semantics
这个pdf的着眼点在mathematical。
另外,operational semantics分为small step和big step。知乎上也有一些简明的解释。
Sound
代码安全角度
我曾经在公司内部的一次分享中给出了在代码安全的角度如何看待 sound 和 complete。
这样描述很直观,但是没有切到问题的本质。
Soundness and Completeness
另外一个我接触到的解释 sound 和 complete 的课程是coursera中的programing languages, Part B的描述。它是从type checking的角度来描述的。
Lecture 39: soundness and completeness
A proof system is sound if everything that is provable is in fact true. In other words, if ϕ 1 , . . . , ϕ n ⊢ ψ \phi_1, ..., \phi_n \vdash \psi ϕ1,...,ϕn⊢ψ then ϕ 1 , . . . , ϕ n ⊨ ψ \phi_1, ..., \phi_n \models \psi ϕ1,...,ϕn⊨ψ.
A proof system is complete if everything that is true has a proof. In other words, if ϕ 1 , . . . , ϕ n ⊨ ψ \phi_1, ..., \phi_n \models \psi ϕ1,...,ϕn⊨ψ then ϕ 1 , . . . , ϕ n ⊢ ψ \phi_1, ..., \phi_n \vdash \psi ϕ1,...,ϕn⊢ψ.
注:“truth” ⊨ \models ⊨, “provability” ⊢ \vdash ⊢
例如我们验证属性 R R R - 程序执行不会遇到空指针解引用,越界,空指针等导致的运行时错误。
- 我们说程序 P P P遵循属性 R R R,如果程序 P P P真的确实遵循属性 R R R,那么就是 sound 的。包含进来的都是符合属性 R R R的程序。
- 我们说程序 P P P不遵循属性 R R R,如果程序 P P P真的不遵循属性 R R R,那么就是complete 的。遵循属性 R R R的程序都能包含进来。
更通俗的解释就是,我本人是一个证明系统,判断 SB 属性。
- 我说 A A A, B B B, C C C, D D D都是 SB,如果他们的确个个儿都是 SB 的话,那我是sound的。我是“保守”的,我是“安全”的,它们不会“上诉”
- 只要“潜在”是 SB 的,我都认为是 SB ,那么我是complete的。我是“自信”的,没有“漏网之鱼”的。
但是这里有一个容易迷惑的地方,上面的属性 R R R是证明程序是安全的,所以站在bug finder的角度来看,不安全的程序,也就是例如存在NPD的程序,可能不存在NPD,也就是存在误报。不安全的程序,那就真的存在bug,有漏报,没误报,是反过来的。
For example, a verification tool is typically called sound if it never misses any errors of the kinds it has been designed to detect, but it is allowed to produce spurious warnings (also called false positives), whereas an automated testing tool is called sound if all reported errors are genuine, but it may miss errors.
What is soundness (in static analysis)?
Partial Order
Definition. A partially ordered set (poset) < S ; ⊑ >
- Reflexive: ∀ a ∈ S : a ⊑ a \forall a \in S : a \sqsubseteq a ∀a∈S:a⊑a
- Antisymmetric: ∀ a , b ∈ S : a ⊑ b ∧ b ⊑ a ⇒ b \forall a, b \in S : a \sqsubseteq b \wedge b \sqsubseteq a \Rightarrow b ∀a,b∈S:a⊑b∧b⊑a⇒b
- Transitive: ∀ a , b , c ∈ S : a ⊑ b ∧ b ⊑ c ⇒ a ⊑ c \forall a, b, c \in S : a \sqsubseteq b \wedge b \sqsubseteq c \Rightarrow a \sqsubseteq c ∀a,b,c∈S:a⊑b∧b⊑c⇒a⊑c
Under-Approximations to Over-Approximations
wiki上在介绍abstract interpretation的时候提到了下面的语句,我以前在描述dataflow analysis的时候也涉及到这个概念。
In computer science, abstract interpretation is a theory of sound approximation of the semantics of computer programs, based on monotonic functions over ordered sets, especially lattice。
这个描述一下子点出了Abstract Interpretation的几个核心要点:
- sound approximation(也就是over approximation)
- monotonic functions
- ordered sets
- lattice
这里介绍一下什么是所谓的sound approximation。相关的概念Over-Approximations,Under-Approximations,Conservative-Approximations和Safe-Approximations。而这些概念和sound和complete又掺和在一起。我的理论知识不是很足,对这个的理解可能并不准确,未来会更新。
As known from Turing and Rice, all nontrivial properties of the behavior of programs written in common programming languages are mathematically undecidable.
I Finding all configurations or behaviours (and hence errors) of arbitrary computer programs can be easily reduced to the halting problem of a Turing machine.
由于Rice’s theorem的存在,我们不可能精确地确定一个程序是否存在属性。但是我们可以对对程序的属性进行 over-approximation 和 under-approximation。林论
Over-Approximations
如下图所示,程序可能存在属性 P P P-不存在NPD,但是我们认为程序拥有更多的属性例如存在NPD。绿色的部分就是over-approximation的部分,如果我们检查的属性是NPD,那么可能NPD就会落在绿色非黄色的区域里,导致误报。
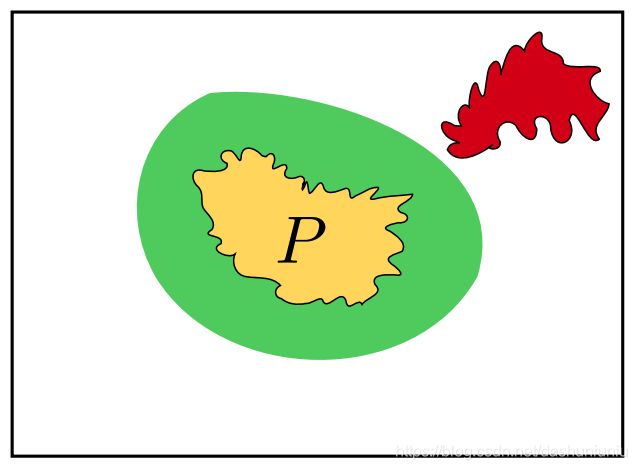
注:上图源于https://www.cis.upenn.edu/~alur/CIS673/isil-plmw.pdf
Under-Approximations

注:上图源于https://www.ida.liu.se/~TDDC90/literature/slides/TDDC90_static_I_handout.pdf
Surjective(满射)
In mathematics, a function f f f from a set X X X to a set Y Y Y is surjective (also known as onto, or a surjection), if for every element y y y in the codomain Y Y Y of f f f, there is at least one element x x x in the domain X X X of f such that f ( x ) = y f(x) = y f(x)=y. - Surjective function
#64 Abstract Interpretation
抽象解释是一个比数据流分析更高层的一个概念,数据流分析是抽象解释的一个特例。我对数据流分析比较熟悉,但是无论是其fixed point还是其termination的保证就是源于抽象解释的理论基础。
抽象解释的特点就是将concrete的operation“降到”一个abstract domain上进行。
如下图所示,原始的operational semantics(使用 → \rightarrow →表示)是在 V V V上进行的,而抽象解释通过 β \beta β将 V V V抽象到abstract domian A A A,而我们现在要做的就是在在abstract domian A A A上进行“运算”(通过 ⊳ \rhd ⊳表示)。
这个视频没有使用用烂的sign analysis来描述,而是使用一个复杂的alias analysis进行描述。
我们前面提到过operational semantics有一个对应的abstract machine,具体细节上会有environment和store。所以对于concrete semantics来说,
- 原始值域使用 σ \sigma σ表示,意思是变量 v v v对应的内置地址 l l l。
- V V V上的 operatioinal semantics,就是下图左侧的两个 derivation rule,语句
v :=new T()evaluate完之后,会得到一个新的store(使用map σ \sigma σ表示),其中 v v v对应到新的地址 l l l。语句v1 := v2evaluate之后,将 σ ( v 2 ) \sigma(v_2) σ(v2) map 到 v 1 v_1 v1上。
对于抽象域 A A A来说,
- A A A使用 s s s表示,意思是变量 v v v可能别名的变量集合 S S S。
- A A A上的operational semantics也就是( ⊳ \rhd ⊳),
v := new T()evaluate完之后,将集合 v {v} v map 到 v v v上。v1 := v2evaluate完之后,将 s ( v 2 ) s(v_2) s(v2)并到 s ( v 1 ) s(v_1) s(v1)上。
而 β \beta β就是将concrete semantics中的 σ \sigma σ对应到 s s s上,对应的规则如下所示,意思是对应任意的 v ′ v' v′来说,如果 σ ( v ′ ) = l \sigma(v')=l σ(v′)=l并且 v ′ ∈ S v' \in S v′∈S,那么如果 σ ( v ) = l \sigma(v) = l σ(v)=l,那么 σ ∈ S \sigma \in S σ∈S。
β p t ( < p , σ > ) = < p , v ↦ S ∣ σ ( v ) = l , v ′ ∈ S ⇔ σ ( v ′ ) = l > \beta_{pt} (
注:上图中右侧第二个推导规则中的 σ \sigma σ应该是 s s s
所以核心如下所示:
- 如何定义抽象值域 A A A
- 如何定义抽象值域 A A A上的operationam semantics
- 将 V V V映射到 A A A上的 β \beta β。
最后教授给出了一个总结,抽象解释目的是将不可解的或者slow的问题转换为不是那么精确但是确定性的问题。而数据流分析从概念上也符合抽象解释的含义。
#66Galois Connections
这个视频通过一个数组越界的例子引出了Galois Connections。如下图所示:
对于上图来说,我们可以将左侧看做concrete,把右侧看做abstract,两者之间的映射由 α \alpha α和 γ \gamma γ表示。注意 α \alpha α存在信息损失,它将{0, 3}和{0, 1, 2, 3}映射成了相同的interval,[0, 3]。
后面关于Galois Connections的性质都与 α \alpha α和 γ \gamma γ这两个函数相关。首先 α \alpha α和 γ \gamma γ有如下图的两个性质,前面的两个性质比较好理解,也就是 α \alpha α和 γ \gamma γ都是单调的。最后一个性质,好像写错了,有理解的请告知。
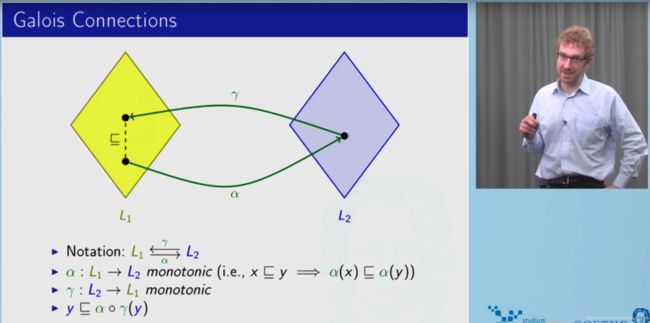
注: α ∘ γ \alpha \circ \gamma α∘γ表示两个函数结合
最后的一个性质应该是 y ⊑ γ ∘ α ( y ) y \sqsubseteq \gamma \circ \alpha(y) y⊑γ∘α(y),也就是经过 y y y经过抽象域这一转换,可能在序上“变大”,这个性质称之为 extensive(没找到中文解释)。
另外一个对应的就是,抽象域的值经过concrete值域这一转换,可能会变小,也就是 α ∘ γ ( x ) ⊑ x \alpha \circ \gamma(x) \sqsubseteq x α∘γ(x)⊑x,这个性质称之为 reductive(同没找到中文解释)。
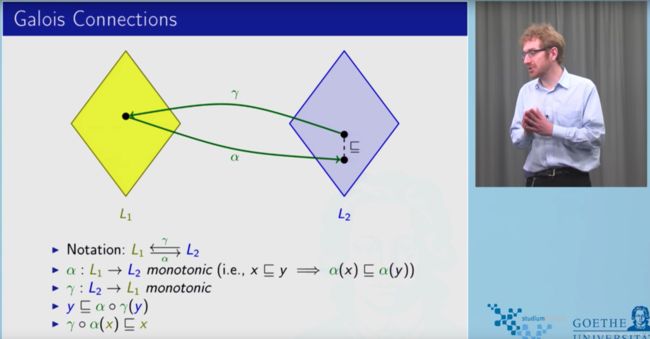
另外该视频还提出了一种,反向从abstract domain计算concrete domian的方法,如下图所示,把所有能够 α ( x ) = [ 0 , 3 ] \alpha(x) = [0, 3] α(x)=[0,3]的值并起来就是最终的结果。
最后总结如下
这个视频给出了一个简单清晰的介绍,但是缺少一些数学上的表示。另外一个更完整的介绍是Abstract Interpretation和Abstract Interpretation
其实Abstract Interpretation是一个很大的话题,可以单独拎出来开一门儿课,后面再介绍关于abstract interpretation中的widening和narrowing等内容
未来待看
Abstract Interpretation in the Operational Semantics Hierarchy
Abstract Interpretation – 40 years back + some years ahead
Abstract Interpretation: Past, Present and Future
Abstract Interpretation
Abstract Interpretation
Abstract Interpretation
Abstract Interpretation
程序分析研究进展
Abstract Interpretation


