leetcode接雨水问题
一、leetcode题目:
11.盛最多水的容器(难度=中等)
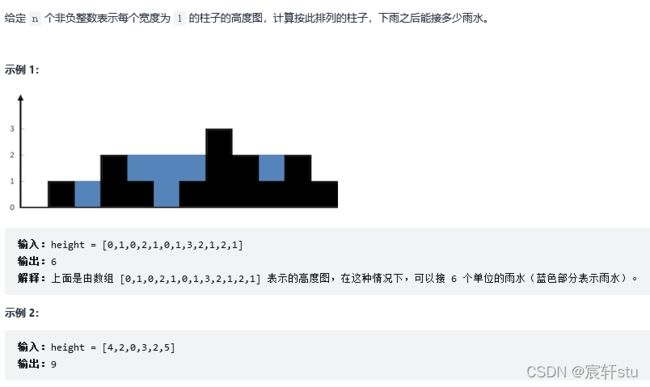
42.接雨水(难度=困难)
407.接雨水II(难度=困难)
二、解题分析:
11.盛最多水的容器
解决方案:双指针法
设两指针 i , j ,指向的水槽板高度分别为 h[i] , h[j] ,此状态下水槽面积为 S(i,j)。由于可容纳水的高度由两板中的 短板 决定,因此可得如下 面积公式 :
S(i,j)=min(h[i],h[j])×(j−i)
在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽 底边宽度 −1-1−1 变短:
若向内 移动短板 ,水槽的短板 min(h[i],h[j])可能变大,因此下个水槽的面积 可能增大 。
若向内 移动长板 ,水槽的短板 min(h[i],h[j])不变或变小,因此下个水槽的面积 一定变小 。
因此,初始化双指针分列水槽左右两端,循环每轮将短板向内移动一格,并更新面积最大值,直到两指针相遇时跳出;即可获得最大面积。
class Solution {
public int maxArea(int[] a) {
int max = 0;
for(int i = 0, j = a.length - 1; i < j ; ){
int minHeight = a[i] < a[j] ? a[i ++] : a[j --]; //注意这里是先赋值,下标再变化
max = Math.max(max, (j - i + 1) * minHeight);
}
return max;
}
}
复杂度分析
时间复杂度:O(N)O(N)O(N),双指针总计最多遍历整个数组一次。
空间复杂度:O(1)O(1)O(1),只需要额外的常数级别的空间。
--------------------------------------------------------------------------------------------------------------
42,接雨水
解决方案:
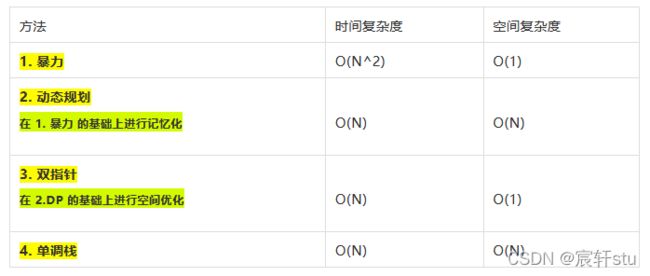
方法1:暴力解法
计算每一根柱子可以存水量,然后所有的加起来就是最终的存水量。其中,每根柱子的存水量等于该柱子左右两侧最大高度中的较小者减去当前柱子的高度。
class Solution {
public int trap(int[] height) {
int res = 0;
// 遍历每个柱子
for (int i = 1; i < height.length - 1; i++) {
int leftMax = 0, rightMax = 0;
// 计算当前柱子左侧的柱子中的最大高度
for (int j = 0; j <= i; j++) {
leftMax = Math.max(leftMax, height[j]);
}
// 计算当前柱子右侧的柱子中的最大高度
for (int j = i; j < height.length; j++) {
rightMax = Math.max(rightMax, height[j]);
}
// 结果中累加当前柱子顶部可以储水的高度,
// 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
res += Math.min(leftMax, rightMax) - height[i];
}
return res;
}
}方法2.动态规划 时间O(N) 空间O(N)
在上述的暴力法中,对于每个柱子,我们都需要从两头重新遍历一遍求出左右两侧的最大高度,这里是有很多重复计算的,很明显最大高度是可以记忆化的,具体在这里可以用数组边递推边存储,也就是常说的动态规划,DP。
class Solution {
public int trap(int[] height) {
int len = height.length;
if(len<=1){
return 0;
}
//dp[i][0]表示 下标i左侧的柱子最大高度
// dp[i][1]表示下标i右侧的柱子最大高度
//当前柱子的存水量= min(dp[i][0],dp[i][1])-height[i]
int[][] dp = new int[len][2];
//初始化
dp[0][0]=height[0];
dp[len-1][1]=height[len-1];
for(int i=1;i=0;i--){
dp[i][1]=Math.max(height[i],dp[i+1][1]);
}
// 遍历每个柱子,累加当前柱子顶部可以储水的高度,
// 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度。
int res=0;
for(int i=1;i 方法3. 双指针法 时间O(N) 空间O(1)
在上述的动态规划方法中,我们用二维数组来存储每个柱子左右两侧的最大高度,但我们递推累加每个柱子的储水高度时其实只用到了 dp[i][0]和 dp[i][1] 两个值,因此我们递推的时候只需要用 int leftMax 和 int rightMax 两个变量就行了。
即将上述代码中的递推公式:
res += Math.min(dp[i][0], dp[i][1]) - height[i];
优化成:
res += Math.min(leftMax, rightMax) - height[i];
注意这里的 leftMax 是从左端开始递推得到的,而 rightMax 是从右端开始递推得到的。因此遍历每个柱子,累加每个柱子的储水高度时,也需要用 left 和 right 两个指针从两端开始遍历。
class Solution {
public int trap(int[] height) {
int res = 0, leftMax = 0, rightMax = 0, left = 0, right = height.length - 1;
while (left <= right) {
if (leftMax <= rightMax) {
leftMax = Math.max(leftMax, height[left]);
res += leftMax - height[left++];
} else {
rightMax = Math.max(rightMax, height[right]);
res += rightMax - height[right--];
}
}
return res;
}
}方法4.单调栈 时间O(N) 空间O(N)
单调栈是本文想要重点说明的一个方法~
因为本题是一道典型的单调栈的应用题。
简单来说就是当前柱子如果小于等于栈顶元素,说明形不成凹槽,则将当前柱子入栈;反之若当前柱子大于栈顶元素,说明形成了凹槽,于是将栈中小于当前柱子的元素pop出来,将凹槽的大小累加到结果中。
具体分析见链接:力扣
class Solution {
public int trap(int[] height) {
Stack stack = new Stack<>();
int res = 0;
// 遍历每个柱体
for (int i = 0; i < height.length; i++) {
while (!stack.isEmpty() && height[stack.peek()] < height[i]) {
int bottomIdx = stack.pop();
// 如果栈顶元素一直相等,那么全都pop出去,只留第一个。
while (!stack.isEmpty() && height[stack.peek()] == height[bottomIdx]) {
stack.pop();
}
if (!stack.isEmpty()) {
// stack.peek()是此次接住的雨水的左边界的位置,右边界是当前的柱体,即i。
// Math.min(height[stack.peek()], height[i]) 是左右柱子高度的min,减去height[bottomIdx]就是雨水的高度。
// i - stack.peek() - 1 是雨水的宽度。
res += (Math.min(height[stack.peek()], height[i]) - height[bottomIdx]) * (i - stack.peek() - 1);
}
}
stack.push(i);
}
return res;
}
}