Chapter 2 Crystal Dynamics 2.2 声子热容
2.2 Phonon Heat Capacity 声子热容
根据热力学第一定律: Δ Q = Δ U + p Δ V \Delta Q= \Delta U + p\Delta V ΔQ=ΔU+pΔV
对于固体: Δ V = 0 \Delta V=0 ΔV=0
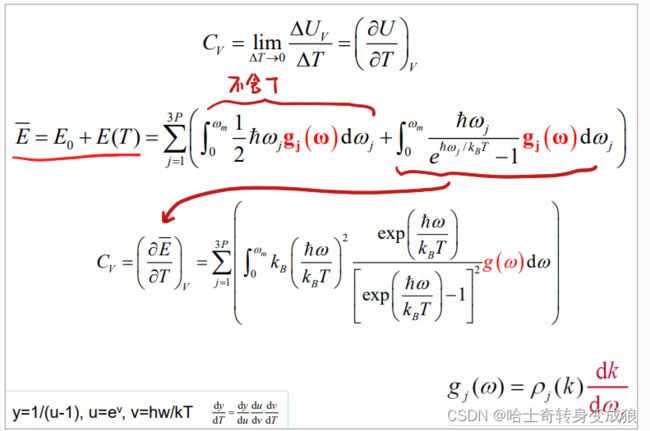
热容 heat capacity: C V = lim Δ T = 0 Δ Q Δ T = lim Δ T = 0 Δ U V Δ T = ( ∂ U ∂ T ) V C_V = \lim _{\Delta T=0} \frac{\Delta Q}{\Delta T} = \lim _{\Delta T=0} \frac{\Delta U_V}{\Delta T} = \left ( \frac{\partial U}{\partial T}\right )_V CV=ΔT=0limΔTΔQ=ΔT=0limΔTΔUV=(∂T∂U)V
The energy in a solid includes:
- the energy given to lattice vibrations - dominant contribution to the heat capacity in most solids.
- the energy given to electron’s movement. 电子运动热容对于大部分常温下的固体来说都可以忽略
Calculation of the lattice energy and heat capacity of a solid falls into two steps:
- the evaluation of the contribution of lattice waves with the frequency of ω
- the summation over all frequency distribution of lattice waves
按照先求态密度再求晶格振动总能量的思路,最终落脚到求晶体的色散关系上,即求 d k d ω \frac{d k}{d \omega} dωdk,但是大多数晶体的色散关系都需要实验测出,且比较复杂,所以需要其他的模型来算。
2.2.1 Dulong-Petit Law 杜隆-珀蒂定律
(1)能量均分学说 Energy equipartition theorem
translation motion: ϵ k − T r a n s l a t i o n = 1 2 m v 2 ‾ = 3 2 k T \epsilon_{k-Translation} = \frac{1}{2}m \overline{ v^2} = \frac{3}{2}kT ϵk−Translation=21mv2=23kT
∵ v x 2 ‾ = v y 2 ‾ = v z 2 ‾ = 1 3 v 2 ‾ \because \overline{v_x^2} =\overline {v_y^2} = \overline {v_z^2} = \frac{1}{3} \overline{ v^2} ∵vx2=vy2=vz2=31v2
1 2 m v x 2 ‾ = 1 2 m v y 2 ‾ = 1 2 m v z 2 ‾ = 1 2 k T \frac{1}{2}m \overline {v_x^2 }=\frac{1}{2}m\overline {v_y^2}=\frac{1}{2}m \overline{v_z^2}=\frac{1}{2}kT 21mvx2=21mvy2=21mvz2=21kT
根据能量均分理论 theorem of equipartition of energy:
The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per degree of freedom in the translational motion of a molecule should equal that of its rotational motions.
能量按照自由度均分。
分子平移运动中每自由度的平均动能应该等于其旋转运动的平均动能。
rotation and vibration:
Kinetic energy of a molecule with translation freedom degree t(平动), rotation freedom degree r(转动)and vibration freedom degree s(振动)
ϵ k ‾ = 1 2 ( t + r + s ) k T \overline{\epsilon _k} = \frac{1}{2}(t+r+s)kT ϵk=21(t+r+s)kT
仅考虑简谐振动,动能=势能
total energy:
ϵ t o t a l ‾ = 1 2 ( t + r + s ) k T + 1 2 s k T \overline{\epsilon_{total}} = \frac{1}{2} (t+r+s)kT + \frac{1}{2}skT ϵtotal=21(t+r+s)kT+21skT
最后一项是振动势能(simple harmonic vibration)
单原子分子(monatomic molecule) t=3, r=s=0 ϵ t o t a l ‾ = 3 2 k T \overline{\epsilon_{total}} = \frac{3}{2}kT ϵtotal=23kT
双原子分子(diatomic molecule) t=3, r=2, s=1 ϵ t o t a l ‾ = 7 2 k T \overline{\epsilon_{total}} = \frac{7}{2}kT ϵtotal=27kT
(2)理想气体的热容 Heat capacity of ideal gas
气体常数: R = N A k = 8.314 J / ( m o l ⋅ k ) R= N_A k = 8.314 J/(mol \cdot k) R=NAk=8.314J/(mol⋅k)
理想气体: E m o l = ϵ t o t a l ‾ N A = 1 2 ( t + r + 2 s ) N A k T = 1 2 ( t + r + 2 s ) R T E^{mol} = \overline{\epsilon _{total}} N_A = \frac{1}{2}(t+r+2s) N_A k T = \frac{1}{2}(t+r+2s)RT Emol=ϵtotalNA=21(t+r+2s)NAkT=21(t+r+2s)RT
定容热容: C V m o l = d E m o l d T = 1 2 ( t + r + 2 s ) R C_V^{mol} = \frac{d E^{mol}}{d T} = \frac{1}{2} (t+r+2s)R CVmol=dTdEmol=21(t+r+2s)R
(3)固体热容3R Heat capacity of solid/ Dulong-Petit Law
延续理想气体热容公式。
对于固体来说, t=0, r=0, s=3,所以有: ϵ i ‾ = 3 2 k B T \overline{\epsilon_i} = \frac{3}{2}k_BT ϵi=23kBT
对于简单的谐振振动来说: ϵ p i ‾ = ϵ i ‾ \overline{\epsilon_{pi}} = \overline{\epsilon_i} ϵpi=ϵi
1mol 固体状态物质的总能量: E = N A ( ϵ p i ‾ + ϵ i ‾ ) = 3 N A k B T = 3 R T E =N_A ( \overline{\epsilon_{pi}} +\overline{\epsilon_i} ) = 3N_A k_B T = 3RT E=NA(ϵpi+ϵi)=3NAkBT=3RT
Molar heat capacity of solid state matter ( Dulong-Petit Law ):
C V m o l = ∂ E ∂ T = 3 N A k B = 3 R = 24.9 ( J / m o l ⋅ K ) = 6 ( c a l / m o l ⋅ K ) C_V^{mol} = \frac{\partial E}{\partial T} = 3N_A k_B = 3R = 24.9 (J/mol\cdot K) = 6 (cal/ mol \cdot K) CVmol=∂T∂E=3NAkB=3R=24.9(J/mol⋅K)=6(cal/mol⋅K)
This law states that the mole specific heat of any solid is independent of temperature and is the same for all materials! At high temperatures, all crystalline solids have a specific heat of 25J/K (or 6cal/K) per mole.
PROBLEM of Dulong-Petit Law :
- 对于钻石、硅、硼不适用;
- 室温和低温情况下不适用。At room temperatures and below, the specific heat of solids is not a universal constant and decreases towards zero.
2.2.2 Einstein Heat Capacity Model 爱因斯坦热容模型
(1)假设 assumption
E ˉ = ∑ i E i ‾ = ∑ i ( 1 2 + 1 e ℏ ω i / k B T − 1 ) ℏ ω i = ∑ i 1 2 ℏ ω i + ∑ i ℏ ω i e ℏ ω i / k B T − 1 \bar E = \sum_i \overline{E_i} = \sum_i \left( \frac{1}{2} + \frac{1}{e^{\hbar \omega_i / k_B T} -1} \right ) \hbar \omega_i = \sum_i \frac{1}{2} \hbar \omega_i + \sum_i \frac{\hbar \omega_i}{e^{\hbar \omega_i / k_B T} - 1} Eˉ=i∑Ei=i∑(21+eℏωi/kBT−11)ℏωi=i∑21ℏωi+i∑eℏωi/kBT−1ℏωi
ω = ω 0 = c o n s t \omega = \omega_0 = const ω=ω0=const
If a solid contains N atoms, the total lattice vibration energy can be written as:
E ˉ = 3 N 2 ℏ ω 0 + 3 N ℏ ω 0 e ℏ ω 0 / k B T − 1 \bar E = \frac{3N}{2}\hbar \omega_0 + \frac{3N\hbar \omega_0}{e^{\hbar \omega_0/ k_B T} - 1} Eˉ=23Nℏω0+eℏω0/kBT−13Nℏω0
Heat capacity: 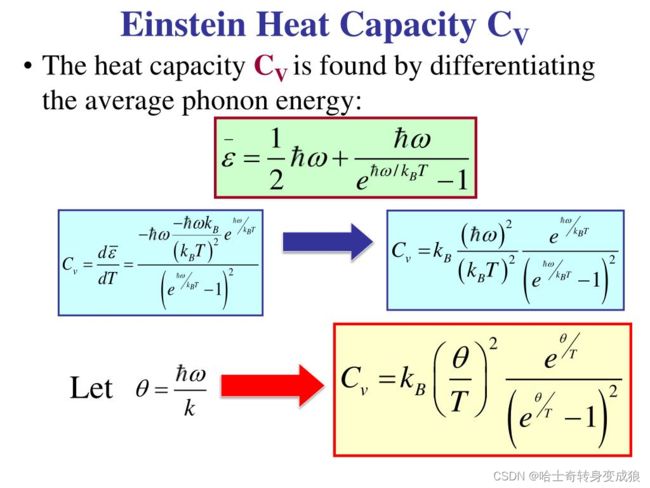
In this model, the atoms are treated as independent oscillators, but the energy of the oscillators are taken quantum mechanically as phonons.
Einstein temperature: Θ E = ℏ ω 0 k B \Theta _E = \frac{\hbar \omega_0}{k_B} ΘE=kBℏω0
(2)讨论 discussion
High and Low Temperature Limits for Einstein Model

(3)问题 problem
a c t u a l : C V ∝ T 3 actual: C_V \propto T^3 actual:CV∝T3
E i n s t e i n : C V ∝ e T Einstein: C_V \propto e^T Einstein:CV∝eT
A correct C V C_V CV tendence to zero at 0K, but an incorrect temperature dependence near 0K.
问题核心:所有格波频率相同 the assumption of all lattice waves having the same frequency
2.2.3 Debye Heat Capacity Model 德拜热容模型
(1)假设
核心假设:在低温下,只有低频振动才能从基态中激发出来,即低温下只有低频格波对晶体热容有贡献。At low T’s, only lattice waves with low frequencies can be excited from their ground states.
低频长波格波可视作连续介质中的弹性波(sound waves),具有线性关系 ω = c k \omega = c k ω=ck,从而可以得到波速度: ∣ Δ k ω ∣ = ∣ d ω d k ∣ = c = c o n s t |\Delta_k \omega| = \left | \frac{d\omega}{d k} \right| = c =const ∣Δkω∣= dkdω =c=const
In the Debye approximation, the velocity of lattice wave is taken as a constant, as it would be for a classical elastic continuum.
声学支在 k → 0 k \rightarrow 0 k→0时,可以用简单的线性关系刻画 ω ( k ) \omega(k) ω(k)。
对于一维双原子链: k → 0 , ω − ≈ 1 2 a 2 β M + m ⋅ k ∝ k k \rightarrow 0, \ \ \ \omega_- \approx \frac{1}{2}a \sqrt{ \frac{2\beta}{M+m}} \cdot k \propto k k→0, ω−≈21aM+m2β⋅k∝k
三维情况下处理方法类似,忽略光学支的色散关系,将三个声学支的色散关系近似为线性关系。
(2)Debye T 3 T^3 T3 law, Methods of Debye model
ω D \omega_D ωD:德拜截止频率 Debye frequency or cutoff frequency, ∫ 0 ω D g j ( ω ) d ω = N \int_0^{\omega_D} g_j(\omega) d \omega = N ∫0ωDgj(ω)dω=N
N为声学支独立格波数量
对于3D晶体: ∫ 0 ω D g j ( ω ) d ω = 3 N \int_0^{\omega_D} g_j(\omega) d \omega = 3N ∫0ωDgj(ω)dω=3N
可以得到: ω D = ( 6 π 2 N V ) 1 / 3 ν \omega_D = \left ( 6\pi^2 \frac{N}{V} \right)^{1/3}\nu ωD=(6π2VN)1/3ν
g ( ω ) = { ∑ j = 1 3 g j ( ω ) = 9 N ω 2 ω D 3 , if ω ≤ ω D 0 , if ω > ω D g(\omega) = \begin{cases} \sum_{j=1}^3 g_j(\omega) = 9N\frac{\omega^2}{\omega_D^3}, & \text{if } \omega \le \omega_D \\ 0, & \text{if }\omega > \omega_D \end{cases} g(ω)={∑j=13gj(ω)=9NωD3ω2,0,if ω≤ωDif ω>ωD
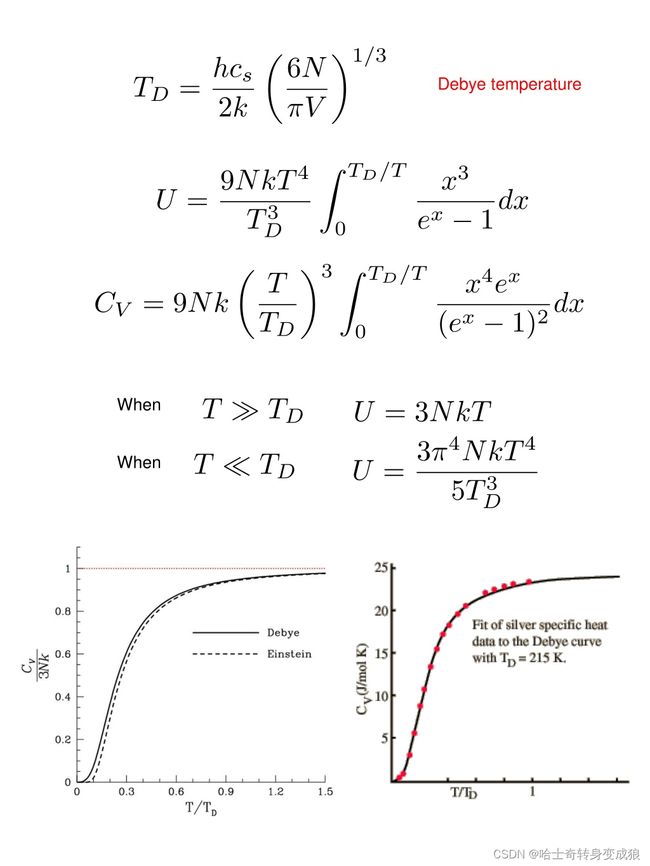
Debye Temperature T D = Θ D = ℏ ω D k B T_D=\Theta_D = \frac{\hbar \omega_D}{k_B} TD=ΘD=kBℏωD
In Debye model, the heat capacity of solids varies as T 3 T^3 T3 at low temperature. This is referred to as Debye T 3 T^3 T3 law.
- The Debye model gives quite a good representation of the heat capacity of most solids.
- For actual crystals, the temperatures at which the T3 approximation holds are quite low (~ T = Θ D / 50 = T D / 50 T=\Theta_D/50 = T_D/50 T=ΘD/50=TD/50)
德拜截止频率和德拜温度反应了固体中的声速。所以具有低密度和大弹性模量的固体具有更高的德拜温度。