机器人研究方向的自我学习[5] 操作臂雅克比：速度与静力及其MATLAB仿真

1、基础知识

之前学习的机械臂只是静态定位，之后将会学习机械臂的动态位置变化。

1.1 位置矢量的导数

标量的导数直接求导，而矢量的导数需要借助坐标系对方向进行描述。
通常描述一点的速度取决于两个坐标系：**一个是先进行求导的坐标系，另一个是描述这个速度矢量的坐标系。**如：

表示相对于A坐标系的在坐标系B中Q点的速度。

1.2角速度矢量

线速度描述了点的属性，角速度则描述了刚体的一种属性。坐标系总是固定在被描述的刚体上，所以用角速度来描述坐标系的旋转运动。同理：

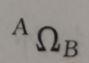
表示坐标系B相对于坐标系A的旋转。方向就是旋转轴的方向，大小表示旋转速率。

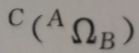
表示坐标系B相对于坐标系A旋转的角速度在坐标系C中的描述。

1.3 线速度

假定坐标系B相对坐标系A的方向不变，则坐标系A中Q点的速度为

1.4角速度

两坐标系原点重合、相对线速度为零。
如果系统是旋转的那么从固定坐标系A看坐标系B中的Q位置矢量，这个矢量如何变化？
即点 Q的速度矢量加上B相对于A的角速度矢量乘以Q的位置矢量。

利用旋转矩阵消掉上标后

以此扩展到原点不重合，且有线速度的情况：

2、机器人连杆的运动

vi表示连杆坐标系i原点的线速度，wi表示连杆坐标系i的角速度

2.1 连杆之间的速度传递

操作臂是一个链式结构，连杆i+1的速度就是连杆i的速度加上那些由关节i+1引起的新的速度分量。

根据以上公式做题：

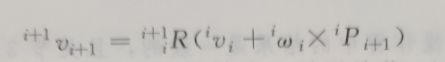
3、雅克比

3.1 雅可比矩阵

在向量微积分中，雅可比矩阵是一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式

在机器人学中，通常使用雅可比将关节速度和操作臂末端的笛卡尔速度联系起来。

雅可比矩阵的行数等于操作臂在笛卡尔空间中的自由度数量，列数等于操作臂关节的数量。

因此上面的例题可以写出一个2*2的雅克比矩阵将关节速度和末端执行器的速度联系起来

雅可比矩阵参考坐标系的转换：

坐标系之间速度的转换

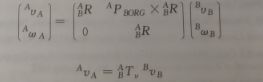
坐标系之间静力的转换

3.2 奇异性

已知一个线性变换可以把关节速度和笛卡尔联系起来，就会有一个问题：这个线性变换是可逆的吗？

若这个式子成立，则机械手在笛卡尔空间的速度已知则可以计算出沿着这个路径所需要的关节速度。

大多数操作臂都有使得雅可比矩阵奇异的Θ值。这个位置就称为机构的奇异位形或者简称奇异性。

例如：
1、操作臂完全展开或者收回使得末端执行器处于或者非常接近工作空间边界的情况。
2、总是远离工作空间的边界，通常是由于两个或者两个以上关节轴共线引起的。

当操作臂处于奇异位形时，它会失去或多个自由度，这时，无论选择怎样的关节速度都不能使机器人手臂移动。

4.操作臂的静力

当机械手抓住某个负载时我们希望求出保持系统静态平衡的关节力矩。
先不考虑操作臂连杆的重力。

如图：

若使系统平衡则应满足下列方程：

加上坐标系转换：

例题:

这与前面关节速度和操作臂末端的笛卡尔速度联系起来的雅可比矩阵互为转置，这不是巧合。

笛卡尔空间的解释

雅可比矩阵的转置将作用在手臂上的笛卡尔力映射成了等效关节力矩。

5.雅可比矩阵参考坐标系的变换

6.习题

程序：

clc
clear
%建立模型
L(1)= Link('d', 0, 'a', 0, 'alpha', 0);
L(2)= Link('d', 0, 'a', 4, 'alpha', 0);
L(3)= Link('d', 0, 'a', 3, 'alpha', 0);
robot=SerialLink([L(1),L(2),L(3)],'name','t');   %SerialLink 类函数 %连接连杆
robot.name='三连杆平面机械臂';
robot.comment='三连机械臂';
robot.display();    %Link类函数，显示建立机器人DH参数
Q=robot.fkine([pi/2,pi/2,pi/2]);%正运动学
%基本参数
L1=4;
L2=3;
L3=2;

Fx=1;
Fy=2;
Mz=3;

a(1)=10;
b(1)=20;
c(1)=30;

x=0.2;
y=-0.3;
w=-0.2;

%开始循环
for i=1:6
    t=0;
    if t<0.6

        %{0}坐标系雅克比
        J=[-L1*sind(a(i))-L2*sind(a(i)+b(i))-L3*sind(a(i)+b(i)+c(i))   -L2*sind(a(i)+b(i))-L3*sind(a(i)+b(i)+c(i)) -L3*sind(a(i)+b(i)+c(i));
           L1*cosd(a(i))+L2*cosd(a(i)+b(i))+L3*cosd(a(i)+b(i)+c(i))  L2*cosd(a(i)+b(i))+L3*cosd(a(i)+b(i)+c(i))   L3*cosd(a(i)+b(i)+c(i));
                 1                                     1                        1;];
        
         %计算关节力矩
        q1(i)=J(1,1)*Fx+J(1,2)*Fy+J(1,3)*Mz;
        q2(i)=J(2,1)*Fx+J(2,2)*Fy+J(2,3)*Mz;
        q3(i)=J(3,1)*Fx+J(3,2)*Fy+J(3,3)*Mz;
        
        %绘制操作臂运动图
        fig=figure(i);
        %subplot(2,3,i);%放在一张图
        theta=[a(i) b(i) c(i)];  
        robot.plot(theta);
        %单张图片保存
        %  frame = getframe(fig); % 获取frame
        % img = frame2im(frame); % 将frame变换成imwrite函数可以识别的格式
        % imwrite(img,[num2str(i),'.jpg']); % 保存到工作目录下，名字为"i.png"
       
        %制作GIF
        filename = 'test.gif';
        drawnow        %每进行一次plot指令便循环一次
        frame = getframe(fig); 
        im = frame2im(frame); 
        [imind,cm] = rgb2ind(im,256);
        if i == 1    
            imwrite(imind, cm, filename, 'gif', 'Loopcount', inf, 'DelayTime', 0.3);
       else                    
            imwrite(imind, cm, filename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.3);
        end       
      % 更新变量
      
        i=i+1;
        t=t+0.1;
        p=inv(J)*[x;y;w];
        a(i)=p(1,1)*180/pi;
        b(i)=p(2,1)*180/pi;
        c(i)=p(3,1)*180/pi;
    end
end   

运行结果：

绘制时间关系图：将上个程序运行的数据进行绘制图形

clc
close
clear
a=[10,-7.40424424530256,14.7127382775927,-6.31176972469085,14.5183299091678,-6.38193264425691];
b=[20,16.4253231875417,-32.6301955793773,16.7135828821396,-32.2933029288375,16.8780907311873];
c=[30,-20.4802348448556,6.45830139916818,-21.8609690600652,6.31581711705328,-21.9553139895469];
q1=[-15.586897556080984,1.488327793070156,4.136958906661944,1.198833486720448,4.128787539765772,1.189127852725739];
q2=[17.733459646108780,24.616121908009422,24.193150590966790,24.588644324556586,24.203434369258634,24.585415138079075];
q3=[6,6,6,6,6,6];
t=[0 0.1 0.2 0.3 0.4 0.50];
aa=a.*t;
bb=b.*t;
cc=c.*t; 
x=0.2.*t;
y=-0.3.*t;
w=-0.2.*t;

L1=4;
L2=3;
L3=2;
          
fig=figure
subplot(2,3,1)
plot(t,a,'r',t,b,'black',t,c,'b');
grid on;title('关节角速率');


subplot(2,3,2)
plot(t,aa,'r',t,bb,'black',t,cc,'b');
grid on;title('关节角');

subplot(2,3,3)
plot(t,q1,'r',t,q2,'black',t,q3,'b');
grid on;title('关节力矩');

subplot(2,3,4)
plot(t,x,'r',t,y,'black',t,w,'b');
grid on;title('xyw');


for i=1:6
    J=[-L1*sind(a(i))-L2*sind(a(i)+b(i))-L3*sind(a(i)+b(i)+c(i))   -L2*sind(a(i)+b(i))-L3*sind(a(i)+b(i)+c(i)) -L3*sind(a(i)+b(i)+c(i));
           L1*cosd(a(i))+L2*cosd(a(i)+b(i))+L3*cosd(a(i)+b(i)+c(i))  L2*cosd(a(i)+b(i))+L3*cosd(a(i)+b(i)+c(i))   L3*cosd(a(i)+b(i)+c(i));
                 1                                     1                        1;];

    k(i)=det(J);
end
subplot(2,3,5)
plot(t,k,'r');
grid on;title('雅克比矩阵行列式');

frame = getframe(fig); % 获取frame
img = frame2im(frame); % 将frame变换成imwrite函数可以识别的格式
imwrite(img,'1.jpg'); % 保存到工作目录下，名字为"i.png"

运行结果：

如果使用系统自带的函数 jacob0() (相对于坐标系{0}）jacobn()(相对于坐标系n)

则结果略有不同： 验证自己编写程序的正确性