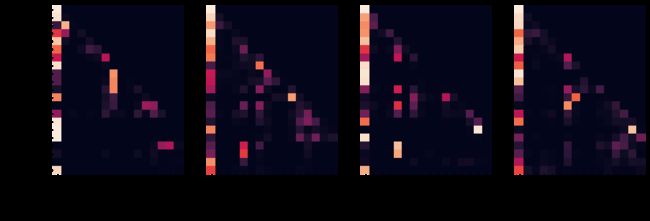The Annotated Transformer

我们不生产水,我们只是大自然的搬运工！

原文地址：
The Annotated Transformer
The Annotated Transformer

The Transformer has been on a lot of people’s minds over the last five years. This post presents an annotated version of the paper in the form of a line-by-line implementation. It reorders and deletes some sections from the original paper and adds comments throughout.

Prelims

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import math, copy, time
from torch.autograd import Variable
import matplotlib.pyplot as plt
import seaborn # 绘图库
seaborn.set_context(context="talk") # 设置图表的风格，线宽字体都变得有些大

Background

The goal of reducing sequential computation also forms the foundation of the Extended Neural GPU, ByteNet and ConvS2S, all of which use convolutional neural networks as basic building block, computing hidden representations in parallel for all input and output positions.

In these models, the number of operations required to relate signals from two arbitrary input or output positions grows in the distance between positions, linearly for ConvS2S and logarithmically for ByteNet. This makes it more difficult to learn dependencies between distant positions.

In the Transformer this is reduced to a constant number of operations, albeit at the cost of reduced effective resolution due to averaging attention-weighted positions, an effect we counteract with Multi-Head Attention.

Self-attention, sometimes called intra-attention is an attention mechanism relating different positions of a single sequence in order to compute a representation of the sequence.

Self-attention has been used successfully in a variety of tasks including reading comprehension, abstractive summarization, textual entailment and learning task-independent sentence representations.

End-to-end memory networks are based on a recurrent attention mechanism instead of sequencealigned recurrence and have been shown to perform well on simple-language question answering and language modeling tasks.

To the best of our knowledge, however, the Transformer is the first transduction model relying entirely on self-attention to compute representations of its input and output without using sequence aligned RNNs or convolution.

Part 1: Model Architecture

Overall Architecture

Most competitive neural sequence transduction models have an encoder-decoder structure.

Here, the encoder maps an input sequence of symbol representations $(x_1,...,x_n)$to a sequence of continuous representations $\mathbf{z}=(z_1,...,z_n)$.

Given $\mathbf{z}$, the decoder then generates an output sequence $(y_1,...,y_m)$of symbols one element at a time.

At each step the model is auto-regressive , consuming the previously generated symbols as additional input when generating the next.

class EncoderDecoder(nn.Module):
    """
    A standard Encoder-Decoder architecture. Base for this and many 
    other models.
    """
    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        super(EncoderDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.src_embed = src_embed
        self.tgt_embed = tgt_embed
        self.generator = generator
        
    def forward(self, src, tgt, src_mask, tgt_mask):
        "Take in and process masked src and target sequences."
        return self.decode(self.encode(src, src_mask), src_mask,
                            tgt, tgt_mask)
    
    def encode(self, src, src_mask):
        return self.encoder(self.src_embed(src), src_mask)
    
    def decode(self, memory, src_mask, tgt, tgt_mask):
        return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)

class Generator(nn.Module):
    "Define standard linear + softmax generation step."
    def __init__(self, d_model, vocab):
        super(Generator, self).__init__()
        self.proj = nn.Linear(d_model, vocab)

    def forward(self, x):
        return F.log_softmax(self.proj(x), dim=-1)

The Transformer follows this overall architecture using stacked self-attention and point-wise, fully connected layers for both the encoder and decoder, shown in the left and right halves of Figure 1, respectively.

Encoder and Decoder Stacks

Encoder

The encoder is composed of a stack of $N=6$ identical layers.

def clones(module, N):
    "Produce N identical layers."
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

class Encoder(nn.Module):
    "Core encoder is a stack of N layers"
    def __init__(self, layer, N):
        super(Encoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
        
    def forward(self, x, mask):
        "Pass the input (and mask) through each layer in turn."
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x)

We employ a residual connection around each of the two sub-layers, followed by layer normalization.

class LayerNorm(nn.Module):
    "Construct a layernorm module (See citation for details)."
    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2

That is, the output of each sub-layer is $\mathrm{LayerNorm}(x+\mathrm{Sublayer}(x))$, where $\mathrm{Sublayer}(x)$ is the function implemented by the sub-layer itself.

We apply dropout to the output of each sub-layer, before it is added to the sub-layer input and normalized.

To facilitate these residual connections, all sub-layers in the model, as well as the embedding layers, produce outputs of dimension $d_{\text{model}}=512$.

class SublayerConnection(nn.Module):
    """
    A residual connection followed by a layer norm.
    Note for code simplicity the norm is first as opposed to last.
    """

    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        "Apply residual connection to any sublayer with the same size."
        return x + self.dropout(sublayer(self.norm(x)))

Each layer has two sub-layers. The first is a multi-head self-attention mechanism, and the second is a simple, position-wise fully connected feed-forward network.

class EncoderLayer(nn.Module):
    "Encoder is made up of self-attn and feed forward (defined below)"

    def __init__(self, size, self_attn, feed_forward, dropout):
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 2)
        self.size = size

    def forward(self, x, mask):
        "Follow Figure 1 (left) for connections."
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        return self.sublayer[1](x, self.feed_forward)

Decoder

The decoder is also composed of a stack of $N=6$ identical layers.

class Decoder(nn.Module):
    "Generic N layer decoder with masking."

    def __init__(self, layer, N):
        super(Decoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)

    def forward(self, x, memory, src_mask, tgt_mask):
        for layer in self.layers:
            x = layer(x, memory, src_mask, tgt_mask)
        return self.norm(x)

In addition to the two sub-layers in each encoder layer, the decoder inserts a third sub-layer, which performs multi-head attention over the output of the encoder stack.

Similar to the encoder, we employ residual connections around each of the sub-layers, followed by layer normalization.

class DecoderLayer(nn.Module):
    "Decoder is made of self-attn, src-attn, and feed forward (defined below)"

    def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
        super(DecoderLayer, self).__init__()
        self.size = size
        self.self_attn = self_attn
        self.src_attn = src_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 3)

    def forward(self, x, memory, src_mask, tgt_mask):
        "Follow Figure 1 (right) for connections."
        m = memory
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
        x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
        return self.sublayer[2](x, self.feed_forward)

We also modify the self-attention sub-layer in the decoder stack to prevent positions from attending to subsequent positions.

This masking, combined with fact that the output embeddings are offset by one position, ensures that the predictions for position $i$ can depend only on the known outputs at positions less than $i$.

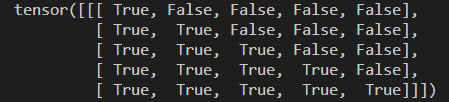
def subsequent_mask(size):
    "Mask out subsequent positions."
    attn_shape = (1, size, size)
    subsequent_mask = torch.triu(torch.ones(attn_shape), diagonal=1).type( # 返回上三角矩阵
        torch.uint8
    )
    return subsequent_mask == 0

Below the attention mask shows the position each tgt word (row) is allowed to look at (column). Words are blocked for attending to future words during training.

plt.figure(figsize=(5,5))
plt.imshow(subsequent_mask(20)[0])
plt.show()
print(subsequent_mask(5))

Attention

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors.

The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.

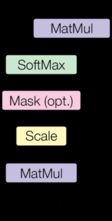
We call our particular attention “Scaled Dot-Product Attention”.

The input consists of queries and keys of dimension $d_k$, and values of dimension $d_v$.

We compute the dot products of the query with all keys, divide each by $\sqrt{d_k}$, and apply a softmax function to obtain the weights on the values.

In practice, we compute the attention function on a set of queries simultaneously, packed together into a matrix $Q$. The keys and values are also packed together into matrices $K$ and $V$. We compute the matrix of outputs as:

$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

def attention(query, key, value, mask=None, dropout=None):
    "Compute 'Scaled Dot Product Attention'"
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9) # 在mask等于0的地方填充一个极小值
    p_attn = scores.softmax(dim=-1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

The two most commonly used attention functions are additive attention , and dot-product (multiplicative) attention.

Dot-product attention is identical to our algorithm, except for the scaling factor of $\frac{1}{\sqrt{d_k}}$.

Additive attention computes the compatibility function using a feed-forward network with a single hidden layer.

While the two are similar in theoretical complexity, dot-product attention is much faster and more space-efficient in practice, since it can be implemented using highly optimized matrix multiplication code.

While for small values of $d_k$ the two mechanisms perform similarly, additive attention outperforms dot product attention without scaling for larger values of $d_k$.

We suspect that for large values of $d_k$, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients (To illustrate why the dot products get large, assume that the components of qq and kk are independent random variables with mean $0$ and variance $1$. Then their dot product, $q\cdot k={\sum }_{i=1}^{d_k}{q}_i{k}_i$, has mean $0$ and variance $d_k$).

To counteract this effect, we scale the dot products by $\frac{1}{\sqrt{d_k}}$ .

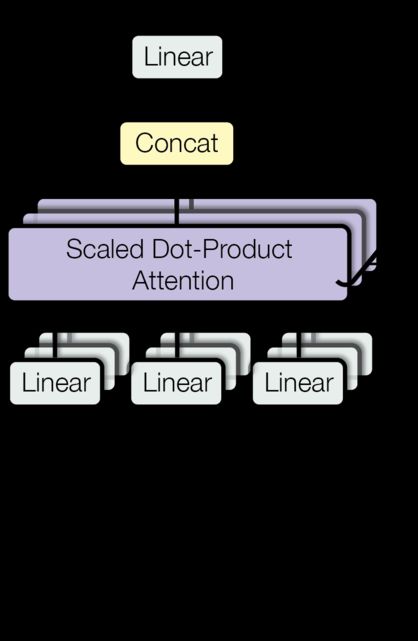
Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.

With a single attention head, averaging inhibits this.

Where the projections are parameter matrices $W_i^Q\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$, $W_i^K\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$, $W_i^V\in {\mathbb{R}}^{d_{\text{model}}\times d_v}$and $W^O\in {\mathbb{R}}^{h{d}_v\times d_{\text{model}}}$.

In this work we employ $h=8$ parallel attention layers, or heads. For each of these we use $d_k=d_v=d_{\text{model}}/h=64$.

Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality.

class MultiHeadedAttention(nn.Module):
    def __init__(self, num_heads, d_model, dropout=0.1):
        "Take in model size and number of heads."
        super(MultiHeadedAttention, self).__init__()
        assert d_model % num_heads == 0 # 无法整除就报异常
        # We assume d_v always equals d_k
        self.d_k = d_model // num_heads # head_size
        self.num_heads = num_heads
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query, key, value, mask=None):
        "Implements Figure 2"
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1) # 添加一个维度
        nbatches = query.size(0)

        # 1) Do all the linear projections in batch from d_model => h x d_k
        query, key, value = [
            lin(x).view(nbatches, -1, self.num_heads, self.d_k).transpose(1, 2)
            for lin, x in zip(self.linears, (query, key, value))
        ]

        # 2) Apply attention on all the projected vectors in batch.
        x, self.attn = attention(
            query, key, value, mask=mask, dropout=self.dropout
        )

        # 3) "Concat" using a view and apply a final linear.
        x = (
            x.transpose(1, 2)
            .contiguous() # Returns a contiguous in memory tensor containing the same data as self tensor.
            .view(nbatches, -1, self.num_heads * self.d_k)
        )
        del query
        del key
        del value
        return self.linears[-1](x)

Applications of Attention in our Model

The Transformer uses multi-head attention in three different ways:

1. In “encoder-decoder attention” layers, the queries come from the previous decoder layer, and the memory keys and values come from the output of the encoder. This allows every position in the decoder to attend over all positions in the input sequence. This mimics the typical encoder-decoder attention mechanisms in sequence-to-sequence models such as .

2. The encoder contains self-attention layers. In a self-attention layer all of the keys, values and queries come from the same place, in this case, the output of the previous layer in the encoder. Each position in the encoder can attend to all positions in the previous layer of the encoder.

3. Similarly, self-attention layers in the decoder allow each position in the decoder to attend to all positions in the decoder up to and including that position. We need to prevent leftward information flow in the decoder to preserve the auto-regressive property. We implement this inside of scaled dot-product attention by masking out (setting to $-\infty$) all values in the input of the softmax which correspond to illegal connections.

Position-wise Feed-Forward Networks

In addition to attention sub-layers, each of the layers in our encoder and decoder contains a fully connected feed-forward network, which is applied to each position separately and identically. This consists of two linear transformations with a ReLU activation in between.

$$FFN(x)=max(0,x{W}_1+b_1)W_2+b_2$$

While the linear transformations are the same across different positions, they use different parameters from layer to layer. Another way of describing this is as two convolutions with kernel size 1.

The dimensionality of input and output is $d_{\text{model}}=512$, and the inner-layer has dimensionality $d_{ff}=2048$.

class PositionwiseFeedForward(nn.Module):
    "Implements FFN equation."
    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(F.relu(self.w_1(x)))) # linear->erlu->dropout->linear->dropout

Embeddings and Softmax

Similarly to other sequence transduction models, we use learned embeddings to convert the input tokens and output tokens to vectors of dimension $d_{\text{model}}$
​
We also use the usual learned linear transformation and softmax function to convert the decoder output to predicted next-token probabilities.

In our model, we share the same weight matrix between the two embedding layers and the pre-softmax linear transformation, similar to.

In the embedding layers, we multiply those weights by $\sqrt{d_{\text{model}}}$

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x):
        return self.lut(x) * math.sqrt(self.d_model)

Positional Encoding

Since our model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence.
​
To this end, we add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks.

The positional encodings have the same dimension $d_{\text{model}}$ as the embeddings, so that the two can be summed. There are many choices of positional encodings, learned and fixed.

In this work, we use sine and cosine functions of different frequencies:

where $pos$ is the position and $i$ is the dimension.

That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from $2\pi$ to $10000\cdot 2\pi$.

We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $P{E}_{pos+k}$ can be represented as a linear function of $P{E}_{pos}$.​.

In addition, we apply dropout to the sums of the embeddings and the positional encodings in both the encoder and decoder stacks. For the base model, we use a rate of $P_{drop}=0.1$.

class PositionalEncoding(nn.Module):
    "Implement the PE function."

    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(
            torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model)
        )
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer("pe", pe)

    def forward(self, x):
        x = x + self.pe[:, : x.size(1)].requires_grad_(False)
        return self.dropout(x)

Below the positional encoding will add in a sine wave based on position. The frequency and offset of the wave is different for each dimension.

plt.figure(figsize=(15, 5))
pe = PositionalEncoding(20, 0)
y = pe.forward(Variable(torch.zeros(1, 100, 20)))
plt.plot(np.arange(100), y[0, :, 4:8].data.numpy())
plt.legend(["dim %d"%p for p in [4,5,6,7]])
plt.show()

We also experimented with using learned positional embeddings instead, and found that the two versions produced nearly identical results. We chose the sinusoidal version because it may allow the model to extrapolate to sequence lengths longer than the ones encountered during training.

Full Model

Here we define a function from hyperparameters to a full model.

def Transformer(src_vocab, tgt_vocab, N=6, 
               d_model=512, d_ff=2048, num_heads=8, dropout=0.1):
    "Helper: Construct a model from hyperparameters."
    c = copy.deepcopy
    mh_attn = MultiHeadedAttention(num_heads, d_model)
    ffn = PositionwiseFeedForward(d_model, d_ff, dropout)
    position = PositionalEncoding(d_model, dropout)
    model = EncoderDecoder(
        Encoder(EncoderLayer(d_model, c(mh_attn), c(ffn), dropout), N),
        Decoder(DecoderLayer(d_model, c(mh_attn), c(mh_attn), c(ffn), dropout), N),
        nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
        nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
        Generator(d_model, tgt_vocab))

    # This was important from their code. 
    # Initialize parameters with Glorot / fan_avg.
    for p in model.parameters():
        if p.dim() > 1:
            nn.init.xavier_uniform(p)
    return model

Inference

Here we make a forward step to generate a prediction of the model. We try to use our transformer to memorize the input. As you will see the output is randomly generated due to the fact that the model is not trained yet. In the next tutorial we will build the training function and try to train our model to memorize the numbers from 1 to 10.

def inference_test():
    test_model = Transformer(11, 11, 2)
    test_model.eval()
    src = torch.LongTensor([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]])
    src_mask = torch.ones(1, 1, 10)

    memory = test_model.encode(src, src_mask)
    ys = torch.zeros(1, 1).type_as(src)

    for i in range(9):
        out = test_model.decode(
            memory, src_mask, ys, subsequent_mask(ys.size(1)).type_as(src.data)
        )
        prob = test_model.generator(out[:, -1])
        _, next_word = torch.max(prob, dim=1)
        next_word = next_word.data[0]
        ys = torch.cat(
            [ys, torch.empty(1, 1).type_as(src.data).fill_(next_word)], dim=1
        )

    print("Example Untrained Model Prediction:", ys)

def run_tests():
    for _ in range(10):
        inference_test()

RUN_EXAMPLES = True

def show_example(fn, args=[]):
    if __name__ == "__main__" and RUN_EXAMPLES:
        return fn(*args)

show_example(run_tests)

Example Untrained Model Prediction: tensor([[0, 4, 6, 3, 4, 6, 3, 4, 6, 3]])
Example Untrained Model Prediction: tensor([[0, 4, 3, 9, 1, 0, 4, 3, 0, 4]])
Example Untrained Model Prediction: tensor([[ 0, 5, 8,1, 9, 10, 0, 5, 8, 8]])
Example Untrained Model Prediction: tensor([[0, 6, 7, 9, 7, 9, 4, 9, 2, 5]])
Example Untrained Model Prediction: tensor([[0, 1, 1, 1, 1, 1, 1, 1, 1, 1]])
Example Untrained Model Prediction: tensor([[ 0, 7, 10, 9, 10, 6, 4, 4, 4, 4]])
Example Untrained Model Prediction: tensor([[0, 3, 2, 7, 2, 6, 6, 6, 6, 6]])
Example Untrained Model Prediction: tensor([[ 0, 7, 4, 2, 4, 2, 4, 2, 4, 10]])
Example Untrained Model Prediction: tensor([[0, 9, 9, 3, 3, 3, 3, 3, 3, 3]])
Example Untrained Model Prediction: tensor([[0, 8, 5, 7, 2, 7, 2, 7, 5, 7]])

Part 2: Model Training

Optimizer

We used the Adam optimizer with ${\beta }_1=0.9$, ${\beta }_2=0.98$ and $ϵ=10^{-9}$. We varied the learning rate over the course of training, according to the formula:

This corresponds to increasing the learning rate linearly for the first $warmup\_steps$ training steps, and decreasing it thereafter proportionally to the inverse square root of the step number. We used $warmup\_steps=4000$.

Note: This part is very important. Need to train with this setup of the model.

Example of the curves of this model for different model sizes and for optimization hyperparameters.

def learn_rate(step, model_size, factor, warmup):
    """
    we have to default the step to 1 for LambdaLR function
    to avoid zero raising to negative power.
    """
    if step == 0:
        step = 1
    return factor * (
        model_size ** (-0.5) * min(step ** (-0.5), step * warmup ** (-1.5))
    )

class NoamOpt:
    "Optim wrapper that implements rate."
    def __init__(self, model_size, factor, warmup, optimizer):
        self.optimizer = optimizer
        self._step = 0
        self.warmup = warmup
        self.factor = factor
        self.model_size = model_size
        self._rate = 0
        
    def step(self):
        "Update parameters and rate"
        self._step += 1
        rate = self.rate()
        for p in self.optimizer.param_groups:
            p['lr'] = rate
        self._rate = rate
        self.optimizer.step()
        
    def rate(self, step = None):
        "Implement `lrate` above"
        if step is None:
            step = self._step
        return self.factor * \
            (self.model_size ** (-0.5) *
            min(step ** (-0.5), step * self.warmup ** (-1.5)))
        
def get_std_opt(model):
    return NoamOpt(model.src_embed[0].d_model, 2, 4000,
            torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))

# Three settings of the lrate hyperparameters.
opts = [NoamOpt(512, 1, 4000, None), 
        NoamOpt(512, 1, 8000, None),
        NoamOpt(256, 1, 4000, None)]
plt.plot(np.arange(1, 20000), [[opt.rate(i) for opt in opts] for i in range(1, 20000)])
plt.legend(["512:4000", "512:8000", "256:4000"])
plt.show()

Attention Visualization

Even with a greedy decoder the translation looks pretty good. We can further visualize it to see what is happening at each layer of the attention

# !wget https://s3.amazonaws.com/opennmt-models/en-de-model.pt

def greedy_decode(model, src, src_mask, max_len, start_symbol):
    memory = model.encode(src, src_mask)
    ys = torch.ones(1, 1).fill_(start_symbol).type_as(src.data)
    for i in range(max_len-1):
        out = model.decode(memory, src_mask, 
                           Variable(ys), 
                           Variable(subsequent_mask(ys.size(1))
                                    .type_as(src.data)))
        prob = model.generator(out[:, -1])
        _, next_word = torch.max(prob, dim = 1)
        next_word = next_word.data[0]
        ys = torch.cat([ys, 
                        torch.ones(1, 1).type_as(src.data).fill_(next_word)], dim=1)
    return ys
    
model, SRC, TGT = torch.load("en-de-model.pt")

model.eval()
sent = "▁The ▁log ▁file ▁can ▁be ▁sent ▁secret ly ▁with ▁email ▁or ▁FTP ▁to ▁a ▁specified ▁receiver".split()
src = torch.LongTensor([[SRC.stoi[w] for w in sent]])
src = Variable(src)
src_mask = (src != SRC.stoi[""]).unsqueeze(-2)
out = greedy_decode(model, src, src_mask, 
                    max_len=60, start_symbol=TGT.stoi[""])
print("Translation:", end="\t")
trans = " "
for i in range(1, out.size(1)):
    sym = TGT.itos[out[0, i]]
    if sym == "": break
    trans += sym + " "
print(trans)

tgt_sent = trans.split()
def draw(data, x, y, ax):
    seaborn.heatmap(data, 
                    xticklabels=x, square=True, yticklabels=y, vmin=0.0, vmax=1.0, 
                    cbar=False, ax=ax)
    
for layer in range(1, 6, 2):
    fig, axs = plt.subplots(1,4, figsize=(20, 10))
    print("Encoder Layer", layer+1)
    for h in range(4):
        draw(model.encoder.layers[layer].self_attn.attn[0, h].data, 
            sent, sent if h ==0 else [], ax=axs[h])
    plt.show()
    
for layer in range(1, 6, 2):
    fig, axs = plt.subplots(1,4, figsize=(20, 10))
    print("Decoder Self Layer", layer+1)
    for h in range(4):
        draw(model.decoder.layers[layer].self_attn.attn[0, h].data[:len(tgt_sent), :len(tgt_sent)], 
            tgt_sent, tgt_sent if h ==0 else [], ax=axs[h])
    plt.show()
    print("Decoder Src Layer", layer+1)
    fig, axs = plt.subplots(1,4, figsize=(20, 10))
    for h in range(4):
        draw(model.decoder.layers[layer].self_attn.attn[0, h].data[:len(tgt_sent), :len(sent)], 
            sent, tgt_sent if h ==0 else [], ax=axs[h])
    plt.show()