一、算法
1.1、算法基础
概念:算法是独⽴存在的⼀种解决问题的⽅法和思想
算法的特性:
- 输入:算法具有0个或多个输⼊
- 输出: 算法⾄少有1个或多个输出
- 有穷性: 算法在有限的步骤之后会⾃动结束⽽不会⽆限循环,并且每⼀个步骤可以在可接受的时间内完成
- 确定性:算法中的每⼀步都有确定的含义,不会出现⼆义性
- 可⾏性:算法的每⼀步都是可⾏的,也就是说每⼀步都能够执⾏有限的次数完成
1.2、算法效率衡量
| ⼤O记法 | 对于单调的整数函数f,如果存在⼀个整数函数g和实常数c>0,使得对于充分⼤的n总有f(n)<=c*g(n),就说函数g是f的⼀个渐近函数(忽略常数),记为f(n)=O(g(n))。也就是说,在趋向⽆穷的极限意义下,函数f的增⻓速度受到函数g的约束,亦即函数f与函数g的特征相似 |
| 时间复杂度 | 假设存在函数g,使得算法A处理规模为n的问题示例所⽤时间为T(n)=O(g(n)),则称O(g(n))为算法A的渐近时间复杂度,简称时间复杂度,记为T(n) |
理解“⼤O记法”
对于算法的时间性质和空间性质,最重要的是其数量级和趋势,这些是分析
算法效率的主要部分。⽽计量算法基本操作数量的规模函数中那些常量因⼦
可以忽略不计。例如,可以认为3n^2 和100n^2 属于同⼀个量级,如果两个算法
处理同样规模实例的代价分别为这两个函数,就认为它们的效率“差不多”,
都为n^2 级
| 复杂度分类 | 解释说明 | 分析哪个复杂度为最优 |
|---|---|---|
| 最优时间复杂度 | 算法完成⼯作最少需要多少基本操作 | 价值不⼤,因为它没有提供什么有⽤信息,其反映的只是最乐观最理想的情况,没有参考价值 |
| 最坏时间复杂度 | 算法完成⼯作最多需要多少基本操作 | 提供了⼀种保证,表明算法在此种程度的基本操作中⼀定能完成⼯作 |
| 平均时间复杂度 | 算法完成⼯作平均需要多少基本操作 | 对算法的⼀个全⾯评价,因此它完整全⾯的反映了这个算法的性质。但另⼀⽅⾯,这种衡量并没有保证,不是每个计算都能在这个基本操作内完成。⽽且,对于平均情况的计算,也会因为应⽤算法的实例分布可能并不均匀⽽难以计算 |
因此,只需关注算法的最坏情况,亦即最坏时间复杂度
时间复杂度的计算规则:
1.基本操作,即只有常数项,认为其时间复杂度为O(1)
2.顺序结构,时间复杂度按加法进⾏计算
3.循环结构,时间复杂度按乘法进⾏计算
4.分⽀结构,时间复杂度取最⼤值
5.判断⼀个算法的效率时,往往只需要关注操作数量的最⾼次项,其它次要项和常数项可以忽略
6.在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度
空间复杂度S(n)
空间复杂度(SpaceComplexity)是对⼀个算法在运⾏过程中临时占⽤存储空间⼤⼩的量度
算法的时间复杂度和空间复杂度合称为算法的复杂度
1.3、常见的时间复杂度
| 执行次数函数 | 阶 | 非正式术语 |
|---|---|---|
| 100 | O(1) | 常数阶 |
| 2n+1 | O(n) | 线性阶 |
| 3n²+2n+1 | O(n²) | 平方阶 |
| 4n³+3n²+2n+1 | O(n³) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
| 5log2n + 1 | O(logn) | 对数阶 |
| 3nlog2n + 2n + 1 | O(nlogn) | nlogn阶 |
注意,将log2n(以2为底的对数)简写成logn
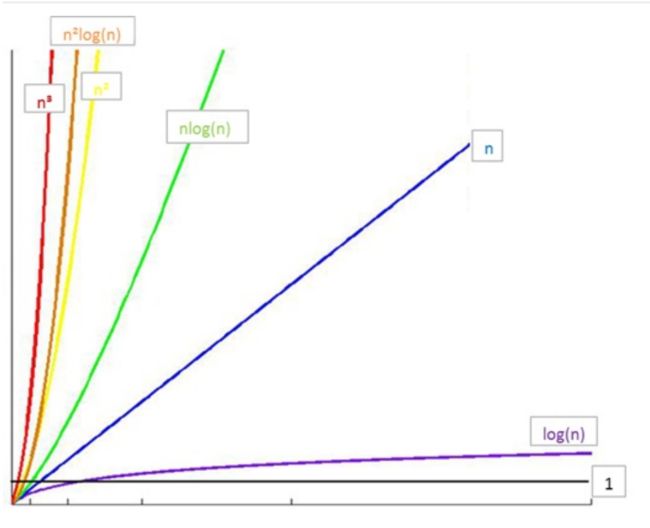
常⻅时间复杂度之间的关系
所消耗的时间从⼩到⼤
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2^n) < O(n!)
二、数据结构
2.1、数据结构基础
数据是⼀个抽象的概念,将其进⾏分类后得到程序设计语⾔中的基本类型。如:int,float,char,bool等。
数据元素之间不是独⽴的,存在特定的关系,这些关系便是结构(eg:一个人有名字和年龄,名字和年龄都属于这个人,因此数据元素不是独立的)
数据结构指数据对象中数据元素之间的关系2.2、算法和数据结构的区别
| 算法 | 数据结构 |
|---|---|
| ⾼效的程序需要在数据结构的基础上设计和选择算法 | 数据结构只是静态的描述了数据元素之间的关系 |
| 算法是为了解决实际问题⽽设计的 | 数据结构是算法需要处理的问题载体 |
综上:程序 = 数据结构 + 算法
2.3、抽象数据类型(ADT)
| 抽象数据类型 | 面向对象中的封装 |
|---|---|
| 指⼀个数学模型以及定义在此数学模型上的⼀组操作 | class包含属性和方法,属性就是存储的数据,方法就是对数据的操作 |
| 抽象数据类型就相当于面向对象中的封装,因此相当于class的概念 |
常用的数据运算:插入、删除、修改、查找、排序
2.4、基本的数据结构
2.4.1、顺序表
2.4.1.1、顺序表概念相关
将一组元素看成一个序列,用元素在序列里的位置和顺序,表示实际应用中的某种有意义的信息,或者表示数据之间的某种关系,这样的一组序列元素的组织形式,抽象的称为线性表,一个线性表是某类元素的一个集合,还记录着元素之间的一种顺序关系;
线性表两种存储形式:
- 顺序表,将元素顺序地存放在⼀块连续的存储区⾥,元素间的顺序关系由它们的存储顺序⾃然表示
- 链表,将元素存放在通过链接构造起来的⼀系列存储块中
2.4.1.2、顺序表的形式
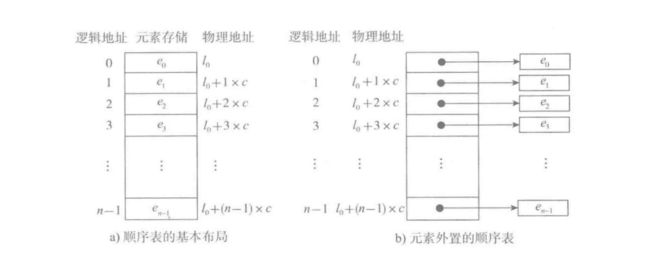
| 图a | 图b |
|---|---|
| 顺序表的基本形式,数据元素本身连续存储,每个元素所占的存储单元⼤⼩固定相同 | 如果元素的⼤⼩不统⼀,则须采⽤图b的元素外置的形式,将实际数据元素另⾏存储,⽽顺序表中各单元位置保存对应元素的地址信息(即链接) |
| 元素的下标是其逻辑地址,⽽元素存储的物理地址(实际内存地址)可以通过存储区的起始地址Loc (e )加上逻辑地址(第i个元素)与存储单元⼤⼩(c)的乘积计算⽽得,即:Loc(e ) = Loc(e ) + c* | 图b中的c不再是数据元素的⼤⼩,⽽是存储⼀个链接地址所需的存储量,这个量通常很⼩ |
**访问指定元素时⽆需从头遍历,通过计算便可获得对应地址,其时间复
杂度为O(1)**
2.4.1.3、顺序表的结构与实现
1、表中的元素集合
2、实现正确操作而需记录的信息(有关表的整体情况的信息,
这部分信息主要包括存储区的**容量**和当前表中已有的**元素个数**)
| 图a | 图b |
|---|---|
| ⼀体式结构,存储表信息的单元与元素存储区以连续的⽅式安排在⼀块存储区⾥,两部分数据的整体形成⼀个完整的顺序表对象 | 分离式结构,表对象⾥只保存与整个表有关的信息(即容量和元素个数),实际数据元素存放在另⼀个独⽴的元素存储区⾥,通过链接与基本表对象关联。 |
| ⼀体式结构整体性强,易于管理。但是由于数据元素存储区域是表对象的⼀部分,顺序表创建后,元素存储区就固定了 |
元素存储区替换
| ⼀体式结构 | 分离式结构 |
|---|---|
| 由于顺序表信息区与数据区连续存储在⼀起,所以若想更换数据区,则只能整体搬迁,即整个顺序表对象(指存储顺序表的结构信息的区域)改变了 | 若想更换数据区,只需将表信息区中的数据区链接地址更新即可,⽽该顺序表对象不变 |
元素存储区扩充
采⽤分离式结构的顺序表,若将数据区更换为存储空间更⼤的区域,则可以
在不改变表对象的前提下对其数据存储区进⾏了扩充,所有使⽤这个表的地
⽅都不必修改,这种技术实现的顺序表称为动态顺序表,因为其容量可以在使⽤中动态变化
扩充的两种策略:
| 每次扩充增加固定数⽬ | 每次扩充容量加倍 |
|---|---|
| 每次扩充增加固定数⽬的存储位置,如每次扩充增加10个元素位置,这种策略可称为线性增⻓ | 每次扩充容量加倍,如每次扩充增加⼀倍存储空间 |
| 特点:节省空间,但是扩充操作频繁,操作次数多 | 特点:减少了扩充操作的执⾏次数,但可能会浪费空间资源。以空间换时间,推荐的⽅式 |
2.4.1.4、顺序表的操作
增加元素:
a、尾端加⼊元素,时间复杂度为O(1)
b、保序的元素加⼊,时间复杂度为O(n)
删除元素:
a、删除表尾元素,时间复杂度为O(1)
b、保序的元素删除,时间复杂度为O(n)
2.4.1.5、Python中的顺序表
list和tuple两种类型采⽤了顺序表的实现技术,tuple是不可变类型,即不变的顺序表,因此不⽀持改变其内部状态的任何操作,⽽其他⽅⾯,则与list的性质类似
2.4.2、链表
1.定义
链表(Linked list)是⼀种常⻅的基础数据结构,是⼀种线性表,但是不像顺
序表⼀样连续存储数据,⽽是在每⼀个节点(数据存储单元)⾥存放下⼀个
节点的位置信息(即地址)
2.单向链表
单向链表也叫单链表,是链表中最简单的⼀种形式,它的每个节点包含两个
域,⼀个信息域(元素域)和⼀个链接域。这个链接指向链表中的下⼀个节
点,⽽最后⼀个节点的链接域则指向⼀个空值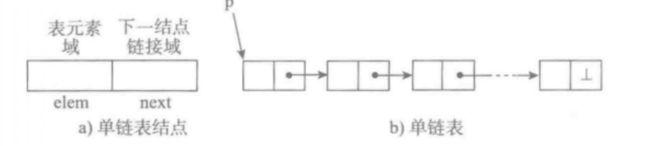
- 元素域elem⽤来存放具体的数据
- 链接域next⽤来存放下⼀个节点的位置(python中的标识)
- 变量p指向链表的头节点(⾸节点)的位置,从p出发能找到表中的任意节点
3.节点的实现与节点的操作实现
class SingleNode(object):
"""
单链表的节点实现
"""
def __int__(self, item):
self.item = item
self.next = None
class SingleLinkList(object):
"""
单链表的操作实现
"""
def __init__(self):
self.__head = None
# 判断链表为空
def is_empty(self):
return self.__head is None
# 链表长度
def length(self):
cur = self.__head
count = 0
while cur is not None:
count += 1
cur = cur.next
return count
# 遍历链表
def travel(self):
cur = self.__head
while cur is not None:
print(cur.item)
cur = cur.next
print("")
# 头部添加元素
def add(self, item):
node = SingleNode()
node.item = item
node.next = self.__head
self.__head = node
# 尾部添加元素
def append(self, item):
node = SingleNode()
node.item = item
if self.is_empty():
self.__head = node
else:
cur = self.__head
while cur.next is not None:
cur = cur.next
cur.next = node
# 指定位置添加元素
def insert(self, pos, item):
if pos <= 0:
self.add(item)
elif pos >= self.length():
self.append(item)
else:
cur = self.__head
count = 0
node = SingleNode()
node.item = item
while count < (pos - 1):
count += 1
cur = cur.next
node.next = cur.next
cur.next = node
# 删除元素
def remove(self, item):
cur = self.__head
pre = None
while cur is not None:
if cur.item == item:
if cur == self.__head:
self.__head = cur.next
else:
pre.next = cur.next
return
pre = cur
cur = cur.next
# 查找元素
def search(self, item):
cur = self.__head
while cur is not None:
if cur.item == item:
return True
cur = cur.next
return False
2.4.3、双向链表
每个节点有两个链接:⼀个指向前⼀个节点,当此节点为第⼀个节点时,指向空值;⽽另⼀个指向下⼀个节点,当此节点为最后⼀个节点时,指向空值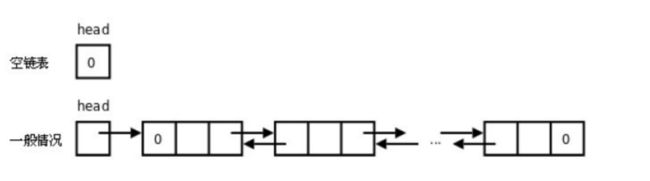
双向链表实现与操作:
class DoubleNode(object):
"""
双向链表的节点实现
"""
def __int__(self, item):
self.item = item
self.next = None
self.pre = None
class DoubleLinkList(object):
"""
双向链表的操作实现
"""
def __init__(self):
self.__head = None
# 判断链表为空
def is_empty(self):
return self.__head is None
# 链表长度
def length(self):
cur = self.__head
count = 0
while cur is not None:
count += 1
cur = cur.next
return count
# 遍历链表
def travel(self):
cur = self.__head
while cur is not None:
print(cur.item)
cur = cur.next
print("")
# 查找元素
def search(self, item):
cur = self.__head
while cur is not None:
if cur.item == item:
return True
cur = cur.next
return False
# 头部添加元素
def add(self, item):
node = DoubleNode()
node.item = item
node.next = self.__head
self.__head = node
if node.next:
node.next.pre = node
# 尾部添加元素
def append(self, item):
node = DoubleNode()
node.item = item
if self.is_empty():
self.__head = node
else:
cur = self.__head
while cur.next is not None:
cur = cur.next
node.pre = cur
cur.next = node
# 指定位置添加元素
def insert(self, pos, item):
if pos <= 0:
self.add(item)
elif pos >= self.length():
self.append(item)
else:
cur = self.__head
count = 0
node = DoubleNode()
node.item = item
while count < pos:
count += 1
cur = cur.next
node.next = cur
node.pre = cur.pre
cur.pre.next = node
cur.pre = node
# 删除元素
def remove(self, item):
cur = self.__head
while cur is not None:
if cur.item == item:
if cur == self.__head:
self.__head = cur.next
if cur.next:
self.__head.pre = None
else:
cur.pre.next = cur.next
if cur.next:
cur.next.pre = cur.pre
return
cur = cur.next2.4.4、单向循环链表
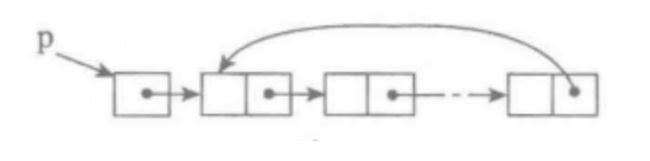
单链表的⼀个变形是单向循环链表,链表中最后⼀个节点的next域不再为
None,⽽是指向链表的头节点
单向循环链表的实习与操作实现:
class SingleNode(object):
"""
单向循环链表的节点实现
"""
def __int__(self, item):
self.item = item
self.next = None
class SingleLinkList(object):
"""
单向循环链表的操作实现
"""
def __init__(self):
self.__head = None
# 判断链表为空
def is_empty(self):
return self.__head is None
# 链表长度
def length(self):
if self.is_empty():
return 0
cur = self.__head
count = 1
while cur.next != self.__head:
count += 1
cur = cur.next
return count
# 遍历链表
def travel(self):
if self.is_empty():
print("")
return
cur = self.__head
while cur.next != self.__head:
print(cur.item)
cur = cur.next
print(cur.item)
# 头部添加元素
def add(self, item):
node = SingleNode()
node.item = item
if self.is_empty():
self.__head = node
node.next = node
cur = self.__head
while cur.next != self.__head:
cur = cur.next
node.next = self.__head
self.__head = node
cur.next = self.__head
# 尾部添加元素
def append(self, item):
node = SingleNode()
node.item = item
if self.is_empty():
self.__head = node
node.next = node
else:
cur = self.__head
while cur.next != self.__head:
cur = cur.next
cur.next = node
node.next = self.__head
# 指定位置添加元素
def insert(self, pos, item):
if pos <= 0:
self.add(item)
elif pos >= self.length():
self.append(item)
else:
cur = self.__head
count = 0
node = SingleNode()
node.item = item
while count < (pos - 1):
count += 1
cur = cur.next
node.next = cur.next
cur.next = node
# 删除元素
def remove(self, item):
if self.is_empty():
return
cur = self.__head
pre = None
while cur.next != self.__head:
if cur.item == item:
if cur == self.__head:
rear = self.__head
while rear.next != self.__head:
rear = rear.next
self.__head = cur.next
rear.next = self.__head
else:
pre.next = cur.next
return
pre = cur
cur = cur.next
if cur.item == item:
if cur == self.__head:
self.__head = None
else:
pre.next = self.__head
# 查找元素
def search(self, item):
if self.is_empty():
return False
cur = self.__head
while cur.next != self.__head:
if cur.item == item:
return True
cur = cur.next
if cur.item == item:
return True
return False2.4.5、栈
栈(stack),也称为堆栈,是⼀种容器,可存⼊数据元素、访问元素、删除元素,它的特点在于只能允许在容器的⼀端(称为栈顶端指标,英语:top)进⾏加⼊数据(英语:push)和输出数据(英语:pop)的运算。
由于栈数据结构只允许在⼀端进⾏操作,因⽽按照后进先出(LIFO, Last In First Out)的原理运作。
栈结构实现:可以⽤顺序表实现,也可以⽤链表实现
栈的操作:
class Stack(object):
def __init__(self):
self.__items = []
# 空
def is_empty(self):
return self.__items == []
# 添加元素到栈顶
def push(self, item):
self.__items.append(item)
# 取元素
def pop(self):
return self.__items.pop()
# 返回栈顶元素
def peek(self):
return self.__items[-1]
# 返回栈的长度
def size(self):
return len(self.__items)2.4.6、队列
队列(queue)是只允许在⼀端进⾏插⼊操作,⽽在另⼀端进⾏删除操作的线性表。
队列是⼀种先进先出的(First In First Out)的线性表,简称FIFO。允许插⼊
的⼀端为队尾,允许删除的⼀端为队头。队列不允许在中间部位进⾏操作!
假设队列是q=(a1,a2,……,an),那么a1就是队头元素,⽽an是队尾
元素。这样我们就可以删除时,总是从a1开始,⽽插⼊时,总是在队列最
后。这也⽐较符合我们通常⽣活中的习惯,排在第⼀个的优先出列,最后来
的当然排在队伍最后。
队列操作:
class Queue(object):
"""队列"""
def __init__(self):
self.items = []
def is_empty(self):
return self.items == []
def enqueue(self, item):
"""进队列"""
self.items.insert(0, item)
def dequeue(self):
"""出队列"""
return self.items.pop()
def size(self):
"""返回⼤⼩"""
return len(self.items)
2.4.7、双端队列
双端队列(deque,全名double-ended queue),是⼀种具有队列和栈的性质的数据结构。
双端队列中的元素可以从两端弹出,其限定插⼊和删除操作在表的两端进⾏。
双端队列可以在队列任意⼀端⼊队和出队