LeetCode 304. 二维区域和检索 - 矩阵不可变
题目描述
304. 二维区域和检索 - 矩阵不可变
解法:二维前缀和
二维前缀和矩阵中的每一个格子记录的是「以当前位置为区域的右下角(区域左上角恒定为原数组的左上角)的区域和」,那么二维前缀和矩阵就可以按照如下图所示的方法生成
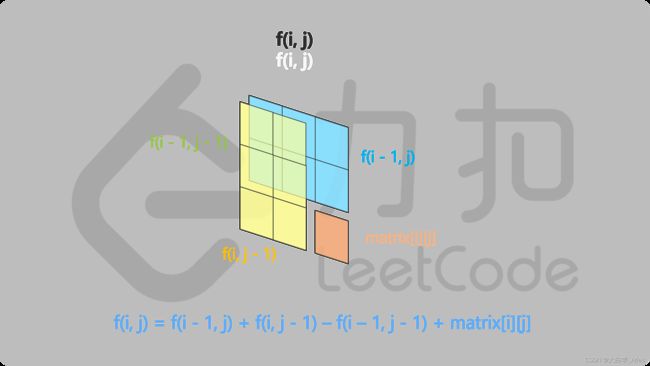
因此当我们要求 ( x 1 , y 1 ) (x1, y_1) (x1,y1) 作为左上角, ( x 2 , y 2 ) (x_2, y_2) (x2,y2) 作为右下角 的区域和的时候,可以直接利用前缀和数组快速求解:
s u m [ x 2 ] [ y 2 ] − s u m [ x 1 − 1 ] [ y 2 ] − s u m [ x 2 ] [ y 1 − 1 ] + s u m [ x 1 − 1 ] [ y 1 − 1 ] sum[x_2][y_2] - sum[x_1 - 1][y_2] - sum[x_2][y_1 - 1] + sum[x_1 - 1][y_1 - 1] sum[x2][y2]−sum[x1−1][y2]−sum[x2][y1−1]+sum[x1−1][y1−1]
class NumMatrix {
public:
vector<vector<int>> sum;
NumMatrix(vector<vector<int>>& matrix) {
int n = matrix.size();
if (n > 0)
{
int m = matrix[0].size();
sum.resize(n + 1, vector<int>(m + 1, 0));
for (int i = 1 ; i <= n; i++)
for (int j = 1; j <= m; j++)
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
row1++, row2++, col1++, col2++;
return sum[row2][col2] - sum[row1 - 1][col2] - sum[row2][col1 - 1] + sum[row1 - 1][col1 -1];
}
};
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix* obj = new NumMatrix(matrix);
* int param_1 = obj->sumRegion(row1,col1,row2,col2);
*/