数据结构:栈和队列
文章目录
- 一、栈
-
- 1.栈的概念及结构
-
- 1.栈的概念及结构
- 2.栈的实现
- 2.栈的顺序表实现
-
- 1.栈的结构体和实现的功能函数
- 2.栈的初始化,入栈和出栈操作
- 3.栈的其他操作
- 3.栈的链表实现
-
- 1.栈的结构体和实现的功能函数
- 2.栈功能函数的实现
- 二、队列
-
- 1.队列的概念及结构
-
- 1.队列的概念及结构
- 2.队列的实现
- 2.队列的顺序表实现(循环队列)
-
- 1.循环队列分析
- 2.循环队列的结构体和实现的功能函数
- 2.循环队列初始化和插入
- 2.循环队列的其他操作
- 3.队列的链表实现
-
- 1.队列的结构体和实现的功能函数
- 2.队列功能函数的实现
- 二、栈和队列应用实列:实现简单计算器
-
- 1.问题分析
- 1.代码实现
- 总结
一、栈
1.栈的概念及结构
1.栈的概念及结构
栈是一种特殊的线性表,只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端其称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出的原则。
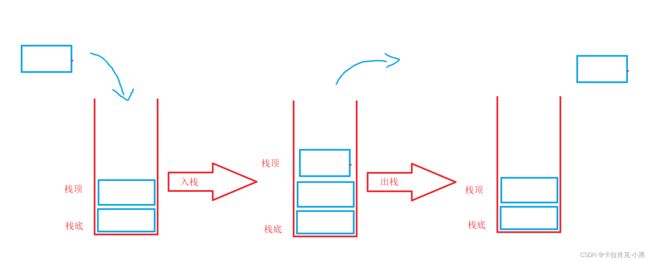
2.栈的实现
栈的实现一般可以使用数组或者链表实现
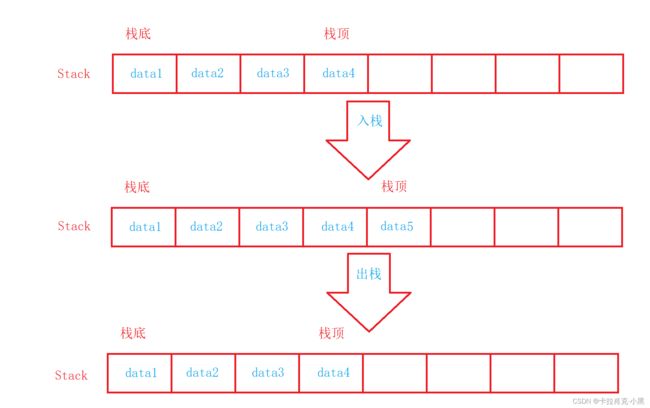
栈的数组实现:
栈的链表实现:
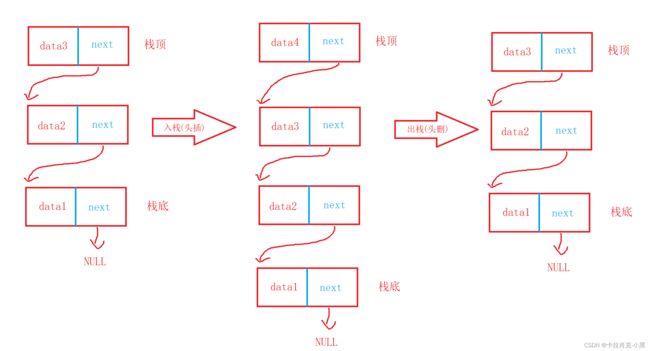
对比两种方式的插入和删除:数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。
2.栈的顺序表实现
1.栈的结构体和实现的功能函数
typedef int STDataType;
typedef struct Stack
{
STDataType* data;
int top; // 栈顶
int capacity; // 容量
}Stack;
void StackInit(Stack* ps);// 初始化栈
void StackPush(Stack* ps, STDataType data);// 入栈
void StackPop(Stack* ps);// 出栈
STDataType StackTop(Stack* ps);// 获取栈顶元素
int StackSize(Stack* ps);// 获取栈中有效元素个数
bool StackEmpty(Stack* ps);// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
void StackDestroy(Stack* ps);// 销毁栈
这里我们使用动态开辟的结构,保证栈的空间足够。数组实现我们需要一个变量来保存栈顶元素。栈顶元素也是我们栈中有效元素的个数。
2.栈的初始化,入栈和出栈操作
// 初始化
void StackInit(Stack* ps)
{
ps->top = 0;//指向栈顶的位置置为数组的起始位置
ps->capacity = 0;//把容量进行初始化
ps->data = NULL;//把数据区进行初始化
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
if (ps->top == ps->capacity)//判断空间是否已满,已满就进行扩容
{
int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;//产生新的容量
Stack* p = (Stack*)realloc(ps->data, sizeof(Stack)* newcapacity);//进行扩容
if (p == NULL)//判断是否扩容成功
{
perror("realloc");
exit(-1);
}
ps->data = p;//指向扩容后的地址
ps->capacity = newcapacity;//更新容量为新的容量
}
ps->data[(ps->top)++] = data;//把数据弹入栈顶
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
if (ps->top == 0)//判断是否还有元素
{
return;
}
ps->top--;//弹出栈顶元素
}
这里初始化,入栈和出栈操作和顺序表的操作没什么区别。
3.栈的其他操作
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
return ps->data[(ps->top) - 1];//栈顶的前一个位置为我们的栈顶元素,因为我们设置的起始位置从0开始
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->top;//栈顶元素就是栈中有效元素个数
}
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->top == 0;//返回判断结果,等于0则代表没有元素,则返回真。反之则为假。
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->data);//释放掉我们开辟的数据空间
ps->data = NULL;//把指向我们开辟数据的空间指向空
ps->top = 0;
ps->capacity = 0;
}
这里销毁注意我们的数据区的也要进行空间释放,防止造成空间泄露。
测试代码:
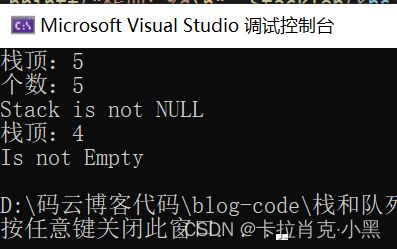
void test1()
{
Stack ps;
StackInit(&ps);
StackPush(&ps, 1);
StackPush(&ps, 2);
StackPush(&ps, 3);
StackPush(&ps, 4);
StackPush(&ps, 5);
printf("栈顶:%d\n", StackTop(&ps));// 获取栈顶元素
printf("个数:%d\n", StackSize(&ps));// 获取栈中有效元素个数
if (!StackEmpty(&ps))
{
printf("Stack is not NULL\n");
}
StackPop(&ps);
printf("栈顶:%d\n", StackTop(&ps));// 获取栈顶元素
if (!StackEmpty(&ps))
{
printf("Is not Empty\n");
}
StackDestroy(&ps);
}
int main()
{
test1();
//test2();
//test3();
//test4();
//test5();
return 0;
}
3.栈的链表实现
1.栈的结构体和实现的功能函数
typedef int STDataType;
typedef struct StackNode
{
STDataType data;
struct StackNode* next; //记录下一个区域的指针
}StackNode;
typedef struct Stack//头节点
{
int size;//记录元素的个数
StackNode head;
}Stack;
void StackInit(Stack* ps);// 初始化栈
void StackPush(Stack* ps, STDataType data);// 入栈
void StackPop(Stack* ps);// 出栈
STDataType StackTop(Stack* ps);// 获取栈顶元素
int StackSize(Stack* ps);// 获取栈中有效元素个数
bool StackEmpty(Stack* ps);// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
void StackDestroy(Stack* ps);// 销毁栈
我们这里和实现双链表一样,设置了一个特殊的头节点。头节点比正常节点多了一个变量用来记录栈中的元素个数,可以避免返回栈的元素个数时对栈进行遍历。
2.栈功能函数的实现
// 初始化栈
void StackInit(Stack* ps)
{
ps->size = 0;//初始元素为0
ps->head.next = NULL;//无元素时头节点的下一个指向空
ps->head.data = 0;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
StackNode* add = (StackNode*)malloc(sizeof(StackNode));//创建节点
if (add == NULL)//判断节点是否创建成功
{
perror("malloc");
exit(-1);
}
add->data = data;//给节点赋上数据
StackNode* pos = &(ps->head);//要取地址
add->next = pos->next;//进行头插
pos->next = add;
ps->size++;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
StackNode* pos = &(ps->head);
if (pos->next == NULL)
{
return;
}
StackNode* del = pos->next;//进行头删
pos->next = del->next;
free(del);
ps->size--;
}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
StackNode* pos = (&(ps->head))->next;
if (pos == NULL)//判断头指针的下一个是否为空
{
return;
}
return pos->data;
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->size;
}
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->size == 0;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
StackNode* pos = &(ps->head);
if (pos->next == NULL)//判断头指针的下一个是否为空
{
return;
}
StackNode* del = pos->next;
while (del != NULL)
{
pos->next = del->next;
free(del);
del = pos->next;
}
}
这里就是沿用链表的操作,注意释放节点时避免节点丢失。
测试函数:
void test2()
{
Stack ps;
StackInit(&ps);
StackPush(&ps, 1);
StackPush(&ps, 2);
StackPush(&ps, 3);
StackPush(&ps, 4);
StackPush(&ps, 5);
printf("栈顶:%d\n", StackTop(&ps));// 获取栈顶元素
printf("个数:%d\n", StackSize(&ps));// 获取栈中有效元素个数
if (!StackEmpty(&ps))
{
printf("Stack is not NULL\n");
}
StackPop(&ps);
printf("栈顶:%d\n", StackTop(&ps));// 获取栈顶元素
StackDestroy(&ps);
}
int main()
{
//test1();
test2();
//test3();
//test4();
//test5();
return 0;
}
二、队列
1.队列的概念及结构
1.队列的概念及结构
队列只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出的特点。进行插入操作的一端称为队尾 ,进行删除操作的一端称为队头。
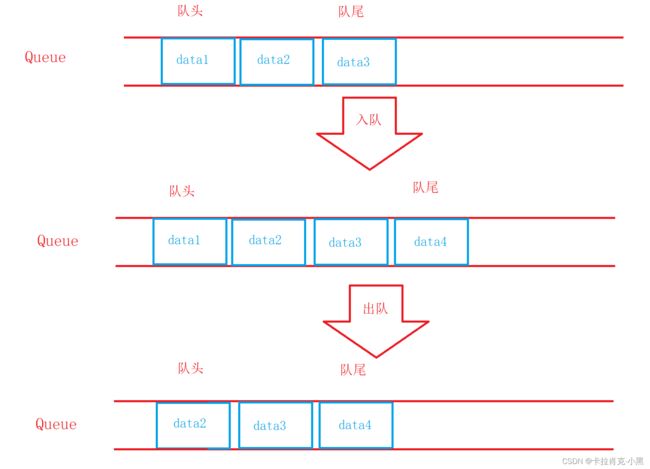
2.队列的实现
队列的实现一般可以使用数组或者链表实现
队列的链表实现:
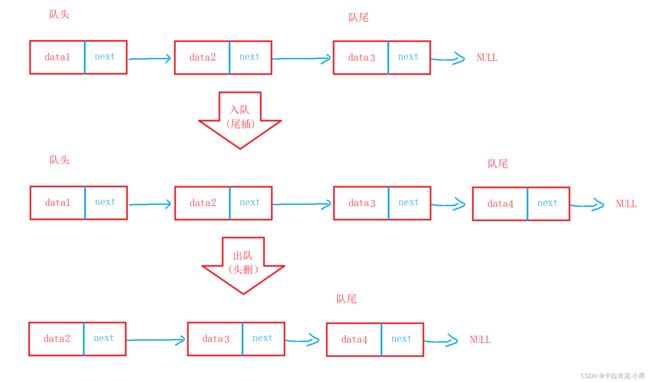
对比两种方式的插入和删除:使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,需要频繁移动数据,效率会比较低。
2.队列的顺序表实现(循环队列)
由于队列使用数组需要扩容和频繁移动数据,这样的结构并不常用,所以我们用顺序表实现循环的队列。
1.循环队列分析
我们假设数组的大小有五个元素
我们如何判断队列中的元素是否已经满了呢?
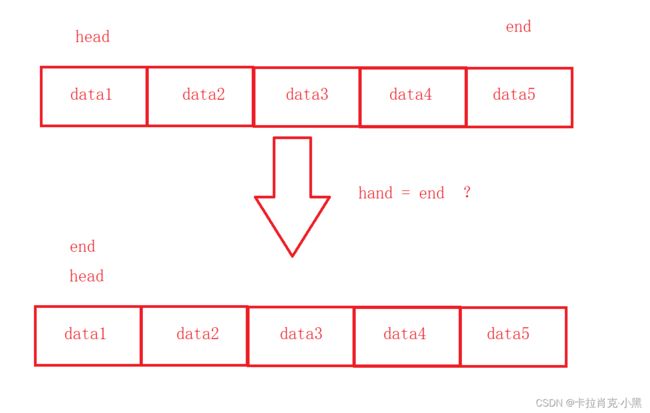
用头位置等于尾位置吗?
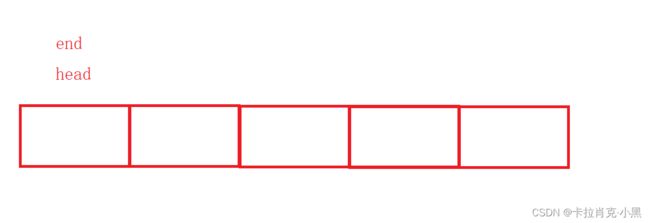
上述一个元素也没有会不会直接判断为数组已满呢?
我们的解决办法是保证一个位置为空,当尾位置等于头位置时即为队列满,即队尾不存储数据。
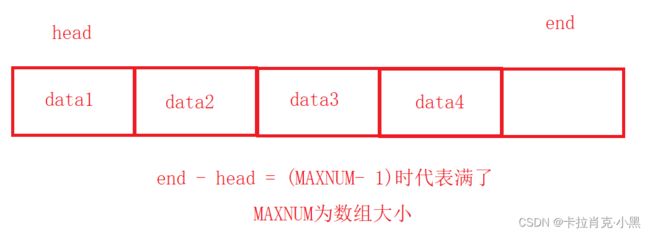
2.循环队列的结构体和实现的功能函数
#define MAXNUM 5
typedef int QDataType;
typedef struct QListNode
{
QDataType data[5];
int head;//对头元素
int end;//队尾元素
}QNode;
void QueueInit(QNode* q);// 初始化队列
void QueuePush(QNode* q, QDataType data);// 队尾入队列
void QueuePop(QNode* q);// 队头出队列
QDataType QueueFront(QNode* q);// 获取队列头部元素
QDataType QueueBack(QNode* q);// 获取队列队尾元素
int QueueSize(QNode* q);// 获取队列中有效元素个数
int QueueEmpty(QNode* q);// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
void QueueDestroy(QNode* q);// 销毁队列
2.循环队列初始化和插入
// 初始化队列
void QueueInit(QNode* q)
{
q->head = 0;
q->end = 0;
}
// 队尾入队列
void QueuePush(QNode* q, QDataType data)
{
assert(q);
if ((q->end - q->head) == (MAXNUM-1))//尾元素和首元素相差最大数量减一个元素代表队列已满
{
printf("队列已满,无法插入\n");
return;
}
q->data[(q->end) % MAXNUM] = data;
q->end++;
}
我们对队列进行插入时要对队尾元素进行取模运算。防止插入时造成越界。
2.循环队列的其他操作
// 队头出队列
void QueuePop(QNode* q)
{
assert(q);
if (q->head == q->end)//尾元素和首元素相同证明队列中没有元素
{
printf("没有元素可以出队\n");
return;
}
q->head++;
}
// 获取队列头部元素
QDataType QueueFront(QNode* q)
{
assert(q);
if (q->head == q->end && q->end != 0)//尾元素和首元素相同证明队列中没有元素
{
printf("没有元素可以查看\n");
return -1;
}
return q->data[(q->head) % MAXNUM];
}
// 获取队列队尾元素
QDataType QueueBack(QNode* q)
{
assert(q);
if (q->head == q->end && q->end != 0)//尾元素和首元素相同证明队列中没有元素
{
printf("没有元素可以查看\n");
return -1;
}
return q->data[(q->end - 1) % MAXNUM];
}
// 获取队列中有效元素个数
int QueueSize(QNode* q)
{
assert(q);
return q->end - q->head;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(QNode* q)
{
assert(q);
return q->head == q->end;
}
// 销毁队列
void QueueDestroy(QNode* q)
{
assert(q);
q->head = 0;
q->end = 0;
}
我们返回队头队尾数据要看尾是否在0位置,为0代表一个元素还没插入。我们进行插入返回元素的操作都需要进行取模操作!!!
测试函数:
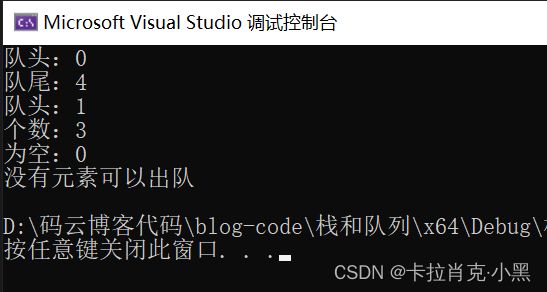
void test3()
{
QNode qu;
QueueInit(&qu);
int i = 0;
for(i = 0; i < 5; i++)
{
QueuePush(&qu, i);
}
printf("队头:%d\n", QueueFront(&qu));
printf("队尾:%d\n", QueueBack(&qu));
QueuePop(&qu);
printf("队头:%d\n", QueueFront(&qu));
printf("个数:%d\n", QueueSize(&qu));
printf("为空:%d\n", QueueEmpty(&qu));
QueuePop(&qu);
QueuePop(&qu);
QueuePop(&qu);
QueuePop(&qu);
QueueDestroy(&qu);
}
int main()
{
//test1();
//test2();
test3();
//test4();
//test5();
return 0;
}
3.队列的链表实现
1.队列的结构体和实现的功能函数
typedef int QDataType;
typedef struct QListNode
{
QDataType data;
struct QListNode* next;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* head;
QNode* end;
}Queue;
void QueueInit(Queue* q);// 初始化队列
void QueuePush(Queue* q, QDataType data);// 队尾入队列
void QueuePop(Queue* q);// 队头出队列
QDataType QueueFront(Queue* q);// 获取队列头部元素
QDataType QueueBack(Queue* q);// 获取队列队尾元素
int QueueSize(Queue* q);// 获取队列中有效元素个数
int QueueEmpty(Queue* q);// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
void QueueDestroy(Queue* q);// 销毁队列
我们设置了一个结构体用来存储头节点和尾节点,目的是为了减少遍历。
2.队列功能函数的实现
//初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->head = NULL;
q->end = NULL;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* pos = (QNode*)malloc(sizeof(QNode));
if (pos == NULL)
{
perror("malloc");
exit(-1);
}
pos->data = data;
pos->next = NULL;
if (q->end == NULL)
{
q->head = pos;
q->end = pos;
}
else
{
q->end->next = pos;
q->end = q->end->next;
}
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
QNode* del = q->head;
if (q->head == q->end && q->end != NULL)//当头指针等于尾指针时证明队列中没有元素
{
printf("没有元素可以出队\n");
return;
}
q->head = q->head->next;
free(del);
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
if (q->head == q->end && q->end != NULL)//当头指针等于尾指针时证明队列中没有元素
{
printf("没有元素可以查看\n");
return -1;
}
return q->head->data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
if (q->head == q->end && q->end != NULL)//当头指针等于尾指针时证明队列中没有元素
{
printf("没有元素可以查看\n");
return -1;
}
return q->end->data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
int size = 0;
QNode* pos = q->head;
while (pos != q->end)
{
size++;
pos = pos->next;
}
return size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
assert(q);
return q->head == q->end;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* del = q->head;
while (del != q->end)
{
q->head = del->next;
free(del);
del = q->head;
}
free(q->head);
q->head = NULL;
q->end = NULL;
}
测试函数:
void test4()
{
Queue qu;
QueueInit(&qu);
int i = 0;
for(i = 0; i < 5; i++)
{
QueuePush(&qu, i);
}
printf("队头:%d\n", QueueFront(&qu));
printf("队尾:%d\n", QueueBack(&qu));
QueuePop(&qu);
printf("队头:%d\n", QueueFront(&qu));
printf("个数:%d\n", QueueSize(&qu));
printf("为空:%d\n", QueueEmpty(&qu));
QueuePop(&qu);
QueuePop(&qu);
QueuePop(&qu);
QueuePop(&qu);
QueueDestroy(&qu);
}
int main()
{
//test1();
//test2();
//test3();
test4();
//test5();
return 0;
}
二、栈和队列应用实列:实现简单计算器
计算10+(10+20*30)*4-50
1.问题分析
我们计算需要进行优先级比较,是否含有括号,数据的存储等,我们需要两个栈来进行存储,一个符号栈,一个数字栈。
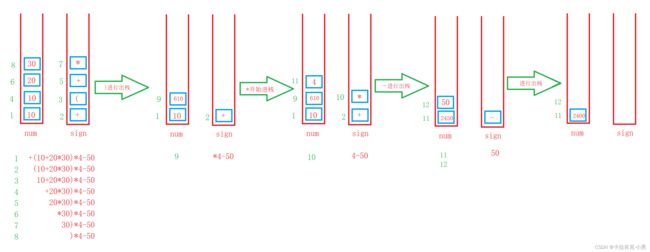
思路分析:
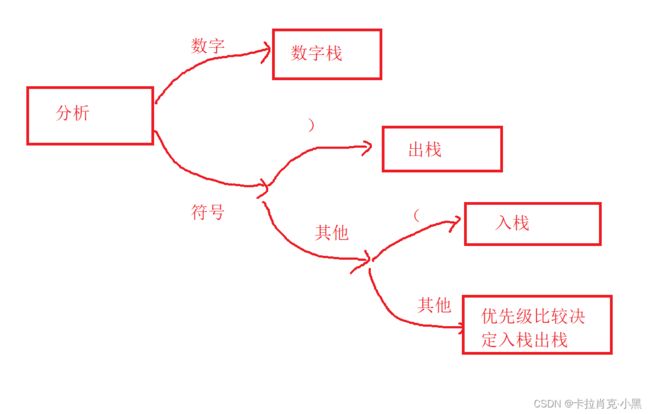
1.代码实现
void Count(Stack* num, int headsign)
{
int n1 = 0;//用于计算的变量1
int n2 = 0;//用于计算的变量2
//已经是指针了,不可以在取地址了
n2 = StackTop(num);//n2先进性出栈
StackPop(num);//数字出栈
n1 = StackTop(num);//n2出栈是为了防止除法是顺序错乱
StackPop(num);//数字出栈
int sum = 0;//用来存储两个值的结果
switch (headsign)//判断符号
{
case '+':
sum = n1 + n2;
break;
case '-':
sum = n1 - n2;
break;
case '*':
sum = n1 * n2;
break;
case '/':
sum = n1 / n2;
break;
default:
exit(-1);//未知符号,程序退出
}
//入数字栈
StackPush(num, sum);
}
void Match_Brace(Stack* sign, Stack* num)//开始匹配左括号
{
int headsign = 0;//存储栈顶的元素符号
headsign = StackTop(sign);//获取栈顶元素符号
while(!StackEmpty(sign))//符号栈不为空则一直进行循环, 直到在左括号处结束
{
if (headsign == '(')//如果为左括号则直接出栈结束
{
StackPop(sign);//符号出栈
break;
}
else
{
//计算
Count(num, headsign);//计算函数
StackPop(sign);//符号出栈
}
headsign = StackTop(sign);//获取栈顶元素符号
}
}
int Priority(int symbol)
{
switch (symbol)//判断符号
{
case '(':
return 0;
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
default:
exit(-1);//未知符号,程序退出
}
}
void Match_Symbols(Stack* sign, Stack* num, int symbol)
{
if (StackEmpty(sign) || symbol == '(')//如果栈为空或者为左括号,则直接入栈
{
StackPush(sign, symbol);//入栈
return;
}
int headsign = 0;//存储栈顶的元素符号
headsign = StackTop(sign);//获取栈顶元素符号
if (Priority(symbol) > Priority(headsign))//优先级比较,该符号优先级高则直接入栈
{
StackPush(sign, symbol);//入栈
return;
}
while(Priority(symbol) <= Priority(headsign))//直到优先级高于栈顶元素,停止循环
{
//计算
Count(num, headsign);//计算函数
StackPop(sign);//栈顶符号出栈
if (StackEmpty(sign))//栈为空则退出循环
{
break;
}
headsign = StackTop(sign);//获取栈顶元素符号
}
StackPush(sign, symbol);//入栈
}
void test5()
{
Stack num;//存储数字所使用的栈
Stack sign;//存储算数符号所用的栈
StackInit(&num);//对数字栈进行初始化
StackInit(&sign);//对符号栈进行初始化
char* s = "10+(10+20*30)*4-50";//要计算的表达式
int i = 0;//用来判断表达式是否已到结尾
int sum = 0;//用来存储一个整形数据
int flag = 0;//用来判断是否取完一个整形元素
while (s[i] != '\0')
{
if (isdigit(s[i]))//判断是否为数字
{
sum = sum * 10 + (s[i] - '0');//更新sum的值
flag = 1;//把标志位置为1,为后面判断是否入栈准备
}
else
{
if (flag == 1)//判断该数字是否以入栈
{
//入数字栈
StackPush(&num, sum);
flag = 0;//更新标志位
sum = 0;//更新sum值,防止下次计算时出错
}
if (s[i] == ')')//开始匹配左括号
{
//进行出栈匹配左括号
Match_Brace(&sign, &num);
}
else//字符为( + - * /
{
//进行优先级比较
Match_Symbols(&sign, &num,s[i]);
}
}
i++;
}
if (flag == 1)//判断该数字是否以入栈
{
//入数字栈
StackPush(&num, sum);
flag = 0;//更新标志位
sum = 0;//更新sum值,防止下次计算时出错
}
int headsign = 0;//存储栈顶的元素符号
while (!StackEmpty(&sign))//符号栈不为空则一直进行计算
{
headsign = StackTop(&sign);//获取栈顶元素符号
//计算
Count(&num, headsign);
StackPop(&sign);//符号出栈
}
printf("%d\n", StackTop(&num));
StackDestroy(&num);//销毁数字栈
StackDestroy(&sign);//销毁字符栈
}
int main()
{
//test1();
//test2();
//test3();
//test4();
test5();
return 0;
}
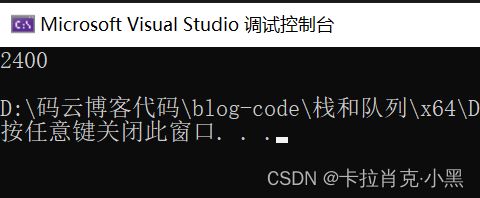
注意函数对指针的二次传参不需要在进行取地址,在计算机中计算机识别的是字符,所以我们需要一个字符一个字符的进行,这时间需要我们判断这个数字到底几位数,需要我们一个临时量,也可以用库函数atoi实现。其他按照思路可以轻而易举的实现。
总结
栈和队列都是含有限制的线性表。前面的知识扎实的话实现栈和队列没有一点问题。都是顺序表和链表的其中一部分。