HDU 2481 Toy(Burnside引理)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2481
题意:外面有一圈N个结点,中心有一个结点与N个结点都相连,总共就是2*N条边,删除N条边,使N+1个点连通,旋转相同视为等价,问有多少种情况。
思路:源地址:http://blog.csdn.net/acm_cxlove/article/details/7868589 首先计算外圈有n个点有多少种可能,然后再考虑旋转。这里任意取两个结点a、b讨论。那么总数便是a,b断开的种数与a,b连在一起的种数的和(这种分析方法很重要)。f(n)表示外圈有n个结点时,而a,b是断开的种数;g(n)表示外圈有n个结点时,而a,b是连在一起的种数。
(1)如果a,b之间是断开的(如下面左侧的图),如果与a直接相连的为k个(加上a自己),那么显然这k个要与其它的保持连通的,与中心必须有一条边,如果有多条边就形成环了,显然不满足生成树。另外n-k为f[n-k]种,因为这n-k种肯定是断开的。枚举k,则f[n]=sigma(k*f[n-k])(1<=k<=n)。
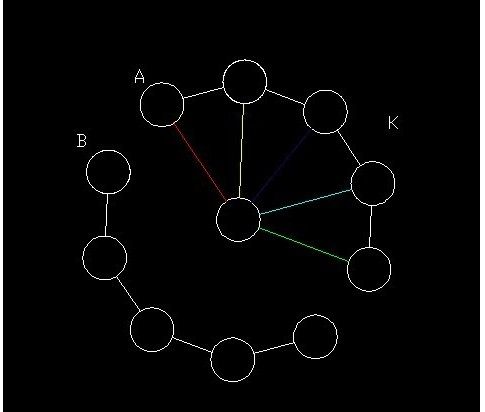
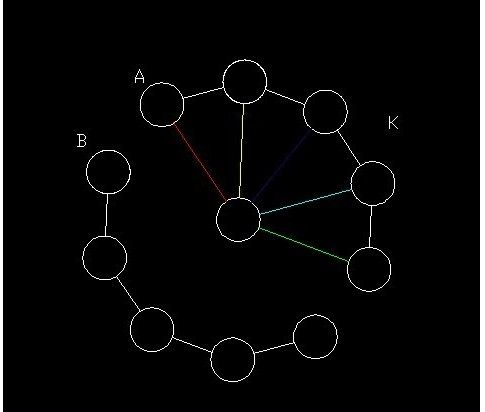
(2)如果a,b是连在一起的(如上面右侧的图),如果与a,b相连的为k个(包括a,b),那么a,b是相邻的在这k个位置选择就有k-1种,而这k个与中心相连的选择有k种,剩下的与这部分是分开的,则为f[n-k],所以可以枚举k,最终结果g[n]=sigma((k-1)*k*f[n-k])(2<=k<=n)。
最终的种数便是T[n]=f[n]+g[n]。
由f[n]=sigma(k*f[n-k])(1<=k<=n)得到:
f[n]=1*f(n-1)+2*f(n-2)+3*f(n-3)+……+(n-1)*f(1)+n*f[0]
=s[n-1]+1*f(n-2)+2*f(n-3)+……+(n-2)*f(1)+(n-1)*f[0]
=s[n-1]+f[n-1]
=s[n-2]+f[n-1]+f[n-1]
=s[n-2]+2*f[n-1]
=f[n-1]-f[n-2]+2*f[n-1]
=3*f[n-1]-f[n-2] 其中f[0]=1,f[1]=1,f[2]=3,f[3]=8
g[n] =sigama((k-1)*k*f[n-k]) (2<=k<=n) 从这里可以得到g[1]=0
=1*2*f[n-2]+2*3*f[n-3]+3*4*f[n-4]+……+(n-1)*(n-2)*f[1]+n*(n-1)*f[0]
g[n-1]= 1*2*f[n-3]+2*3*f[n-4]+……+(n-2)*(n-3)*f[1]+(n-1)*(n-2)*f[0]
所以:g(n)-g(n-1)=2*f[n-2]+4*f[n-3]……(2*(n-2))*f[1]+2*(n-1)*f[0]
=2*(1*f[n-2]+2*f[n-3]+……+(n-2)*f[1]+(n-1)*f[0])
=2*f[n-1]
进而得到:g[n]=2*(f[1]+f[2]+f[3]……f[n-1])+g[1]=2*(s[n-1]-f[0])+g[1]
=2*(f[n]-f[n-1]-1)+g[1]
=2*(f[n]-f[n-1]-1) 其中f[0]=1,g[1]=0
对于f[n]的求法,可以用矩阵快速幂乘解决:定义矩阵A

则(f[n],f[n-1])=(f[1],f[0])*A^(n-1)。而g[n]也就可以顺便得到,T[n]就处理完毕了。
然后就是Burnside定理,同样N比较大,肯定是要用欧拉函数优化,枚举循环个数。n对MOD是可能没有逆元的,用(a/b)%c=(a%(b*c))/b。这样的话把取模就变成了MOD*N,范围到了10^18,这样子的话中间的乘法便会溢出64位整数。乘法二分。
const int N=2;
const int M=40000;
int n;
i64 mod;
class Matrix
{
public:
i64 a[N][N];
Matrix()
{
clr(a,0);
}
void init(int x)
{
if(x==0) a[0][0]=a[0][1]=a[1][0]=a[1][1]=0;
else if(x==1) a[0][0]=a[1][1]=1,a[0][1]=a[1][0]=0;
}
};
i64 mul(i64 a,i64 b)
{
a=(a%mod+mod)%mod;
b=(b%mod+mod)%mod;
i64 ans=0;
while(b)
{
if(b&1) ans=(ans+a)%mod;
a=(a+a)%mod;
b>>=1;
}
return ans;
}
Matrix operator*(Matrix &a,Matrix &b)
{
int i,j,k;
Matrix p;
p.init(0);
FOR0(i,2) FOR0(j,2) FOR0(k,2)
{
(p.a[i][j]+=mul(a.a[i][k],b.a[k][j])%mod)%=mod;
}
return p;
}
Matrix operator^(Matrix a,int t)
{
Matrix ans;
ans.init(1);
while(t)
{
if(t&1) ans=ans*a;
a=a*a;
t>>=1;
}
return ans;
}
Matrix a,b;
int prime[M],tag[M],cnt;
vector<int> factor;
void init()
{
int i,j;
for(i=2;i<180;i++) if(!tag[i])
{
for(j=i*i;j<M;j+=i) tag[j]=1;
}
for(i=2;i<M;i++) if(!tag[i])
{
prime[++cnt]=i;
}
}
int eular(int n)
{
int ans=n,i;
for(i=1;i<=cnt&&(i64)prime[i]*prime[i]<=n;i++) if(n%prime[i]==0)
{
ans=ans/prime[i]*(prime[i]-1);
while(n%prime[i]==0) n/=prime[i];
}
if(n>1) ans=ans/n*(n-1);
return ans;
}
i64 get(int n)
{
if(n==1) return 1;
if(n==2) return 5;
a=b^(n-2);
i64 f=3*a.a[0][0]+a.a[1][0];
i64 g=2*(f-(3*a.a[0][1]+a.a[1][1])-1);
return (g+f)%mod;
}
int main()
{
init();
b.a[0][0]=3; b.a[0][1]=1; b.a[1][0]=-1; b.a[1][1]=0;
while(scanf("%d%I64d",&n,&mod)!=-1)
{
mod*=n;
i64 ans=0;
int i;
for(i=1;i*i<=n;i++) if(n%i==0)
{
(ans+=mul(eular(i),get(n/i))%mod)%=mod;
if(i*i==n) continue;
(ans+=mul(eular(n/i),get(i))%mod)%=mod;
}
ans=ans/n%(mod/n);
printf("%I64d\n",ans);
}
return 0;
}