无重复字符串的排列组合

面试题 08.07. 无重复字符串的排列组合

无重复字符串的排列组合。编写一种方法，计算某字符串的所有排列组合，字符串每个字符均不相同。

示例1:

 输入：S = "qwe"
 输出：["qwe", "qew", "wqe", "weq", "ewq", "eqw"]

示例2:

 输入：S = "ab"
 输出：["ab", "ba"]

提示:

1. 字符都是英文字母。
2. 字符串长度在[1, 9]之间

个人所写

这里看不懂就不要看了,==>写的太麻烦,时间一久我也看不懂;

class Solution {
public:
    vector permutation(string S) {
vectorans;
int temp[S.size()];
memset(temp,0,sizeof temp);
find(ans,"",S.size(), S,temp);
return ans;
    }
   void  find(vector&ans,string s,int n,string all,int temp[])//函数参数有点多;
    {
        if(n==0)
        {
            ans.push_back(s);return ;
        }
         for(int i=0;i

这是第一次凭自己的本事做出来的这种递归题,所以想记录下来.当然代码有些麻烦.

---

方法技巧

还有一个专门的函数:next_permutation()

按照STL文档的描述，next_permutation函数将按字母表顺序生成给定序列的下一个较大的排列，直到整个序列为降序为止。prev_permutation函数与之相反，是生成给定序列的上一个较小的排列。

这是一个求一个排序的下一个排列的函数，可以遍历全排列,要包含头文件

有上述可知,对于next_permutation而言,必须先进行从小到大的排序,否则只要数组不是从小到大,那么就得出的结果一定不是正确的答案

看代码:

int a[];
sort(a,a+n);//此处是一定需要的,如上述的描述;如果不进行排序,那么结果就是:从数组中当前的字典序开始依次增大直至到最大字典序。
do
{
}
while(next_permutation(a,a+n));
//这是一个标准的模板;

如果直接用while(next_permutation(a,a+n)){},

因为在一开始判断的时候,就已经生成了一个a的全序列,所以少的那一个就是字典序最小的那一个;

//如果按字母表顺序还含有比较大的排序,那么next_permutation()就会返回true;

一种比较简洁的方法

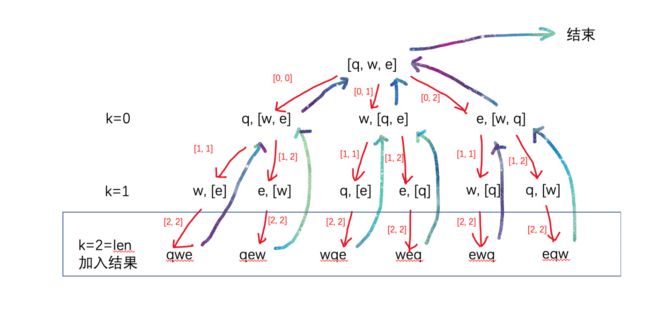
class Solution {
private:
    vector res;
    void dfs(string &s, int left){
        if(left==s.size()) res.emplace_back(s);
        for(int i=left; i permutation(string S) {
        res.clear();
        dfs(S, 0);
        return res;
    }
};

这道题也同样说明,对于一个dfs的题目,大可以不必死板的用visited数组来表示是否被访问,还可以用swap等其他的方法