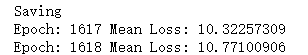【项目实践】基于LSTM的一维数据扩展与预测

基于LSTM的一维数据拟合扩展

一、引(fei)言(hua)

我在做Sri Lanka生态系统服务价值计算时，中间遇到了一点小问题。从世界粮农组织(FAO)上获得Sri Lanka主要农作物产量和价格数据时，其中的主要作物Sorghum仅有2001-2006年的数据，而Millet只有2001-2005,2020-2021这样的间断数据。虽然说可以直接剔除这种过分缺失的数据，但这无疑会对生态因子的计算造成重大影响。所以我想要不要整个函数把他拟合一下，刚好Maize和Rice有2001-2021的完备数据，于是，这个文档就这样诞生了。

---

二、数据

数据来自FAO，考虑到可能有同学想要跟着尝试一下，这里给出用到的数据。

作物产量

作物价格

2.1 数据探查

我们读取数据，并进行简单的统计量查看。如果要进一步深入研究数据分布及可视化，可以看看我的这篇文章

import pandas as pd

path=r"YourPath"

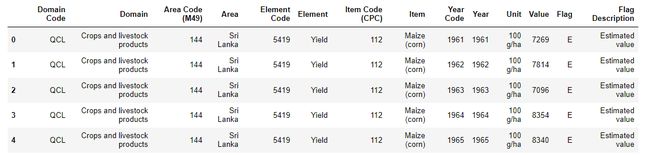
yield_=pd.read_csv(path+r"\yield.csv")
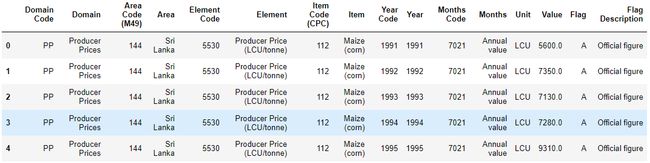
pp_=pd.read_csv(path+r"\Producer Prices.csv")

yield_.head()

需要用到的属性只有Item,Year,Unit,Value

所以我们做这样的处理：

yield_=yield_[["Item","Year","Unit","Value"]]

可以看到有些数据是从1961年开始的，太旧了就不用了，我们从2001年开始。

yield_=yield_[yield_["Year"]>2000]

同样，我们来看看pp_的情况：

pp_.head()

pp_=pp_[["Item","Year","Value","Element"]]
pp_=pp_[pp_["Year"]>2000]

实际上，在这个数据里，产量已经没有问题了。我们只需要做一个简单的处理：

yield_.groupby("Item").mean()["Value"]/10 #转为千克

便可拿到每种作物近二十年的平均产量。

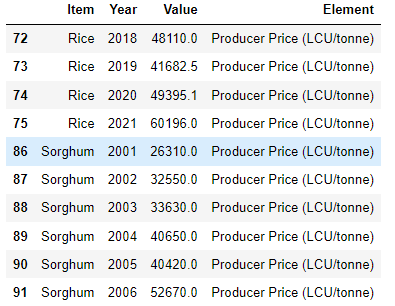
好了现在大问题出现在价值上，我们从下往上看就知道了：

pp_.tail(10)

高粱只有2006年的，那有没有办法利用现成的数据将其扩展呢？

实际上，这类拟合问题有很多种解决方案，但是本问题涉及到时间，之前时间段的因子，以及可能的周期性，都会增加拟合的复杂性。所以，在这里我们采用LSTM来填充数据。

---

三、模型构建

在本小节，我们将比较传统一维CNN与RNN在结果上的异同。

一般做一维RNN时，可以指定一个时间窗口，比如用2006,2007,2008年的数据，推理2009年的数据，用2007,2008,2009年推理2010年。

我们现在要用之前处理好的pp_c数据中的玉米产量，来预测高粱产量。所以第一步就是将其转化为torch接受的格式。

别忘记导入模块：

import torch
import torch.nn as nn
from torch.nn import functional as F

x=pp_c[pp_c['Item']=="Maize (corn)"]['Value']
x=torch.FloatTensor(x)

之前写数据迭代器的时候，除了可以继承自torch.utils.data.DataLoader，也可以是任意的可迭代对象。这里我们可以简单的设置一个类：

# 设置迭代器
class MyDataSet(object):
    def __init__(self,seq,ws=6):
        # ws是滑动窗口大小
        self.ori=[i for i in seq[:ws]]
        self.label=[i for i in seq[ws:]]
        self.reset()
        self.ws=ws

    def set(self,dpi):
        # 添加数据
        self.x.append(dpi)
        
    def reset(self):
        # 初始化
        self.x=self.ori[:]
        
    def get(self,idx):
        return self.x[idx:idx+self.ws],self.label[idx]
    
    def __len__(self):
        return len(self.x)

哦这边提一下，有两种方式，一种是用原始数据做预测，一种是用预测数据做预测，可能有点抽象，下面举个例子。

假设$A=[a1,a2,a3,a4,a5,a6]$，时间窗口大小为3。

用原始数据做预测，那么输入值为：$a1,a2,a3$，得到的结果将与$a4$做比较。下一轮输入为$a2,a3,a4$，得到的结果将与$a5$做比较。

而用预测的数据做预测，第一轮输入值为$a1,a2,a3$，得到的结果是$b4$，在与$a4$做比较后，下一轮的输入为$a2,a3,b4$，会出现如下情况：

输入数据为$b4,b5,b6$。

我们现在举的例子是用预测的数据做预测。当然，最后也会给出一个用原始数据做预测的版本，那个版本相对简单。

ws=6 # 全局时间窗口
train_data=MyDataSet(x,ws)

---

网络的架构如下：

   
class Net3(nn.Module):
    def __init__(self,in_features=54,n_hidden1=128,n_hidden2=256,n_hidden3=512,out_features=7):
        super(Net3, self).__init__()
        self.flatten=nn.Flatten()
        self.hidden1=nn.Sequential(
            nn.Linear(in_features,n_hidden1,False),
           
            nn.ReLU()
        )
        self.hidden2=nn.Sequential(
            nn.Linear(n_hidden1,n_hidden2),

            nn.ReLU()
        )
        self.hidden3=nn.Sequential(
            nn.Linear(n_hidden2,n_hidden3),

            nn.ReLU()
        )
        self.out=nn.Sequential(nn.Linear(n_hidden3,out_features))

    def forward(self,x):
        x=self.flatten(x)
        x=self.hidden2(self.hidden1(x))
        x=self.hidden3(x)
        return self.out(x)



class CNN(nn.Module):
    def __init__(self, output_dim=1,ws=6):
        super(CNN, self).__init__()
        self.relu = nn.ReLU(inplace=True)
        self.conv1 = nn.Conv1d(ws, 64, 1)
        self.lr = nn.LeakyReLU(inplace=True)
        self.conv2 = nn.Conv1d(64, 128, 1)

        self.bn1, self.bn2 = nn.BatchNorm1d(64), nn.BatchNorm1d(128)
        self.bn3, self.bn4 = nn.BatchNorm1d(1024), nn.BatchNorm1d(128)
        self.flatten = nn.Flatten()
        self.lstm1 = nn.LSTM(128, 1024)
        self.lstm2 = nn.LSTM(1024, 256)
        self.lstm3=nn.LSTM(256,512)
        self.fc = nn.Linear(512, 512)
        self.fc4=nn.Linear(512,256)
        self.fc1 = nn.Linear(256, 64)
        self.fc3 = nn.Linear(64, output_dim)

    @staticmethod
    def reS(x):
        return x.reshape(-1, x.shape[-1], x.shape[-2])

    def forward(self, x):
        x = self.reS(x)
        x = self.conv1(x) 
        x = self.lr(x)

        x = self.conv2(x) 
        x = self.lr(x)

        x = self.flatten(x)

        # LSTM部分
        x, h = self.lstm1(x)
        x, h = self.lstm2(x)
        x,h=self.lstm3(x)
        x, _ = h

        x = self.fc(x.reshape(-1, ))
        x = self.relu(x)
        x = self.fc4(x)
        x = self.relu(x)
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc3(x)

        return x

Net3主要是一维卷积，CNN加入了LSTM结构。至于名字，是随便取的…跟内容并无关系。

---

def Train(model,train_data,seed=1):
    device="cuda" if torch.cuda.is_available() else "cpu"
    model=model.to(device)
    Mloss=100000
    path=r"YourPath\%s.pth"%seed
    # 设置损失函数,这里使用的是均方误差损失
    criterion = nn.MSELoss()
    # 设置优化函数和学习率lr
    optimizer=torch.optim.Adam(model.parameters(),lr=1e-5,betas=(0.9,0.99),
                               eps=1e-07,weight_decay=0)
    # 设置训练周期
    epochs =3000
    criterion=criterion.to(device)
    model.train()
    for epoch in range(epochs):
        total_loss=0

        for i in range(len(x)-ws):
            # 每次更新参数前都梯度归零和初始化
            seq,y_train=train_data.get(i) # 从我们的数据集中拿出数据
            seq,y_train=torch.FloatTensor(seq),torch.FloatTensor([y_train])
            seq=seq.unsqueeze(dim=0)
            seq,y_train=seq.to(device),y_train.to(device)

            optimizer.zero_grad()
            # 注意这里要对样本进行reshape，
            # 转换成conv1d的input size（batch size, channel, series length）
            y_pred = model(seq)
            loss = criterion(y_pred, y_train)
            loss.backward()
            train_data.set(y_pred.to("cpu").item()) # 再放入预测数据
            optimizer.step()
            total_loss+=loss

        train_data.reset()
        if total_loss.tolist()<Mloss:
            Mloss=total_loss.tolist()
            torch.save(model.state_dict(),path)
            print("Saving")
        print(f'Epoch: {epoch+1:2} Mean Loss: {total_loss.tolist()/len(train_data):10.8f}')
    return model

正常训练就OK

d=CNN(ws=ws)
Train(d,train_data,4)

平均损失在10点左右，还有很大优化空间。当然我们这里只是举个非常简单的例子，就是个baseline

checkpoint=torch.load(r"YourPath\4.pth")
d.load_state_dict(checkpoint) # 加载最佳参数
d.to("cpu")

---

四、结果可视化

我们这里用到Pyechart进行可视化。

from pyecharts.charts import *
from pyecharts import options as opts
from pyecharts.globals import CurrentConfig

pre,ppre=[i.item() for i in x[:ws]],[]
# pre 是用原始数据做预测
# ppre 用预测数据做预测
for i in range(len(x)-ws+1):
    ppre.append(d(torch.FloatTensor(x[i:i+ws]).unsqueeze(dim=0)))
    pre.append(d(torch.FloatTensor(pre[-ws:]).unsqueeze(dim=0)).item())

l=Line()
l.add_xaxis([i for i in range(len(x))])
l.add_yaxis("Original Data",x.tolist())
l.add_yaxis("Pred Data(Using Raw Datas)",x[:ws].tolist()+[i.item() for i in ppre])
l.add_yaxis("Pred Data(Using Pred Datas)",pre)
l.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
l.set_global_opts(title_opts=opts.TitleOpts(title='LSTM CNN'))

l.render_notebook()

根据时间窗口的不同，可以得到不同的结果。

ws=4

ws=5

ws=6

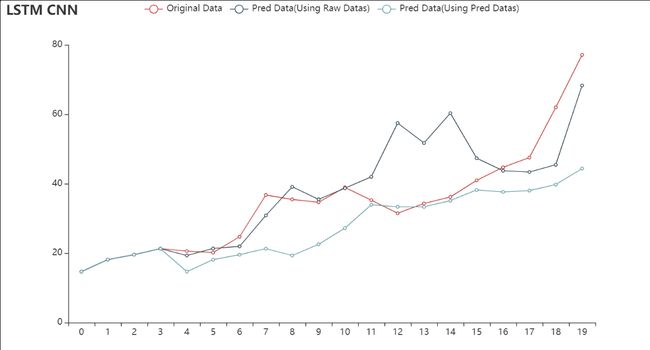
从结果上来看，时间窗口越大越好。但是这里我们只能到六了，再大就不礼貌了。(高粱只有六个节点的数据)。

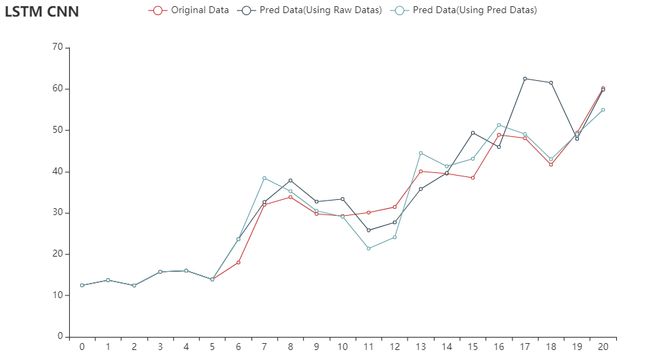
至于验证，我们可以选Rice做验证：

x=torch.FloatTensor(pp_c[pp_c['Item']=="Rice"]['Value'].tolist())
pre,ppre=[i.item() for i in x[:ws]],[]
for i in range(len(x)-ws+1):
    ppre.append(d(torch.FloatTensor(x[i:i+ws]).unsqueeze(dim=0)))
    pre.append(d(torch.FloatTensor(pre[-ws:]).unsqueeze(dim=0)).item())
l=Line()
l.add_xaxis([i for i in range(len(x))])
l.add_yaxis("Original Data",x.tolist())
l.add_yaxis("Pred Data(Using Raw Datas)",x[:ws].tolist()+[i.item() for i in ppre])
l.add_yaxis("Pred Data(Using Pred Datas)",pre)
l.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
l.set_global_opts(title_opts=opts.TitleOpts(title='LSTM CNN'))

l.render_notebook()

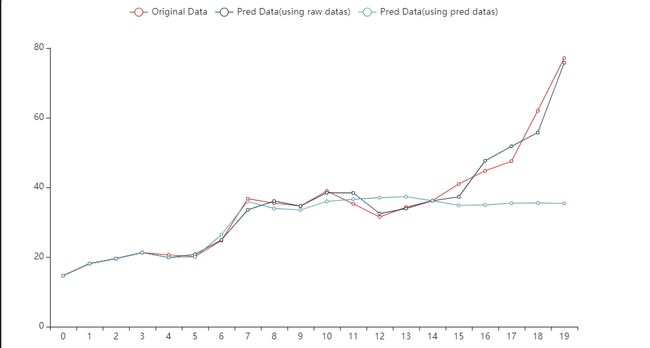
可以发现，用预测做预测的结果，基本上不会差太多，那也就意味着，我们可以对高粱进行预测啦！不过在这之前，我们可以看看用原始数据做训练的结果：

时间窗口一样为6，可以看到在黑线贴合的非常好，但是面对大量缺失的数据，精度就远不如用预测数据做预测的结果了。

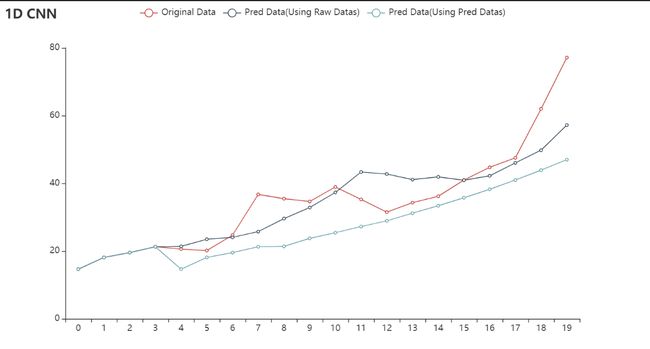
此外，这是用CNN做的结果

我们可以发现LSTM的波动要比CNN好，CNN后面死水一潭，应该是梯度消失导致的，前面信息没有了，后面信息又是自个构造的，这就导致了到后面变成了线性情况。

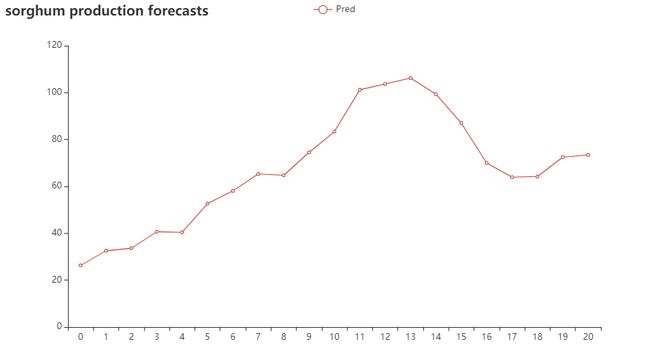
那么最后的最后，就是预测高粱产量了：

pre_data=pp_c[pp_c['Item']=='Sorghum']['Value'].tolist()
l=pre_data[:]
for i in range(len(x)-ws+1):
    l.append(d(torch.FloatTensor(l[-ws:]).unsqueeze(dim=0)).item())
L=Line()
L.add_xaxis([i for i in range(len(x))])
L.add_yaxis("Pred",l)
L.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
L.set_global_opts(title_opts=opts.TitleOpts(title='sorghum production forecasts')
                            
                             )

L.render_notebook()
l.to_csv("path")