杆秤中的数学关系
本文属于个人瞎搞哈,没啥意义。
令我感到好奇的,是杆秤前头的两个钩子和后头的一套刻度。也就是说,这把秤可以只用一套刻度却实现两组质量范围的称量。于是我就想探究一下这其中所包含的数学关系,看看在设计一把秤时,需要考虑些什么。
当然,据我从网上查到的资料来看(只针对一个钩子的杆秤),在制作杆秤时,师傅们可以通过标准质量的砝码来确定刻度,而省去了计算。
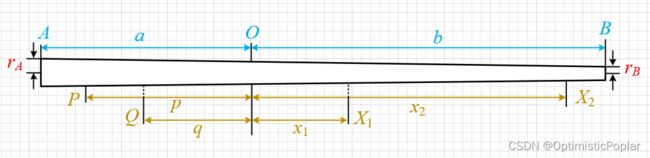
将该问题表述的更加正式、更具有学术味道一些:假设有一根均质长杆,密度为ρ,长杆的形状可近似认为是一个平截正圆锥体。长杆的两个端点分别记为 A A A和 B B B,其中 A A A的横切面半径为 r A {r_A} rA, B B B的横切面半径为 r B {r_B} rB。除此之外,钩子两端还分别用铁皮进行了包裹,用于保护,铁皮的密度为ρ铁,长度分别为 l A {l_A} lA铁和 l B {l_B} lB铁。
现考虑将此长杆用于杆秤的制作,其中支点为 O O O, O A = a OA = a OA=a, O B = b OB=b OB=b。在 O A OA OA段的 P P P点和 Q Q Q点分别安装两个钩子,质量为 m P {m_P} mP和 m Q {m_Q} mQ,用于钩取待测物体。而 O P = p OP = p OP=p, O Q = q OQ = q OQ=q。假设 P P P点较远(所称量的物体质量范围较小),称量范围为 m l l ∼ m l u {m_{ll}} \sim {m_{lu}} mll∼mlu; Q Q Q点可以称量的范围为 m u l ∼ m u u {m_{ul}} \sim {m_{uu}} mul∼muu。杆秤配备一个质量为 m m m砝的砝码,平衡时所在的位置为 X X X点, O X = x OX=x OX=x。刻度上离 O O O点最近和最远的两个点分别为 X 1 {X_1} X1和 X 2 {X_2} X2,同样的, O X 1 = x 1 O{X_1} = {x_1} OX1=x1, O X 2 = x 2 O{X_2} = {x_2} OX2=x2。
解:
针对该问题,尝试采用一个循序渐进的解决策略,先从最简单最理想的情况开始研究,逐步向现实靠近。具体可分为:
1 忽略长杆、铁皮、钩子的质量;
2 考虑质量;
3 考虑长杆形状的影响。
1 忽略长杆、铁皮、钩子的质量
杆秤主要利用的是杠杆原理:
m 1 l 1 = m 2 l 2 (1) {m_1}{l_1} = {m_2}{l_2}\tag{1} m1l1=m2l2(1)
于是可以列写出:

式(2)即为情况1中杆秤所有的数学关系,可以有以下讨论:
(1) m l l : m l u = m u l : m u u = x 1 : x 2 {m_{ll}}:{m_{lu}} = {m_{ul}}:{m_{uu}} = {x_1}:{x_2} mll:mlu=mul:muu=x1:x2。当x1和x2被确定下来后,称量范围的自由度便只剩下1了。两套范围内的四个值任意选定一个,其余三个便无法改变。不过实际中我猜测应该是先考虑称量范围,再选定x1和x2,结论是类似的;
(2) m l l : m u l = m l u : m u u = q : p {m_{ll}}:{m_{ul}} = {m_{lu}}:{m_{uu}} = q:p mll:mul=mlu:muu=q:p。两套称量范围的最大值之比和最小值之比都等于 P P P点和 Q Q Q点的长度之比。考虑三种情况,第一种是先选定小称量范围,此时还可以任意选定大称量范围中的最大质量或最小质量(自由度剩1),但是与之相对的另一个值被随之确定下来。同时, P P P点和 Q Q Q点的长度之比也无法改变了。至于长度的绝对值,不管是 O A OA OA段的点,还是 O B OB OB段的刻度,都与砝码质量有关;第二种情况是先选定两套范围的最小值(或最大值),那么与之相对的最大值(或最小值)之比被确定下来,自由度剩下1。第三种情况,考虑一个最大值和另一个范围中的最小值,那么此时其实和情况一类似,自由度剩下1。
从以上讨论可知:当先设计质量范围时,可以任意选择三个质量,最后一个质量随之确定,此时的两组长度之比也可以确定,但仅仅是长度之比,因为具体的值还需要有砝码的质量数据。
为了便于理解,举例说明。假设 m u l = 2 k g , m u u = 8 k g , m l l = 0.5 k g {m_{ul}} = 2kg,\;{m_{uu}} = 8kg,\;{m_{ll}} = 0.5kg mul=2kg,muu=8kg,mll=0.5kg,此时可求得: m l u = 2 k g {m_{lu}} = 2kg mlu=2kg, x 1 : x 2 = 1 : 4 {x_1}:{x_2} = 1:4 x1:x2=1:4, p : q = 4 : 1 p:q = 4:1 p:q=4:1。如果拿一个 0.8 k g 0.8kg 0.8kg的砝码,且取 x 1 = 0.1 m {x_1} = 0.1{\rm{m}} x1=0.1m,那么有: x 2 = 0 . 4 m , p = 0.16 m , q = 0.04 m {x_2}{\rm{ = 0}}{\rm{.4m}},\;p = 0.16{\rm{m}},\;q = 0.04{\rm{m}} x2=0.4m,p=0.16m,q=0.04m。
有一个有趣的现象值得注意:如果设置某一套范围的最大最小值之比和最大值(或最小值)之比相同,即: ( m l l : m l u ) o r ( m u l : m u u ) = ( m l l : m u l ) o r ( m l u : m u u ) ({m_{ll}}:{m_{lu}})\;or\;({m_{ul}}:{m_{uu}}) = ({m_{ll}}:{m_{ul}})\;or\;({m_{lu}}:{m_{uu}}) (mll:mlu)or(mul:muu)=(mll:mul)or(mlu:muu),那么较小范围的最大值将等于较大范围的最小值,即: m l u = m u l {m_{lu}} = {m_{ul}} mlu=mul。
2 考虑质量以及长杆的粗细变化
此时要考虑各部分的重心问题,因为铁皮这个因素其实和钩子、杆子对系统的影响机理是一致的,为了简单起见,忽略铁皮的质量(也足以说明问题)。
杆子近似为平截正圆锥体,先给出求该形状重心和质量的一般公式:(来源于“机械设计云平台”)
s = h 4 R 2 + 2 R r + 3 r 2 R 2 + R r + r 2 (3) s = {h \over 4}{{{R^2} + 2Rr + 3{r^2}} \over {{R^2} + Rr + {r^2}}}\tag{3} s=4hR2+Rr+r2R2+2Rr+3r2(3)
m = π h ( R 2 + R r + r 2 ) 3 ρ (4) m = {{\pi h({R^2} + Rr + {r^2})} \over 3}\rho \tag{4} m=3πh(R2+Rr+r2)ρ(4)
其中 s s s表示重心离下底(半径为 R R R)的距离(很显然重心在各个横切面圆圆心组成的直线上)。
假设长杆的粗细线性变化,那么其在 O O O点的半径 r O {r_O} rO为:
r O = a r B + b r A a + b (5) {r_O} = {{a{r_B} + b{r_A}} \over {a + b}}\tag{5} rO=a+barB+brA(5)
假设 O A OA OA和 O B OB OB的重心分别位于 S A {S_A} SA和 S B {S_B} SB, O S A = s A O{S_A} = {s_A} OSA=sA, O S B = s B O{S_B} = {s_B} OSB=sB。那么根据式(3),可以求得:
s A = a 4 r O 2 + 2 r O r A + 3 r A 2 r O 2 + r O r A + r A 2 (6) {s_A} = {a \over 4}{{r_O^2 + 2{r_O}{r_A} + 3r_A^2} \over {r_O^2 + {r_O}{r_A} + r_A^2}}\tag{6} sA=4arO2+rOrA+rA2rO2+2rOrA+3rA2(6)
s B = b 4 r O 2 + 2 r O r B + 3 r B 2 r O 2 + r O r B + r B 2 (7) {s_B} = {b \over 4}{{r_O^2 + 2{r_O}{r_B} + 3r_B^2} \over {r_O^2 + {r_O}{r_B} + r_B^2}}\tag{7} sB=4brO2+rOrB+rB2rO2+2rOrB+3rB2(7)
列写出符合此时系统的杠杆平衡原理方程式:
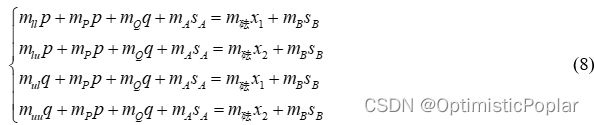
观察式(8),与式(2)相比,每个方程都多出了一些常数项。理想情况下,在不悬挂砝码和待测物体时,杆秤应该处于自然水平的状态,即:
Δ T = ( m P p + m Q q + m A s A ) − ( m B s B ) = 0 (9) \Delta T = ({m_P}p + {m_Q}q + {m_A}{s_A}) - ({m_B}{s_B}) = 0\tag{9} ΔT=(mPp+mQq+mAsA)−(mBsB)=0(9)
此种情况下可以忽略这些常数项的影响,式(8)和式(2)也随之等价。
但在设计制造时肯定会有误差,造成 Δ T ≠ 0 \Delta T \ne 0 ΔT=0,此时式(8)可进一步写为

此时已经没有 m l l : m l u = m u l : m u u = x 1 : x 2 {m_{ll}}:{m_{lu}} = {m_{ul}}:{m_{uu}} = {x_1}:{x_2} mll:mlu=mul:muu=x1:x2,取而代之的是
( m l l p + Δ T ) : ( m l u p + Δ T ) = ( m u l q + Δ T ) : ( m u u q + Δ T ) = x 1 : x 2 ({m_{ll}}p + \Delta T):({m_{lu}}p + \Delta T) = ({m_{ul}}q + \Delta T):({m_{uu}}q + \Delta T) = {x_1}:{x_2} (mllp+ΔT):(mlup+ΔT)=(mulq+ΔT):(muuq+ΔT)=x1:x2;但是仍有 m l l : m u l = m l u : m u u = q : p {m_{ll}}:{m_{ul}} = {m_{lu}}:{m_{uu}} = q:p mll:mul=mlu:muu=q:p。
不管什么情况,杆秤上的刻度分布应当都是均匀的,即如果每次增加的质量一样,那么每次增加的刻度量也不变:
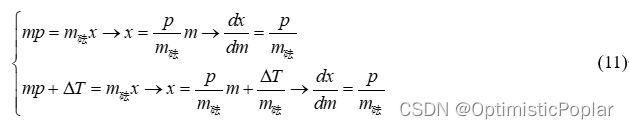
如果说一把秤在设计时没有考虑 Δ T \Delta T ΔT,尝试估算额外力矩带来的测量误差。杆秤初步数据采用情况1中的案例。取杆秤的密度 ρ = 0.5 k g / m 3 \rho = 0.5kg/{m^3} ρ=0.5kg/m3, a = 0.2 m , b = 0.5 m , r A = 0.008 m , r B = 0.004 m , m P = m Q = 0.01 k g a = 0.2m,\;b = 0.5m,\;{r_A} = 0.008m,\;{r_B} = 0.004m,\;{m_P} = {m_Q} = 0.01kg a=0.2m,b=0.5m,rA=0.008m,rB=0.004m,mP=mQ=0.01kg,相对误差公式为:
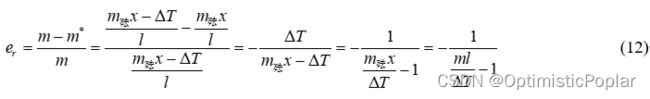
一般来说 Δ T \Delta T ΔT的绝对值是比较小的,因此当 Δ T < 0 \Delta T < 0 ΔT<0时,所测得的质量应比实际质量大;当 Δ T > 0 \Delta T > 0 ΔT>0时,所测得的质量比实际质量小;另外,在同一个钩子下,称量的物体越重,误差越小;钩子离 O O O点越远,误差也越小。(这种情况在现实生活中不会发生,因为现实中的杆秤是利用多个标准砝码来确定刻度准星的)
经过计算,有:
e r l l = − 2.56 % , e r l u = − 0.63 % , e r u l = − 2.56 % , e r u u = − 0.63 % (13) {e_{rll}} = - 2.56\% ,\;{e_{rlu}} = - 0.63\% ,\;{e_{rul}} = - 2.56\% ,\;{e_{ruu}} = - 0.63\% \tag{13} erll=−2.56%,erlu=−0.63%,erul=−2.56%,eruu=−0.63%(13)
与前文讨论一致。
3 考虑长杆形状的影响
2中只考虑了长杆的粗细变化带来的质量变化,3中将进一步考虑形状带来的影响。
实际上,这一影响也是可以避免的,只要在设计时,钩子不要固定于长杆底部的表面,而是长杆的中心。 这里纯属研究,还是讨论其影响。
其实此时的影响就是新的力臂要在原力臂的基础上乘以一个系数,为:
cos θ = ( a + b ) 2 − ( r A − r B ) 2 a + b (14) \cos \theta = {{\sqrt {{{(a + b)}^2} - {{({r_A} - {r_B})}^2}} } \over {a + b}}\tag{14} cosθ=a+b(a+b)2−(rA−rB)2(14)
所以此时有

若采用1和2中的数据,可求得:
cos θ = ( a + b ) 2 − ( r A − r B ) 2 a + b = ( 0.2 + 0.5 ) 2 − ( 0.008 − 0.004 ) 2 0.2 + 0.5 ≈ 0.99998367 (16) \cos \theta = {{\sqrt {{{(a + b)}^2} - {{({r_A} - {r_B})}^2}} } \over {a + b}} = {{\sqrt {{{(0.2 + 0.5)}^2} - {{(0.008 - 0.004)}^2}} } \over {0.2 + 0.5}} \approx 0.99998367\tag{16} cosθ=a+b(a+b)2−(rA−rB)2=0.2+0.5(0.2+0.5)2−(0.008−0.004)2≈0.99998367(16)
由此可见,形状影响实在是微小到可以忽略不记。