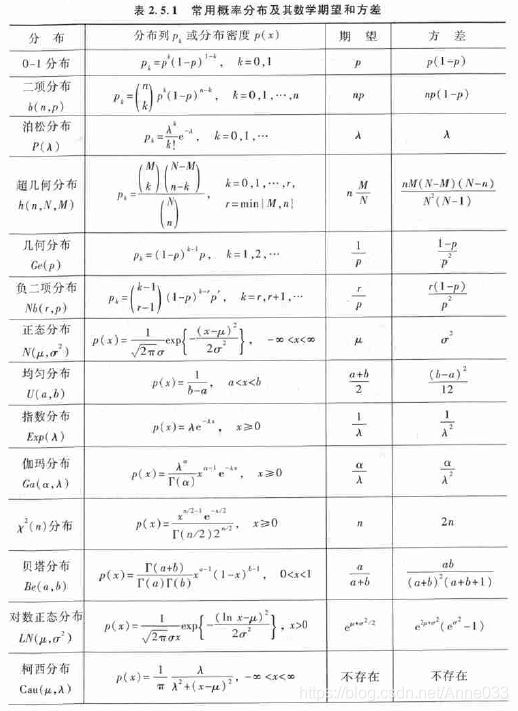
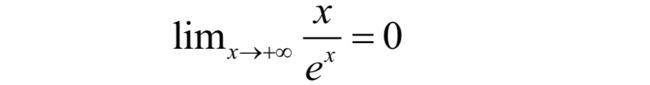概率密度函数、概率分布函数、常见概率分布

1. 概率函数

概率函数，就是用函数的形式来表达概率。
$p_i=P(X=a_i)(i=1,2,3,4,5,6)$
在这个函数里，自变量（X）是随机变量的取值，因变量（$p_i$）是取值的概率。这就叫啥，这叫用数学语言来表示自然现象！它就代表了每个取值的概率，所以顺理成章的它就叫做了X的概率函数。
从公式上来看，概率函数一次只能表示一个取值的概率。比如P（X=1）=1/6,这代表用概率函数的形式来表示，当随机变量取值为1的概率为1/6，一次只能代表一个随机变量的取值。

2. 概率分布

概率分布，就是概率的分布，这个概率分布还是讲概率的。我认为在理解这个概念时，关键不在于“概率”两个字，而在于“分布”这两个字。为了理解“分布”这个词，我们来看一张图。

在很多教材中，这样的列表都被叫做离散型随机变量的“概率分布”。其实严格来说，它应该叫“离散型随机变量的值分布和值的概率分布列表”，这个名字虽然比“概率分布”长了点，但是对于我们这些笨学生来说，肯定好理解了很多。因为这个列表，上面是值，下面是这个取值相应取到的概率，而且这个列表把所有可能出现的情况全部都列出来了！

举个例子吧，一颗6面的骰子，有1，2，3，4，5，6这6个取值，每个取值取到的概率都为1/6。那么你说这个列表是不是这个骰子取值的”概率分布“？

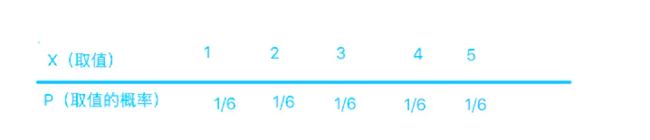
长得挺像的，上面是取值，下面是概率，这应该就是骰子取值的“概率分布”了吧！大错特错！少了一个最重要的条件！对于一颗骰子的取值来说，它列出的不是全部的取值，把6漏掉了!

这么一说你就应该明白概率分布是个什么鬼了吧。

3. 分布函数

说完概率分布，就该说说分布函数了。这个分布函数又是个简化版的东西！我真的很讨厌我们的教材中老是故弄玄虚，卖弄概念！你就老老实实的写成”概率分布函数“，让我们这些笨学生好理解一些不行吗？

看看下图中的分布律！这又是一个不统一叫法的丑恶典型！这里的分布律明明就是我们刚刚讲的“概率函数”，完全就是一个东西嘛！但是我知道很多教材就是叫分布律的。

我们来看看图上的公式，其中的F(x)就代表概率分布函数啦。这个符号的右边是一个长的很像概率函数的公式，但是其中的等号变成了大于等于号的公式。你再往右看看，这是一个一个的概率函数的累加！发现概率分布函数的秘密了吗？它其实根本不是个新事物，它就是概率函数取值的累加结果！所以它又叫累积概率函数！其实，我觉得叫它累积概率函数还更好理解！！

概率函数和概率分布函数就像是一个硬币的两面，它们都只是描述概率的不同手段！

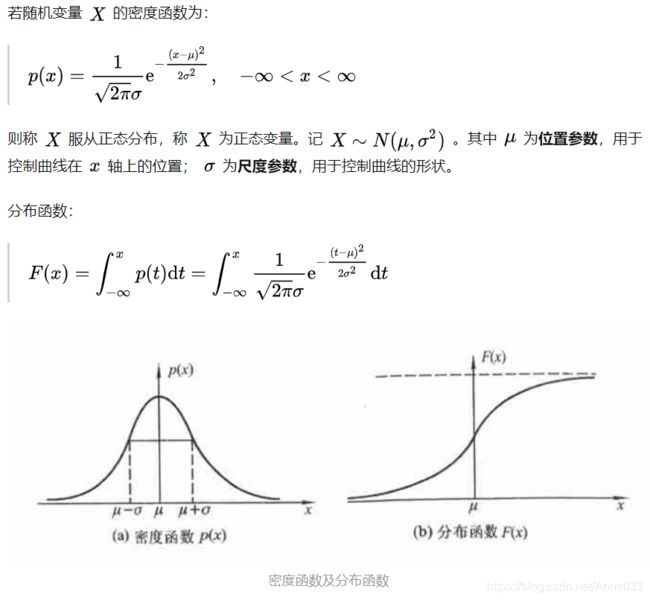
4. 概率密度函数

概率密度函数是概率论中的核心概念之一，用于描述连续型随机变量所服从的概率分布。

4.1 从随机事件说起

研究一个随机变量，不只是要看它能取哪些值，更重要的是它取各种值的概率如何！
回忆我们在学习概率论时的经历，随机事件是第一个核心的概念，它定义为可能发生也可能不发生的事件，因此是否发生具有随机性。例如，抛一枚硬币，可能正面朝上，也可能反面朝上，正面朝上或者反面朝上都是随机事件。掷骰子，1到6这6种点数都可能朝上，每种点数朝上，都是随机事件。

4.2 整数集与实数集

高中时我们学过集合的概念，并且知道整数集是z，实数集是R。对于有限集，可以统计集合中元素的数量即集合的基数（cardinal number，也称为集合的势cardinality）。对于无限集，元素的个数显然是无穷大，但是，都是无穷大，能不能分个三六九等呢？

回忆微积分中的极限，对于下面的极限：

虽然当x趋向于正无穷的时候，x和exp(x)都是无穷大，但它们是有级别的，在exp(x)面前，x是小巫见老巫。

同样的，对于整数集和实数集，也是有级别大小的。任意两个整数之间，如1与2之间，都密密麻麻的分布着无穷多个实数，而且，只要两个实数不相等，不管它们之间有多靠近，如0.0000001和0.0000002，在它们之间还有无穷多个实数。在数轴上，整数是离散的，而实数则是连续的，密密麻麻的布满整个数轴。因此，实数集的元素个数显然比整数要高一个级别。

4.3 随机变量

变量是我们再熟悉不过的概念，它是指一个变化的量，可以取各种不同的值。随机变量可以看做是关联了概率值的变量，即变量取每个值有一定的概率。例如，你买彩票，最后的中奖金额x就是一个随机变量，它的取值有3种情况，以0.9的概率中0元，0.09的概率中100元，0.01的概率中1000元。变量的取值来自一个集合，可以是有限集，也可以是无限集。对于无限集，可以是离散的，也可以是连续的，前者对应于整数集，后者对应于实数集。

4.3.1 离散型随机变量

随机变量是取值有多种可能并且取每个值都有一个概率的变量。它分为离散型和连续型两种，离散型随机变量的取值为有限个或者无限可列个（整数集是典型的无限可列），连续型随机变量的取值为无限不可列个（实数集是典型的无限不可列）。

4.3.2 连续型随机变量

把分布表推广到无限情况，就可以得到连续型随机变量的概率密度函数。此时，随机变量取每个具体的值的概率为0，但在落在每一点处的概率是有相对大小的，描述这个概念的，就是概率密度函数。你可以把这个想象成一个实心物体，在每一点处质量为0，但是有密度，即有相对质量大小。


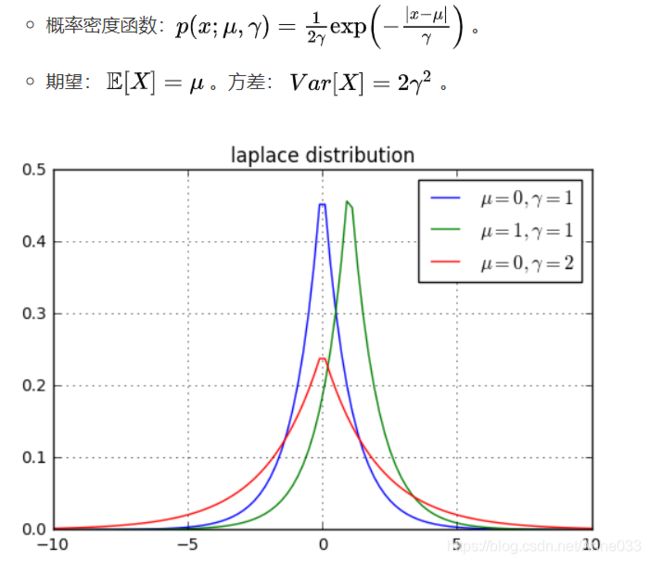
在概率论和统计学中，拉普拉斯是一种连续概率分布。由于它可以看做是俩个不同位置的指数分布背靠背拼在一起，所以它也叫做双指数分布。如果随机变量的概率密度函数分布为：

那么他就是拉普拉斯分布。u为位置参数，b>0是尺度参数。与正态分布相比，正态分布是用相对于u平均值的差的平方来表示，而拉普拉斯概率密度用相对于差的绝对值来表示。因此，拉普拉斯的尾部比正态分布更加平坦。

概率密度函数用数学公式表示就是一个定积分的函数，定积分在数学中是用来求面积的，而在这里，你就把概率表示为面积即可！

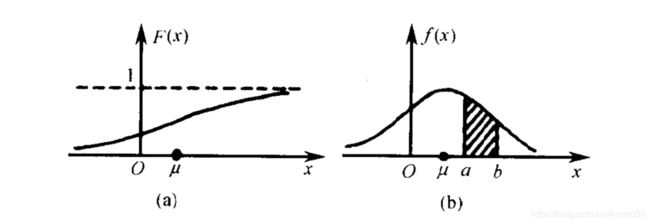
左边是F(x)连续型随机变量分布函数画出的图形，右边是f(x)连续型随机变量的概率密度函数画出的图像，它们之间的关系就是，概率密度函数是分布函数的导函数。

两张图一对比，你就会发现，如果用右图中的面积来表示概率，利用图形就能很清楚的看出，哪些取值的概率更大！这样看起来是不是特别直观，特别爽！！所以，我们在表示连续型随机变量的概率时，用f(x)概率密度函数来表示，是非常好的！

但是，可能读者会有这样的问题：
Q：概率密度函数在某一点的值有什么意义？
A：比较容易理解的意义，某点的 概率密度函数 即为 概率在该点的变化率(或导数)。很容易误以为 该点概率密度值 为 概率值.
比如: 距离(概率)和速度(概率密度)的关系.某一点的速度, 不能以为是某一点的距离，没意义,因为距离是从XX到XX的概念，所以, 概率也需要有个区间.
这个区间可以是x的邻域（可以无限趋近于0）。对x邻域内的f（x）进行积分，可以求得这个邻域的面积，就代表了这个邻域所代表这个事件发生的概率。

4.4 期望E(X)与方差Var(X)

随机变量(Random Variable)X是一个映射，把随机试验的结果与实数建立起了一一对应的关系。而期望与方差是随机变量的两个重要的数字特这。

期望(Expectation, or expected value)是度量一个随机变量取值的集中位置或平均水平的最基本的数字特征；

方差(Variance)是表示随机变量取值的分散性的一个数字特征。 方差越大，说明随机变量的取值分布越不均匀，变化性越强；方差越小，说明随机变量的取值越趋近于均值，即期望值。

4.4.1 期望和方差的运算性质

4.4.1.1 期望运算性质

4.4.1.2 方差的运算性质

4.4.1.3 期望与方差的联系

4.4.2 协方差

4.4.2.1 协方差的运算性质

4.4.3 相关系数

4.4.3.1 定义

相关系数通过方差和协方差定义。两个随机变量的相关系数被定义为：

4.4.3.2 性质

1、有界性
相关系数的取值范围为-1到1，其可以看成是无量纲的协方差。

2、统计意义
值越接近1，说明两个变量正相关性（线性）越强，越接近-1，说明负相关性越强，当为0时表示两个变量没有相关性。

5. 常见概率分布

5.1 均匀分布（Uniform Distribution）

5.2 伯努利分布（Bernoulli Distribution）

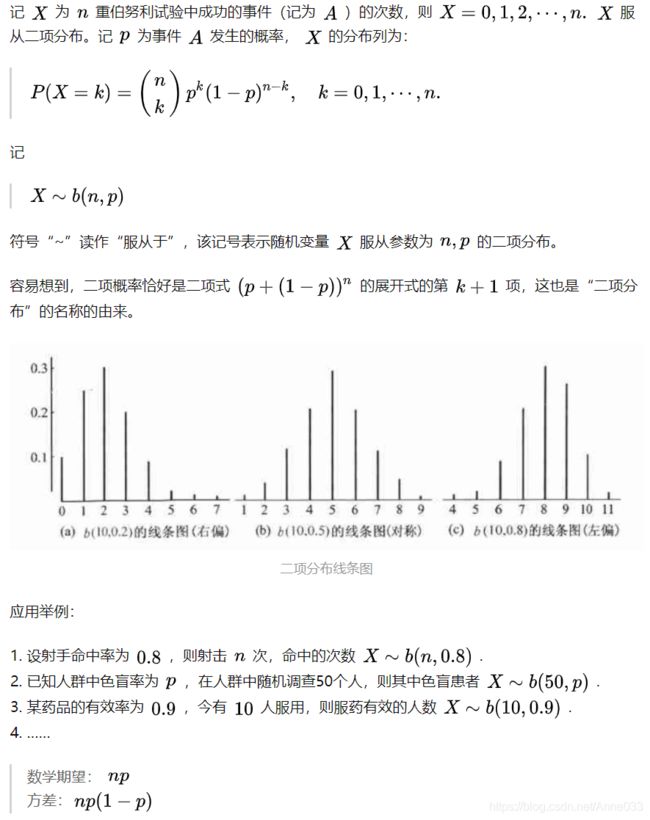
5.3 二项分布（Binomial Distribution）

二项分布(Binomial distribution)是n重伯努利试验成功次数的离散概率分布。

从定义可以看出，伯努利分布是二项分布在n=1时的特例

5.4 负二项分布（Negative Binomial Distribution）

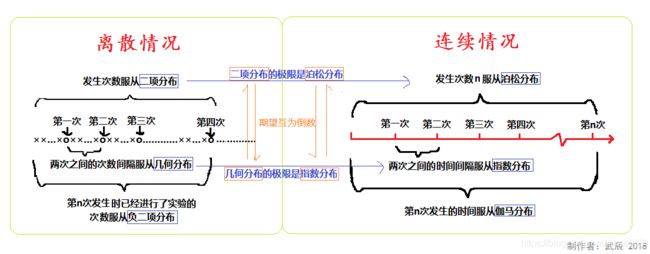
5.5 几何分布（Geometric Distribution）

假定我们有一系列伯努利试验，其中每一个的成功概率为$p$，失败概率为$q=1-p$。在获得一次成功前要进行多次试验？
注意，这里的随机变量的概率分布就是一种几何分布。具体如下：

几何分布的概率分布图如下，见之会有更形象地认知。

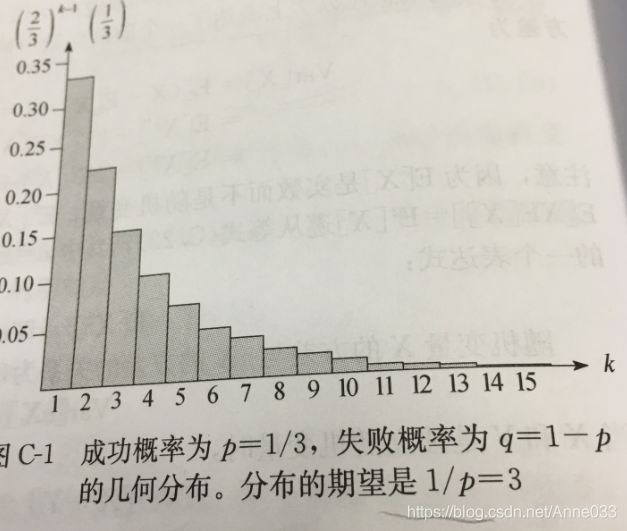
为什么单独把几何分布和二项分布单独列出，一方面其代表的概率试验的普适性，另一方面其期望和方差都是有特殊技巧。

其实有意思的是，这里面的求解过程；但是本文不具体涉及了。因为像几何分布和二项分布这种可能要多写几章，当然是否连续写就不知道了。本着实用主义来。
一般简单地肯定在前面讲，复杂一些得也更有意思一些的肯定是在后面，比如二项分布明显就在几何分布后面了。

不同于几何分布描述的运行到第几次才成功，二项分布描述是的N次试验里有多少次成功。具体如下：

5.6 超几何分布（Hypergeometric Distibution）

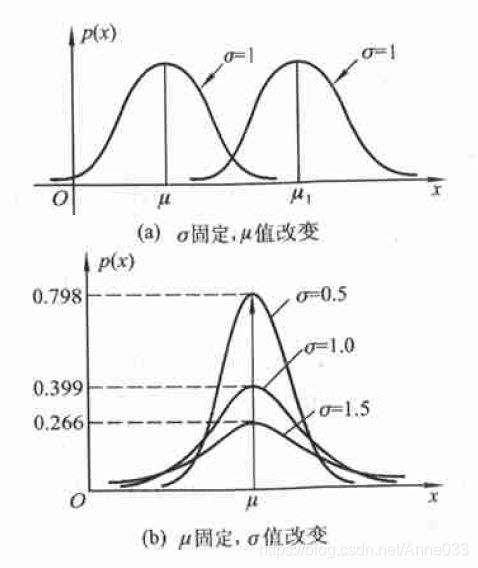
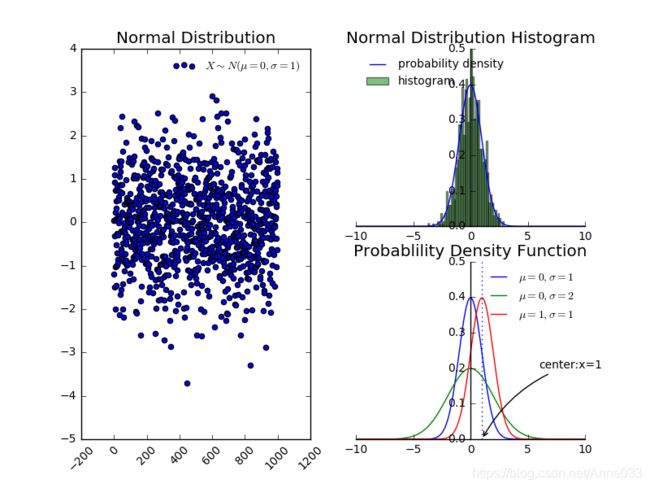
5.7 正态/高斯分布 (Normal / Gaussian Distribution)

正态分布是很多应用中的合理选择。如果某个随机变量取值范围是实数，且对它的概率分布一无所知，通常会假设它服从正态分布。有两个原因支持这一选择：

• 建模的任务的真实分布通常都确实接近正态分布。中心极限定理表明，多个独立随机变量的和近似正态分布。
• 在具有相同方差的所有可能的概率分布中，正态分布的熵最大（即不确定性最大）。

5.7.1 一维正态分布

5.7.2 多维正态分布

5.8 拉普拉斯分布

5.9 泊松分布（Poisson Distribution）

5.10 指数分布

5.11 伽马分布

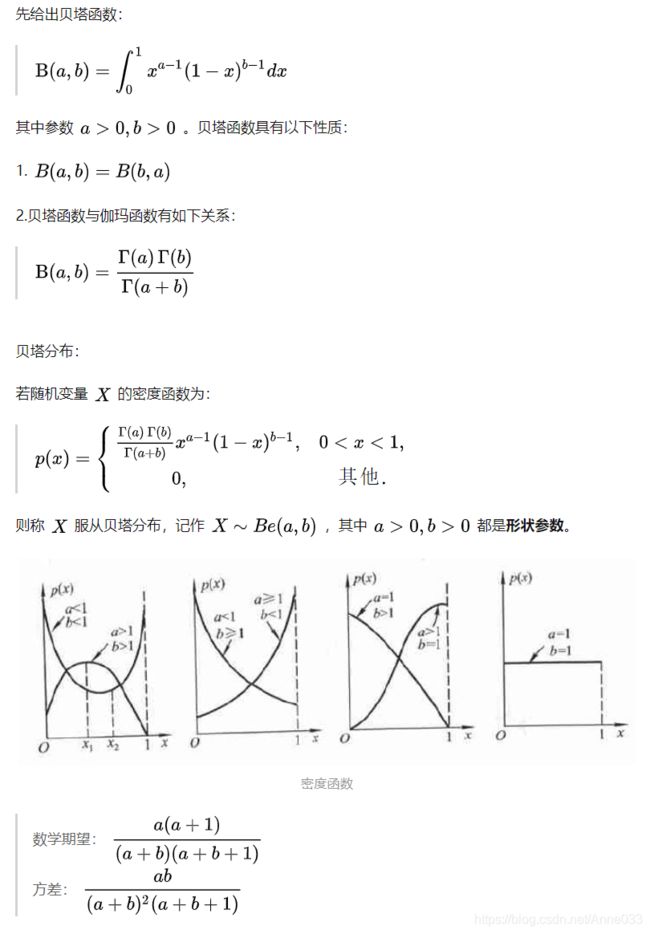
5.12 贝塔分布

5.13 狄拉克分布

5.14 多项式分布与狄里克雷分布

多项式分布(Multinomial Distribution)是二项式分布的推广。二项式做n次伯努利实验，规定了每次试验的结果只有两个，如果现在还是做n次试验，只不过每次试验的结果可以有多m个，且m个结果发生的概率互斥且和为1，则发生其中一个结果X次的概率就是多项式分布。

扔骰子是典型的多项式分布。扔骰子，不同于扔硬币，骰子有6个面对应6个不同的点数，这样单次每个点数朝上的概率都是1/6（对应p1~p6，它们的值不一定都是1/6，只要和为1且互斥即可，比如一个形状不规则的骰子）,重复扔n次，如果问有k次都是点数6朝上的概率就是

5.15 混合概率分布

5.16 总结

https://www.jianshu.com/p/b570b1ba92bb
https://zhuanlan.zhihu.com/p/48140593
https://www.bookstack.cn/read/huaxiaozhuan-ai/spilt.4.6f06ed449f5ed789.md
https://zhuanlan.zhihu.com/p/94181395
https://zhuanlan.zhihu.com/p/64859161
https://blog.csdn.net/touristman5/article/details/56281887
https://zhuanlan.zhihu.com/p/32932782