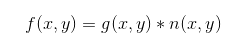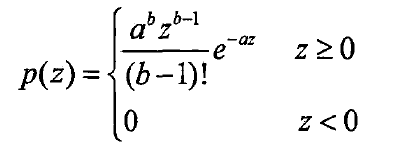图像噪声的特点以及分类(一)
前言:本文根据不同的指标对图像的噪声进行分类。
一、图像噪声的成因
图像在生成和传输过程中常常因受到各种噪声的干扰和影响而是图像降质,这对后续图像的处理和图像视觉效应将产生不利影响。噪声种类很多,比如:电噪声,机械噪声,信道噪声和其他噪声。因此,为了抑制噪声,改善图像质量,便于更高层次的处理,必须对图像进行去噪预处理。
噪声是干扰和妨碍人类认知和理解信息的重要因素,而图像噪声则是图像中干扰和妨碍人类认识和理解图像信息的重要因素。由于噪声本身具有不可预测性,可以将它当做一种随机误差(这种误差只有通过概率统计的方法来识别)。因此,图像噪声可以视为一种多维随机过程,可以选择随机过程的概率分布函数和概率密度函数来作为对图像噪声进行描述的方法。
图像平滑的目的有两个,消除噪声和图像平滑。
二、图像噪声的特征
图像噪声使得图像模糊,甚至淹没图像特征,给分析带来困难。
图像噪声一般具有以下特点:
- 噪声在图像中的分布和大小不规则,即具有随机性。
- 噪声与图像之间一般具有相关性。例如,摄像机的信号和噪声相关,黑暗部分噪声大,明亮部分噪声小。又如,数字图像中的量化噪声与图像相位相关,图像内容接近平坦时,量化噪声呈现伪轮廓,但图像中的随机噪声会因为颤噪效应反而使量化噪声变得不很明显。
- 噪声具有叠加性。在串联图像传输系统中,各部分窜入噪声若是同类噪声可以进行功率相加,依次信噪比要下降。
三、图像噪声的分类
3.1 加性噪声和乘性噪声
按噪声和信号之间的关系,图像噪声可分为加性噪声和乘性噪声。为了分析处理方便,往往将乘性噪声近似认为是加性噪声,而且总是假定信号和噪声是互相独立的。
假定信号为S(t),噪声为n(t),如果混合叠加波形是S(t)+n(t)的形式,则称其为加性噪声。加性嗓声和图像信号强度是不相关的,如图像在传输过程中引进的“信道噪声”电视摄像机扫描图像的噪声等。
如果叠加波形为S(t)[1+n(t)]的形式,则称其为乘性噪声。乘性噪声则与信号强度有关,往往随图像信号的变化而变化,如飞点扫描图像中的嗓声、电视扫描光栅、胶片颗粒造成等。
3.2 外部噪声和内部噪声
按照产生原因,图像噪声可分为外部噪声和内部噪声。
(1)外部噪声,即指系统外部干扰以电磁波或经电源串进系统内部而引起的噪声。如外部电气设备产生的电磁波干扰、天体放电产生的脉冲干扰等。
(2)内部噪声,由系统电气设备内部引起的噪声为内部噪声,如内部电路的相互干扰。内部噪声一般又可分为以下四种:(1)由光和电的基本性质所引起的噪声。(2)电器的机械运动产生的噪声。(3)器材材料本身引起的噪声。(4)系统内部设备电路所引起的噪声。
3.3 平稳噪声非平稳噪声
按照统计特性,图像噪声可分为平稳噪声和非平稳噪声。
(1)平稳噪声。统计特性不随时间变化的噪声称为平稳噪声。
(2)非平稳噪声。统计特性随时间变化的噪声称为非平稳噪声。
3.4 其它几类噪声
量化嗓声是数字图像的主要噪声源,其大小显示出数字图像和原始图像的差异,减少这种嗓声的最好办法就是采用按灰度级概率密度函数选择化级的最优化措施。
“椒盐”噪声:此类嗓声如图像切割引起的即黑图像上的白点,白图像上的黑点噪声,在变换域引入的误差,使图像反变换后造成的变换噪声等。
(1)按噪声幅度随时间分布形状来定义,
- 如其幅度分布是按高斯分布的就称其为高斯噪声,而按雷利分布的就称其为雷利噪声。
(2)按噪声频谱形状来命,
- 如频谱均匀分布的噪声称为白噪声;频谱与频率成反比的称为1/f 噪声;而与频率平方成正比的称为三角噪声等等。
(3)根据经常影响图像质量的噪声源又可分电子噪声和光电子噪声。
- 电子噪声:在阻性器件中由于电子随机热运动而造成的电子噪声是三种模型中最简单的。
- 光电子噪声:光电子噪声是由光的统计本质和图像传感器中光电转换过程引起的。
四、根据噪声的概率分布类型进行分类
图像中的噪声根据其概率分布的情况可以分为
- 高斯噪声(Gaussian noise)、
- 脉冲噪声(Impulsive noise)、瑞利噪声(Rayleigh noise)、
- 伽马噪声(Gamma noise)、
- 指数噪声(Exponential noise)
- 均匀噪声(Uniform noise)等各种形式。
4.1 高斯噪声
高斯噪声是所有噪声当作使用最为广泛的,传感器在低照明度或者高温的条件下产生的噪声就属于高斯噪声,电子电路中产生的噪声也属于高斯噪声,还有很多噪声都可以根据高斯分布(正态分布)的形式进行描述。高斯噪声的概率密度函数可以表示为:
其中灰度值用z表示,灰度值的期望值用μ表示,灰度值的标准差用σ表示。高斯噪声的概率密度函数如下图所示:
4.2 脉冲噪声
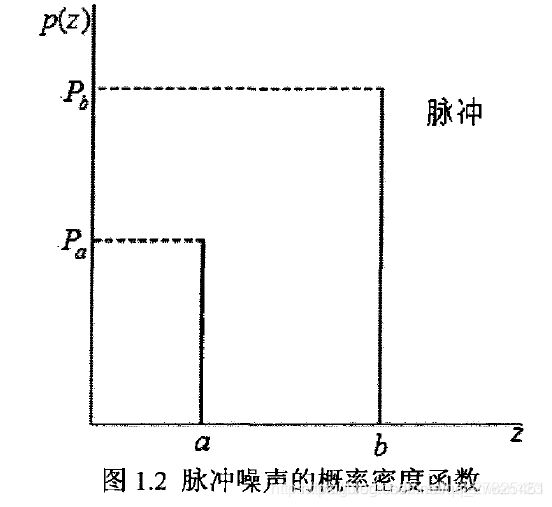
脉冲噪声的概率密度函数可以表示为:
当a
由于传感器本身的物理缺陷导致的hot pixel,weak pixel 或是dead pixel,一般称之为impulse noise,对于impulse noise有单独的处理方法,因为他们不属于随机噪声。
脉冲噪声的概率密度函数分布图:
4.3 瑞利噪声
瑞利噪声的概率密度函数分布为:
瑞利噪声的概率密度函数分布为:
4.4 伽马噪声
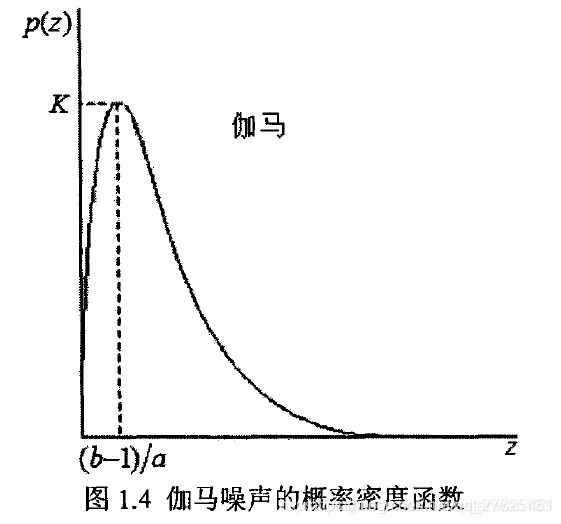
伽马噪声的概率密度函数可以表示为:
其概率密度函数分布图为:
4.5 指数函数
其概率密度函数分布图为:
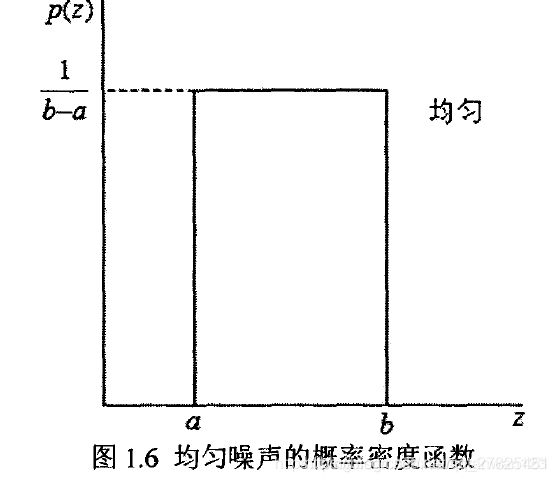
4.6 均匀噪声
其概率密度函数分布为: