数模4—Matlab求最短路和最小生成树

一、最短路问题与Matlab求解

最短路径问题导入

有向图都能解无向图就更容易了啊。
MATLAB求解最短路径：MATLB的graphshortestpath函数
（应该是默认的用floyd方法） 这个函数是可以设置其他方法来求的，但是没啥必要。（比赛的时候注意数据的处理）

Matlab有向图求解

clc;clear;
W = [10,5,2,1,4,6,6,3,9,2];  %非零元素的值  % W是每条边的权值
DG = sparse([1,1,2,2,3,4,4,5,5,5],[2,5,5,3,4,3,1,2,3,4],W);%稀疏矩阵

[dist,path,pred] = graphshortestpath(DG,1,4) %求解所有点间的最短距离(有向)

% biograph生成图对象;  view显示该图
% biograph(邻接矩阵，结点命名，'showWeights','on'在图上显示边权值） 
point_name = ['1','2','3','4','5'];  %结点编号
h = view(biograph(DG,point_name,'showWeights','on')); %生成边和结点的图

%加宽加红
edges = getedgesbynodeid(h,get(h.Nodes(path),'ID'));%根据ID找到结点对应的边  
set(edges,'LineColor',[1 0 0]);%RGB 红绿蓝  1.2其他颜色
set(edges,'LineWidth',2);

%将最短路径的节点和边缘标记为红色并增加线宽
% getedgesbynodeid得到图h的指定边的句柄
%句柄确保能找到对应的东西
% get查询图的属性，h. Nodes(path), 'ID’得到图h中最短路径的边
% set函数设置图形属性
还是会不理解 ‘showWeights’,'on’这些是什么

Matlab无向图求解

clc;clear;
W = [10,5,2,1,4,6,6,3,9,2];  %非零元素的值  % W是每条边的权值
DG = sparse([1,1,2,2,3,4,4,5,5,5],[2,5,5,3,4,3,1,2,3,4],W);%稀疏矩阵
%转为无向图
% 将稀疏矩阵转换成行列矩阵
DG = DG+0
% 转换成对称矩阵
A=DG+DG';
% tril函数：转化为下三角
DG=tril(A)
% 再转换回稀疏矩阵
g=sparse(DG)

% 求节点1到节点4的最短路径  只能是稀疏矩阵
[Dist,Path]=graphshortestpath(g,1,4,'Directed',false) 

%建立无向图
point_name = ['1','2','3','4','5'];  %结点编号
p=biograph(g,point_name,'ShowArrows','off','ShowWeights','on');
h=view(p);  %显示各个路径及权值
 
% 将最短路径的结点以红色显示
set(h.Nodes(Path),'Color',[1 0.4 0.4]);
% 将最短路径的弧以红色显示
edges=getedgesbynodeid(h,get(h.Nodes(Path),'ID'),get(h.Nodes(Path),'ID'));
set(edges,'LineColor',[1 0 0]);
set(edges,'LineWidth',2.0);

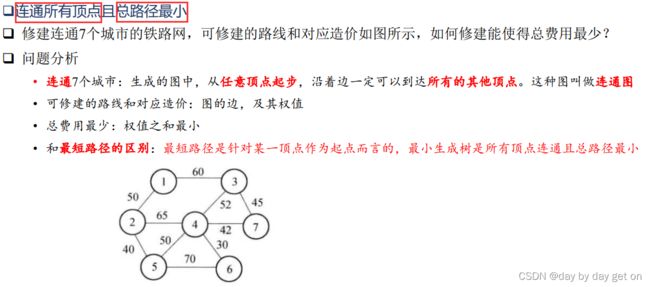
二、最小生成树

最小生成树模型

matlab的minspantree函数求解最小生成树

clc;clear;
s = [1,1,2,2,3,3,4,4,4,5];
t = [2,3,4,5,4,7,5,6,7,6];
weights = [50,60,65,40,52,45,50,30,42,70];
%生成无向图，s和t对应元素代表着边，weights是权值
G = graph(s,t,weights);  %自带函数

T = minspantree(G) %求出最小生成树

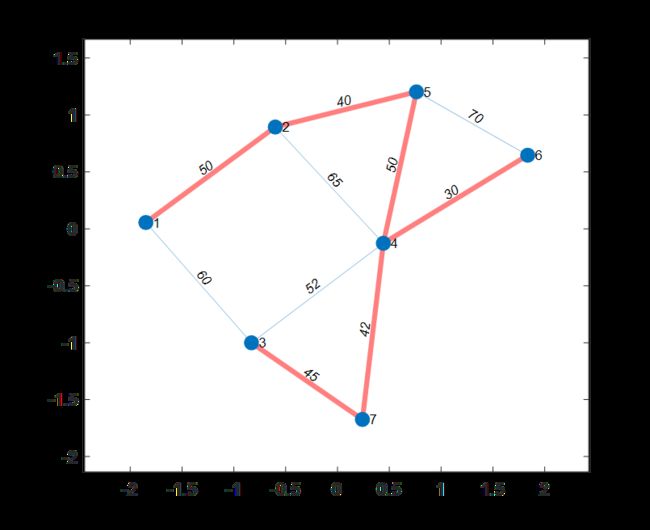
%画出图片  p=plot(G)就能把图展现出来。 后面是设置字体等
%p = plot(G);  %'EdgeLabel',G.Edges.Weight让边显示权值  'MarkerSize',8给结点设置字体大小
p = plot(G,'EdgeLabel',G.Edges.Weight,'MarkerSize',8);
highlight(p,T,'EdgeColor','red','LineWidth',3)

结果;

Kruskal算法（适合点多边少的图）

1.把图G中的所有边全部去掉，得到所有单独的顶点V构成的图T=(V,{})，其中V是顶点集合

2.从G中取出当前权值最小的边，如果该边加入T的边集后T不形成回路，则加入T；否则舍弃

3.重复第2步，直到T中有n-1条边（n是顶点数）

Prim算法（适合边多点少的图）

1.设置一个图U，将原图G中任意一顶点取出加入U中

2.在所在的u∈U，v∈(G-U)的边(g,v)中找到一条权值最小的边，并入图U中

3.重复步骤2，直到U中包含了所有顶点

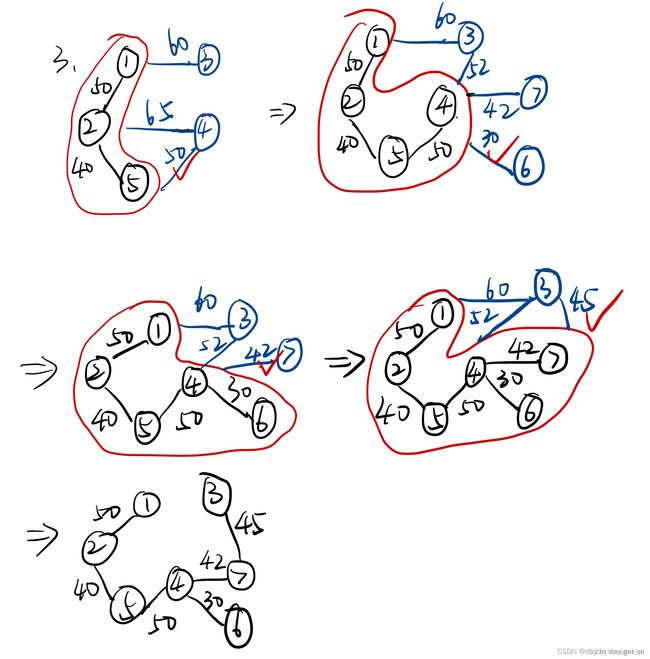
注：若第2步中遇到两条权值相同的最小权值边，任选一条即可，所以最小生成树可能不唯一，但权值之和相同

% 求解最小生成树
T=minspantree(G,"Method","sparse");
% sparse代表的是Kruskal算法
% dense代表的是Prim算法

这有一个图论函数全集：https://blog.csdn.net/weixin_45590473/article/details/107606376

数模版可以导入邻接矩阵的最小生成树代码：

clc;clear;
%W = [.41 .29 .51 .32 .50 .45 .38 .32 .36 .29 .21];
%DG = sparse([1 1 2 2 3 4 4 5 5 6 6],[2 6 3 5 4 1 6 3 4 2 5],W);
%UG = tril(DG + DG');%函数graphminspantree权重输入为下三角矩阵

%这里可以直接输入为邻接矩阵，转为下三角，再转为稀疏矩阵
% 将稀疏矩阵转换成行列矩阵
%DG = DG+0;
% 转换成对称矩阵
A=[0,2,3,4,5;
   2,0,3,4,5;
   3,3,0,4,5;
   4,4,4,0,5;
   5,5,5,5,0]
% tril函数：转化为下三角
DG=tril(A)
% 再转换回稀疏矩阵
g=sparse(DG)

view(biograph(g,[],'ShowArrows','off','ShowWeights','on'));
[ST,pred] = graphminspantree(g,'Method', 'Kruskal');
view(biograph(ST,[],'ShowArrows','off','ShowWeights','on'));

导入矩阵函数：

A =xlsread('G.xlsx')  %导入矩阵