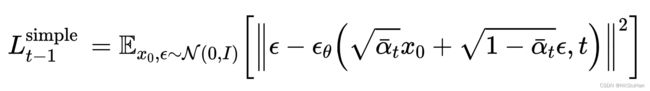《扩散模型 从原理到实战》Hugging Face （一）

---

前言

Hugging Face最近出版了第一本中文书籍《扩散模型 从原理到实战》，其中内容关于扩散模型（Diffusion Model），和AIGC相关的内容较多（Hugging Face的Diffusion课程链接：https://github.com/huggingface/diffusion-models-class）。在这里，记录一下学习过程。
文章内容自用，如有侵权请及时与我联系

---

第一章 扩散模型简介

扩散模型（Diffusion Model）是一类十分先进的基于扩散思想的深度学习生成模型。生成模型除了扩散模型之外，还有出现较早的VAE（Varitational Auto-Encoder，变分自编码器）和GAN（Generative Adversarial Net， 生成对抗网络）等。虽然它们与扩散模型也有一些渊源，不过这并不在本书的讨论范围之内。同时本书也不会深入介绍扩散模型背后复杂的数学原理。即便如此，你依然可以基于本书介绍的内容学会通过相关代码来生成精美图像。

1.1 扩散模型的原理

扩散模型是一类生成模型，他运用物理热力学中的扩散思想，主要包括前向扩散和反向扩散两个过程。本节将介绍扩散模型的原理，其中不包含复杂的数学推导。

1.1.1 生成模型

在深度学习中，生成模型的目标是根据给定的样本（训练数据）生成新样本。首先给定一批训练数据X，假设其服从某种复杂的真实分布p(x)，则给定的训练数据可视为从该分布中才养的观测样本x。如果能够从这些观测样本中估计出训练数据的真实分布，不就可以从该分布中源源不断地采样出新的样本了么？生成模型实际上就是这么做的，它的作用是估计训练数据的真实分布，并将其假定为q(x)。在深度学习中，这个过程称为拟合网络。

那么问题来了，怎么才能知道估计的分布q(x)和这是的分布p(x)的差距大不大呢？一种简单的思路是要求所有的训练数据采样自q(x)的概率最大。这种思路实际上来自统计学中最大似然估计的思想，它也是生成模型的基本思想之一，因此生成模型的学习目标就是对训练数据的分布进行建模。

1.1.2 扩散过程

最大似然估计思想已经在一些模型（如VAE）上应用并取得了不错的效果。扩散模型可看作一个更深层的VAE。扩散模型的表达能力更加丰富，而且其核心在于扩散过程。

扩散的思想来自物理学中的非平衡热力学分支。非平衡热力学专门研究某些不处于热力学平衡中的物理系统，其中最为典型的研究案例是一滴墨水在水中扩散的过程。在扩散开始之前，这地墨水会在水中的某个地方形成一个大的斑点，我们可以认为这是这滴墨水的初始状态，但要描述该初始状态的概率分布则很困难，因为这个概率分布非常复杂。随着扩散过程的进行，这滴墨水随着时间的推移逐步扩散到水中，水的颜色也逐渐变成这滴墨水的颜色。此时，墨水分子的概率分布将变得更加简单和均匀，这样我们就可以很轻松地用数学公式来描述其中的概率分布了。

在这种情况下，非平衡热力学就派上用场了，它可以描述这滴墨水随时间推移的扩散过程中每一个“时间”步（旨在将连续的时间过程离散化）状态的概率分布。若能够想到办法把这个过程反过来，就可以从简单的分布中逐步推断出复杂的分布。

公认最早的扩散模型DDPM（Denosising Diffusion Probabilisitic Model）的扩散原理就由此而来，不过仅有上述条件依然很难从简单的分布倒推出复杂的分布。DDPM还做了一些假设，例如假设扩散过程是马尔可夫过程（即每个时间步状态的概率分布仅由上一个时间步状态的概率分布加上当前时间步的高斯噪声得到），以及假设扩散过程的逆过程是高斯分布。

1）前向过程
前向过程是给数据添加噪声的过程。假设给定一批训练数据，数据分布为x0~q(x0)，其中，0表示初始状态，即还没有开始扩散。如前所述，将前向加噪声的过程分为离散的多个时间步T，在每一个时间步t，给上一个时间步t-1的数据xt-1添加高斯噪声，从而生成带有噪声（简称“带噪”）的数据xt，同时数据xt也会被送入下一个时间步t+1以继续添加噪声。其中，噪声的方差是由一个位于区间(0,1)的固定值βt 确定的，均值则是由固定值βt和当前时刻“带噪”的数据分布确定。在反复迭代和加噪（即添加噪声）T次之后，只要T足够大，根据马尔科夫链的性质，最终就可以得到纯随机噪声分布的数据，即类似稳定墨水系统的状态。

接下来，我们用简单的公式描述一下上述过程。从时间步t-1到时间步t的单步扩散加噪声的数学表达式：

最终的噪声分布数学表达式如下：

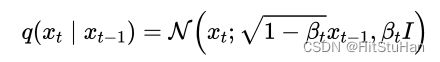
2）反向过程
前向过程是将数据噪声化的过程，反向过程则是“去噪”的过程，即从随机噪声中迭代恢复出清晰数据的过程。

要从采样自高斯噪声的数据xt~N(0,I)的一个随机噪声中恢复出原始数据x0，就需要知道反向过程中每一步的图像分布状态转移。类似地，DDPM也将反向过程定义为一个马尔科夫链，只不过这个马尔科夫链是由一系列用神经网络参数化的高斯分布组成的，也就是需要训练的扩散模型。

从时间步t到时间步t-1的单步反向“去噪”过程的数学表达式如下：

由于反向过程的每一步都是参数化的高斯分布，因此可以分别求高分分布的均值和方差。这里略去根据贝叶斯公式推导的过程，最终得到时间步t-1的高斯分布q(xt-1|xt, x0)的均值和方差的数学表达式如下：

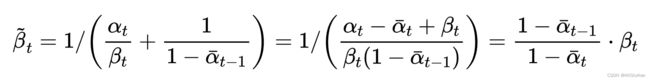
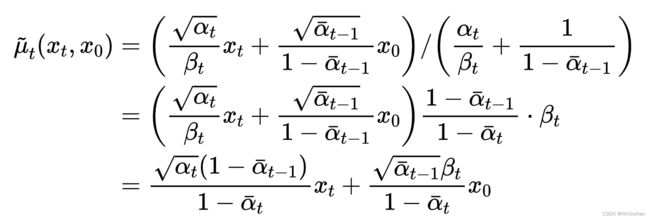
可以看出，方差是一个定量（扩散过程参数固定），而均值是一个依赖于x0和xt的函数，因此需要使用扩散模型来优化参数。

3）优化目标

扩散模型预测的是噪声残差，即要求后向过程中预测的噪声分布与前向过程中施加的噪声分布之间的“距离”最小。

下面我们从另一个角度来看看扩散模型。如果把中间产生的变量看成隐变量的话，那么扩散模型其实是一种包含T个隐变量的模型，因此可以看成更深层次的VAE，而VAE的损失函数可以使用变分推断来得到变分下界（variational lower bound）。至于具体过程，本书不做过多的公式推导，感兴趣的读者可以参考DDPM原文。

扩散模型的最终优化目标的数学表达式如下：

可以看出，在训练DDPM时，只要用一个简单的MSE（Mean Squared Error， 均方误差）损失来最小化前向过程施加的噪声分布和后向过程预测的噪声分布，就能实现最终的优化目标。