傅里叶变换
文章目录
- 傅里叶变换
-
- 傅里叶级数
-
- 傅里叶级数的一般形式
- 周期为2π推导
- a 0 a_0 a0推导
- a n a_n an推导
- b n b_n bn推导
- 周期为任意
- 傅里叶变换
-
- cos x和sin x
- 欧拉公式的表示代入傅里叶级数中
- 对于周期信号
- 对于非周期信号
- 离散傅里叶变换 (DFT) 一维数据
-
- 离散傅里叶变换 (DFT)
-
- 推导过程
- 一维傅里叶变换 - 直接计算
- 离散逆傅里叶变换 (IDFT)
-
- 一维傅里叶逆变换 - 直接计算
- 幅度谱(振幅谱)和相位谱
- std::abs
- std::arg
- std::polar
- 离散傅里叶变换-矩阵乘法表示
-
- 一维傅里叶变换 - 矩阵计算
- 离散傅里叶逆变换-矩阵乘法表示
-
- 一维傅里叶逆变换 - 矩阵计算
- 共轭矩阵和逆矩阵
-
- 共轭矩阵
- 逆矩阵
- 共轭转置(Hermitian转置)
- 代码演示:矩阵计算
- 离散傅里叶变换 (2D DFT) 二维数据
-
- 离散傅里叶变换 (2D DFT)
-
- 二维傅里叶变换 - 直接计算
- 二维傅里叶变换 - 矩阵计算
- 二维离散傅里叶逆变换(2D IDFT)
-
- 二维傅里叶逆变换 - 直接计算
- 二维傅里叶逆变换 - 矩阵计算
- 幅度谱(振幅谱)和相位谱
- 振幅谱移动到中心
-
- 二维离散傅里叶`变换之前` 操作实现
- 二维离散傅里叶`变换之后` 操作实现
- 增强振幅谱显示效果(方便观测)
-
- 1. 对数缩放
- 2. 幂律缩放
- 3. 归一化
- 整合在一起
- 离散快速傅里叶变换(FFT)
-
- FFT视频强烈推荐
- FFT代码实现:
傅里叶变换
傅里叶级数
周期 角频率 频率 振幅 初相角
三角函数正交性
微积分
欧拉公式

傅里叶级数的概念可以追溯到18世纪,由法国数学家让-巴蒂斯特·约瑟夫·傅里叶首次引入。他的目标是使用正弦和余弦函数的级数来表示更复杂的函数。
- 给定一般形式的周期函数
f ( t ) = ∑ n = 0 ∞ A n sin ( n ω t + ψ n ) f(t) = \sum_{n=0}^\infty A_n \sin(n\omega t + \psi_n) f(t)=∑n=0∞Ansin(nωt+ψn)
- 振幅 A n A_n An 描述了每个正弦分量的大小。
- 角频率 n ω n\omega nω 描述了每个正弦分量的速率,其中基本角频率 ω = 2 π T \omega = \frac{2\pi}{T} ω=T2π。
- 相位 ψ n \psi_n ψn 描述了每个正弦分量相对于时间原点的偏移。
傅里叶级数的一般形式
我们可以将其展开为傅里叶级数的一般形式。
-
使用三角恒等式将每一项展开:
A n sin ( n ω t + ψ n ) = A n ( cos ψ n sin n ω t + sin ψ n cos n ω t ) A_n \sin(n\omega t + \psi_n) = A_n (\cos \psi_n \sin n\omega t + \sin \psi_n \cos n\omega t) Ansin(nωt+ψn)=An(cosψnsinnωt+sinψncosnωt) -
将展开的项重新组织:
A n sin ( n ω t + ψ n ) = A n cos ψ n sin n ω t + A n sin ψ n cos n ω t A_n \sin(n\omega t + \psi_n) = A_n \cos \psi_n \sin n\omega t + A_n \sin \psi_n \cos n\omega t Ansin(nωt+ψn)=Ancosψnsinnωt+Ansinψncosnωt -
将系数表示为常见傅里叶系数:
a n = A n sin ψ n a_n = A_n \sin \psi_n an=Ansinψn
b n = A n cos ψ n b_n = A_n \cos \psi_n bn=Ancosψn -
将所有项合并:
f ( t ) = ∑ n = 1 ∞ ( a n sin n ω t + b n cos n ω t ) f(t) = \sum_{n=1}^\infty (a_n \sin n\omega t + b_n \cos n\omega t) f(t)=∑n=1∞(ansinnωt+bncosnωt)
即:
f ( t ) = A 0 sin ψ 0 + A 0 cos ψ 0 + ∑ n = 1 ∞ ( a n sin n ω t + b n cos n ω t ) f(t) = A_0 \sin \psi_0+A_0 \cos \psi_0 + \sum_{n=1}^\infty (a_n \sin n\omega t + b_n \cos n\omega t) f(t)=A0sinψ0+A0cosψ0+∑n=1∞(ansinnωt+bncosnωt)
并注意到 sin ψ 0 = 0 \sin \psi_0 = 0 sinψ0=0,因为 n = 0 n = 0 n=0 时,正弦项消失,所以我们可以将常数项包括为:
cos ψ 0 = 1 \cos \psi_0=1 cosψ0=1
f ( t ) = A 0 + ∑ n = 1 ∞ ( a n sin n ω t + b n cos n ω t ) f(t) = A_0 + \sum_{n=1}^\infty (a_n \sin n\omega t + b_n \cos n\omega t) f(t)=A0+∑n=1∞(ansinnωt+bncosnωt)
周期为2π推导
【纯干货数学推导_傅里叶级数与傅里叶变换_Part2_周期为2Pi的函数展开】
角频率 ω = 2 π T \omega = \frac{2\pi}{T} ω=T2π。周期 T = 2 π {T}={2\pi} T=2π时。角频率被设置为1,并且我们有以下的级数表示:
f ( x ) = ∑ n = 0 ∞ A n sin ( n x + ψ n ) f(x) = \sum_{n=0}^\infty A_n \sin(nx + \psi_n) f(x)=∑n=0∞Ansin(nx+ψn)
这是一个波形的泛波表示,其中每一项都可以看作具有不同频率、振幅和相位的正弦波的叠加。
我们可以使用前面讨论的方法来展开这个表示:
-
使用三角恒等式展开正弦的和:
sin ( α + β ) = sin α cos β + cos α sin β \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta sin(α+β)=sinαcosβ+cosαsinβ -
将每一项展开:
A n sin ( n x + ψ n ) = A n sin n x cos ψ n + A n cos n x sin ψ n A_n \sin(nx + \psi_n) = A_n \sin nx \cos \psi_n + A_n \cos nx \sin \psi_n Ansin(nx+ψn)=Ansinnxcosψn+Ancosnxsinψn -
重新组织项并定义新的常数:
a n = A n cos ψ n a_n = A_n \cos \psi_n an=Ancosψn
b n = A n sin ψ n b_n = A_n \sin \psi_n bn=Ansinψn -
合并所有项:
f ( x ) = ∑ n = 0 ∞ ( a n sin n x + b n cos n x ) f(x) = \sum_{n=0}^\infty (a_n \sin nx + b_n \cos nx) f(x)=∑n=0∞(ansinnx+bncosnx)
即:
f ( t ) = A 0 sin ψ 0 + A 0 cos ψ 0 + ∑ n = 1 ∞ ( a n sin n t + b n cos n t ) f(t) = A_0 \sin \psi_0+A_0 \cos \psi_0 + \sum_{n=1}^\infty (a_n \sin n t + b_n \cos n t) f(t)=A0sinψ0+A0cosψ0+∑n=1∞(ansinnt+bncosnt)
并注意到 sin ψ 0 = 0 \sin \psi_0 = 0 sinψ0=0,因为 n = 0 n = 0 n=0 时,正弦项消失,所以我们可以将常数项包括为:
cos ψ 0 = 1 \cos \psi_0=1 cosψ0=1
f ( t ) = A 0 + ∑ n = 1 ∞ ( a n sin n t + b n cos n t ) f(t) = A_0 + \sum_{n=1}^\infty (a_n \sin n t + b_n \cos n t) f(t)=A0+∑n=1∞(ansinnt+bncosnt)
a 0 a_0 a0推导
我们可以通过以下方法来计算 a 0 a_0 a0:
-
等式两边在 − π 到 π {-}{\pi} 到 {\pi} −π到π周期上积分:
∫ − π π f ( x ) d x = ∫ − π π ( a 0 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) ) d x \int_{-\pi}^{\pi} f(x) \,dx = \int_{-\pi}^{\pi} \left( {a_0} + \sum_{n=1}^{\infty} (a_n \cos nx + b_n \sin nx) \right) \,dx ∫−ππf(x)dx=∫−ππ(a0+∑n=1∞(ancosnx+bnsinnx))dx -
将求和拆开并分别积分:
∫ − π π f ( x ) d x = a 0 π ∫ − π π 1 d x + ∑ n = 1 ∞ ( a n ∫ − π π cos n x d x + b n ∫ − π π sin n x d x ) \int_{-\pi}^{\pi} f(x) \,dx = \frac{a_0}{\pi}\int_{-\pi}^{\pi} 1\,dx + \sum_{n=1}^{\infty} \left( a_n \int_{-\pi}^{\pi} \cos nx\,dx + b_n \int_{-\pi}^{\pi} \sin nx\,dx \right) ∫−ππf(x)dx=πa0∫−ππ1dx+∑n=1∞(an∫−ππcosnxdx+bn∫−ππsinnxdx) -
使用三角函数的正交性:对于任何整数 m m m和 n n n,我们有
∫ − π π cos m x sin n x d x = ∫ − π π sin m x sin n x d x = ∫ − π π cos m x cos n x d x = 0 if m ≠ n \int_{-\pi}^{\pi} \cos mx \sin nx \,dx = \int_{-\pi}^{\pi} \sin mx \sin nx \,dx = \int_{-\pi}^{\pi} \cos mx \cos nx \,dx = 0 \, \text{if } m \neq n ∫−ππcosmxsinnxdx=∫−ππsinmxsinnxdx=∫−ππcosmxcosnxdx=0if m=n
由于 n ≥ 1 n \geq 1 n≥1,我们可以得出所有正弦和余弦项的积分为零。 -
计算剩余的积分:
a 0 ∫ − π π 1 d x = a 0 ⋅ 2 π = a 0 2 π {a_0}\int_{-\pi}^{\pi} 1\,dx = {a_0} \cdot 2\pi = a_02\pi a0∫−ππ1dx=a0⋅2π=a02π
因此,我们得到:
a 0 = 1 2 π ∫ − π π f ( x ) d x a_0 = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(x) \,dx a0=2π1∫−ππf(x)dx
当 a 0 = 1 π ∫ − π π f ( x ) d x a_0 = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x) \,dx a0=π1∫−ππf(x)dx。
那么源函数:
∫ − π π f ( x ) d x = ∫ − π π ( a 0 2 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) ) d x \int_{-\pi}^{\pi} f(x) \,dx = \int_{-\pi}^{\pi} \left( \frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n \cos nx + b_n \sin nx) \right) \,dx ∫−ππf(x)dx=∫−ππ(2a0+∑n=1∞(ancosnx+bnsinnx))dx
这就是傅里叶级数展开中常数项 a 0 a_0 a0的表达式。
a n a_n an推导
当然,我们可以推导傅里叶级数展开中的余弦系数 a n a_n an。对于周期为 2 π 2\pi 2π 的周期函数 f ( x ) f(x) f(x),我们可以找到每个 n n n 的 a n a_n an 如下:
-
两边乘以 cos m x \cos mx cosmx 并在周期为 2 π 2\pi 2π上积分:
∫ − π π f ( x ) cos m x d x = ∫ − π π ( a 0 2 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) ) cos m x d x \int_{-\pi}^{\pi} f(x) \cos mx \,dx = \int_{-\pi}^{\pi} \left( \frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n \cos nx + b_n \sin nx) \right) \cos mx \,dx ∫−ππf(x)cosmxdx=∫−ππ(2a0+∑n=1∞(ancosnx+bnsinnx))cosmxdx -
将求和拆开并分别积分:
∫ − π π f ( x ) cos m x d x = a 0 2 ∫ − π π cos m x d x + ∑ n = 1 ∞ ( a n ∫ − π π cos n x d x cos m x d x + b n ∫ − π π sin n x cos m x d x ) \int_{-\pi}^{\pi} f(x) \cos mx \,dx = \frac{a_0}{2}\int_{-\pi}^{\pi} \cos mx\,dx + \sum_{n=1}^{\infty} \left( a_n \int_{-\pi}^{\pi} \cos nx\,dx\cos mx\,dx + b_n \int_{-\pi}^{\pi} \sin nx \cos mx\,dx \right) ∫−ππf(x)cosmxdx=2a0∫−ππcosmxdx+∑n=1∞(an∫−ππcosnxdxcosmxdx+bn∫−ππsinnxcosmxdx) -
使用三角函数的正交性:
∫ − π π cos m x sin n x d x = 0 for all m , n \int_{-\pi}^{\pi} \cos mx \sin nx \,dx = 0 \, \text{ for all } m,n ∫−ππcosmxsinnxdx=0 for all m,n
∫ − π π cos m x cos n x d x = { 0 if m ≠ n π if m = n ≠ 0 \int_{-\pi}^{\pi} \cos mx \cos nx \,dx = \begin{cases} 0 & \text{if } m \neq n \\ \pi & \text{if } m = n \neq 0 \end{cases} ∫−ππcosmxcosnxdx={0πif m=nif m=n=0 -
计算剩余的积分 只有 m = n m = n m=n时不等于0:
∫ − π π f ( x ) cos n x d x = 0 + a n ∫ − π π cos 2 n x d x + 0 = a n ⋅ π \int_{-\pi}^{\pi} f(x) \cos nx \,dx = 0 + a_n \int_{-\pi}^{\pi} \cos^2 nx\,dx + 0 = a_n \cdot \pi ∫−ππf(x)cosnxdx=0+an∫−ππcos2nxdx+0=an⋅π
因此,我们得到:
a n = 1 π ∫ − π π f ( x ) cos n x d x a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x) \cos nx \,dx an=π1∫−ππf(x)cosnxdx
这就是傅里叶级数展开中余弦项的系数 a n a_n an 的表达式。
b n b_n bn推导
当然,我们现在来推导傅里叶级数展开中的正弦系数 b n b_n bn。对于周期为 2 π 2\pi 2π 的周期函数 f ( x ) f(x) f(x),我们可以找到每个 n n n 的 b n b_n bn 如下:
-
乘以 sin m x \sin mx sinmx 并在整个周期上积分:
∫ − π π f ( x ) sin m x d x = ∫ − π π ( a 0 2 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) ) sin m x d x \int_{-\pi}^{\pi} f(x) \sin mx \,dx = \int_{-\pi}^{\pi} \left( \frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n \cos nx + b_n \sin nx) \right) \sin mx \,dx ∫−ππf(x)sinmxdx=∫−ππ(2a0+∑n=1∞(ancosnx+bnsinnx))sinmxdx -
将求和拆开并分别积分:
∫ − π π f ( x ) sin m x d x = a 0 2 ∫ − π π sin m x d x + ∑ n = 1 ∞ ( a n ∫ − π π cos n x sin m x d x + b n ∫ − π π sin n x d x sin m x d x ) \int_{-\pi}^{\pi} f(x) \sin mx \,dx = \frac{a_0}{2}\int_{-\pi}^{\pi} \sin mx\,dx + \sum_{n=1}^{\infty} \left( a_n \int_{-\pi}^{\pi} \cos nx \sin mx\,dx + b_n \int_{-\pi}^{\pi} \sin nx\,dx \sin mx\,dx \right) ∫−ππf(x)sinmxdx=2a0∫−ππsinmxdx+∑n=1∞(an∫−ππcosnxsinmxdx+bn∫−ππsinnxdxsinmxdx) -
使用三角函数的正交性:
∫ − π π cos m x sin n x d x = 0 for all m , n \int_{-\pi}^{\pi} \cos mx \sin nx \,dx = 0 \, \text{ for all } m,n ∫−ππcosmxsinnxdx=0 for all m,n
∫ − π π sin m x sin n x d x = { 0 if m ≠ n π if m = n ≠ 0 \int_{-\pi}^{\pi} \sin mx \sin nx \,dx = \begin{cases} 0 & \text{if } m \neq n \\ \pi & \text{if } m = n \neq 0\end{cases} ∫−ππsinmxsinnxdx={0πif m=nif m=n=0又由于 ∫ − π π sin n x d x = 0 \int_{-\pi}^{\pi} \sin nx\,dx = 0 ∫−ππsinnxdx=0,所以第一项的积分消失。
-
计算剩余的积分,只有 m = n m = n m=n时不等于0:
∫ − π π f ( x ) sin n x d x = 0 + 0 + b n ∫ − π π sin 2 n x d x = b n ⋅ π \int_{-\pi}^{\pi} f(x) \sin nx \,dx = 0 + 0 + b_n \int_{-\pi}^{\pi} \sin^2 nx\,dx = b_n \cdot \pi ∫−ππf(x)sinnxdx=0+0+bn∫−ππsin2nxdx=bn⋅π
因此,我们得到:
b n = 1 π ∫ − π π f ( x ) sin n x d x b_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x) \sin nx \,dx bn=π1∫−ππf(x)sinnxdx
这就是傅里叶级数展开中正弦项的系数 b n b_n bn 的表达式。
- 所以:
a 0 = 1 π ∫ − π π f ( x ) d x a_0 = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x) \,dx a0=π1∫−ππf(x)dx
a n = 1 π ∫ − π π f ( x ) cos n x d x a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x) \cos nx \,dx an=π1∫−ππf(x)cosnxdx
b n = 1 π ∫ − π π f ( x ) sin n x d x b_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x) \sin nx \,dx bn=π1∫−ππf(x)sinnxdx
周期为任意
纯干货数学推导_傅里叶级数与傅里叶变换_Part3_周期为2L的函数展开
其中基本角频率 ω = 2 π T \omega = \frac{2\pi}{T} ω=T2π。
根据上述公式和给出的周期为 − L -L −L 到 L L L,我们可以整理以下的关系。
首先,根据给定的周期 − L -L −L 到 L L L,我们可以知道这个周期的长度为 T = 2 L T = 2L T=2L。
然后我们可以整理 a 0 a_0 a0, a n a_n an, 和 b n b_n bn 的公式。
-
由于 a 0 a_{0} a0 与周期的平均值有关,我们可以得到:
a 0 = 2 T ∫ 0 T f ( t ) d t = 1 L ∫ − L L f ( t ) d t . a_{0} = \frac{2}{T}\int_{0}^{T}f(t)dt = \frac{1}{L}\int_{-L}^{L}f(t)dt. a0=T2∫0Tf(t)dt=L1∫−LLf(t)dt. -
类似地, a n a_n an 的公式可以改写为:
a n = 2 T ∫ 0 T f ( t ) cos n w t = 1 L ∫ − L L f ( t ) cos ( n π t L ) d t . a_{n} = \frac{2}{T}\int_{0}^{T}f(t)\cos nwt = \frac{1}{L}\int_{-L}^{L}f(t)\cos\left(\frac{n\pi t}{L}\right)dt. an=T2∫0Tf(t)cosnwt=L1∫−LLf(t)cos(Lnπt)dt. -
对于 b n b_n bn,我们也可以用类似的方式改写:
b n = 2 T ∫ 0 T f ( t ) sin n w t = 1 L ∫ − L L f ( t ) sin ( n π t L ) d t . b_{n} = \frac{2}{T}\int_{0}^{T}f(t)\sin nwt = \frac{1}{L}\int_{-L}^{L}f(t)\sin\left(\frac{n\pi t}{L}\right)dt. bn=T2∫0Tf(t)sinnwt=L1∫−LLf(t)sin(Lnπt)dt.
傅里叶级数的目的是将任何周期为 T T T的函数 f ( t ) f(t) f(t)表示为一系列正弦和余弦函数的组合。下面是完整的傅里叶级数展开:
-
常数项:
a 0 = 2 T ∫ 0 T f ( t ) d t a_0 = \frac{2}{T} \int_{0}^{T} f(t) \,dt a0=T2∫0Tf(t)dt -
余弦项:
a n = 2 T ∫ 0 T f ( t ) cos ( 2 π n t T ) d t a_n = \frac{2}{T} \int_{0}^{T} f(t) \cos\left(\frac{2\pi nt}{T}\right) \,dt an=T2∫0Tf(t)cos(T2πnt)dt
这些是傅里叶级数的余弦部分,每一项对应于基本频率的 n n n倍。 -
正弦项:
b n = 2 T ∫ 0 T f ( t ) sin ( 2 π n t T ) d t b_n = \frac{2}{T} \int_{0}^{T} f(t) \sin\left(\frac{2\pi nt}{T}\right) \,dt bn=T2∫0Tf(t)sin(T2πnt)dt
这些是傅里叶级数的正弦部分,每一项也对应于基本频率的 n n n倍。
将上述部分结合,我们得到完整的傅里叶级数展开:
f ( t ) = a 0 2 + ∑ n = 1 ∞ [ a n cos ( 2 π n t T ) + b n sin ( 2 π n t T ) ] f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left[ a_n \cos\left(\frac{2\pi nt}{T}\right) + b_n \sin\left(\frac{2\pi nt}{T}\right) \right] f(t)=2a0+∑n=1∞[ancos(T2πnt)+bnsin(T2πnt)]
此表示通过无穷多的正弦和余弦波组合来逼近原始函数。实际应用中,可能会对 n n n设置一个有限的上限,以便计算有限数量的项,从而得到原始函数的近似表示。
基于函数的对称性,有时候可以进一步简化这个展开。例如,如果 f ( t ) f(t) f(t)是偶函数,那么所有 b n b_n bn项都为零;如果 f ( t ) f(t) f(t)是奇函数,那么所有 a n a_n an项都为零。
我们可以计算给定的积分:
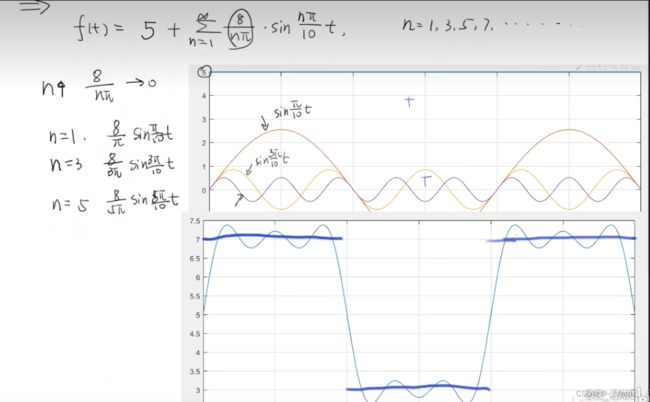
∫ 0 10 7 cos ( n π t 10 ) d t \int_{0}^{10} 7\cos\left(\frac{n\pi t}{10}\right) \,dt ∫0107cos(10nπt)dt
首先,我们可以将常数7提出来,得到:
7 ∫ 0 10 cos ( n π t 10 ) d t 7\int_{0}^{10} \cos\left(\frac{n\pi t}{10}\right) \,dt 7∫010cos(10nπt)dt
接下来,我们可以对里面的余弦项积分。我们可以使用余弦函数的一个基本积分,即:
∫ cos ( a x ) d x = 1 a sin ( a x ) \int \cos(ax) \,dx = \frac{1}{a}\sin(ax) ∫cos(ax)dx=a1sin(ax)
在这里, a = n π 10 a = \frac{n\pi}{10} a=10nπ。所以我们有:
7 ∫ 0 10 cos ( n π t 10 ) d t = 7 [ 10 n π sin ( n π t 10 ) ] 0 10 7\int_{0}^{10} \cos\left(\frac{n\pi t}{10}\right) \,dt = 7\left[ \frac{10}{n\pi}\sin\left(\frac{n\pi t}{10}\right) \right]_{0}^{10} 7∫010cos(10nπt)dt=7[nπ10sin(10nπt)]010
现在,我们可以将上下限代入:
= 7 [ 10 n π sin ( n π ⋅ 10 10 ) − 10 n π sin ( n π ⋅ 0 10 ) ] = 7\left[ \frac{10}{n\pi}\sin\left(\frac{n\pi \cdot 10}{10}\right) - \frac{10}{n\pi}\sin\left(\frac{n\pi \cdot 0}{10}\right) \right] =7[nπ10sin(10nπ⋅10)−nπ10sin(10nπ⋅0)]
因为 sin \sin sin 是周期为 2 π 2\pi 2π 的函数,所以:
= 7 [ 10 n π sin ( n π ) ] = 70 n π sin ( n π ) = 7\left[ \frac{10}{n\pi}\sin(n\pi) \right] = \frac{70}{n\pi}\sin(n\pi) =7[nπ10sin(nπ)]=nπ70sin(nπ)
由于 sin \sin sin 的周期性,对于任何整数 n n n, sin ( n π ) = 0 \sin(n\pi) = 0 sin(nπ)=0。
所以最终答案是:
∫ 0 10 7 cos ( n π t 10 ) d t = 0 \int_{0}^{10} 7\cos\left(\frac{n\pi t}{10}\right) \,dt = 0 ∫0107cos(10nπt)dt=0
傅里叶变换
【纯干货数学推导_傅里叶级数与傅里叶变换_Part4_傅里叶级数的复数形式】
cos x和sin x
通过欧拉公式 e i x = cos x + i sin x e^{ix} = \cos x + i\sin x eix=cosx+isinx,我们可以用复指数来表示 cos x \cos x cosx 和 sin x \sin x sinx。下面是推导过程:
-
对于余弦:
我们可以取欧拉公式的共轭,并将其与原始公式相加,然后除以2来找到余弦的表达式:e − i x = cos x − i sin x e^{-ix} = \cos x - i\sin x e−ix=cosx−isinx
然后将 e i x e^{ix} eix 和 e − i x e^{-ix} e−ix 相加并除以2:
e i x + e − i x 2 = cos x + i sin x + cos x − i sin x 2 = cos x \frac{e^{ix} + e^{-ix}}{2} = \frac{\cos x + i\sin x + \cos x - i\sin x}{2} = \cos x 2eix+e−ix=2cosx+isinx+cosx−isinx=cosx
所以我们得到:
cos x = e i x + e − i x 2 \cos x = \frac{e^{ix} + e^{-ix}}{2} cosx=2eix+e−ix
-
对于正弦:
我们可以采取类似的方法,只是这次将 e i x e^{ix} eix 和 e − i x e^{-ix} e−ix 相减并除以 2 i 2i 2i:e i x − e − i x 2 i = cos x + i sin x − ( cos x − i sin x ) 2 i = 2 i sin x 2 i = sin x \frac{e^{ix} - e^{-ix}}{2i} = \frac{\cos x + i\sin x - (\cos x - i\sin x)}{2i} = \frac{2i\sin x}{2i} = \sin x 2ieix−e−ix=2icosx+isinx−(cosx−isinx)=2i2isinx=sinx
所以我们得到:
sin x = e i x − e − i x 2 i \sin x = \frac{e^{ix} - e^{-ix}}{2i} sinx=2ieix−e−ix
欧拉公式的表示代入傅里叶级数中
当我们将欧拉公式的表示代入傅里叶级数中,我们可以得到傅里叶级数的复指数形式。
我们首先回顾标准傅里叶级数的形式:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n ω t + b n sin n ω t ) f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n \cos n\omega t + b_n \sin n\omega t) f(t)=2a0+∑n=1∞(ancosnωt+bnsinnωt)
然后我们使用上述推导的欧拉公式的结果:
cos n ω t = e i n ω t + e − i n ω t 2 \cos n\omega t = \frac{e^{in\omega t} + e^{-in\omega t}}{2} cosnωt=2einωt+e−inωt
sin n ω t = e i n ω t − e − i n ω t 2 i \sin n\omega t = \frac{e^{in\omega t} - e^{-in\omega t}}{2i} sinnωt=2ieinωt−e−inωt
代入到傅里叶级数中得到:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n e i n ω t + e − i n ω t 2 + b n e i n ω t − e − i n ω t 2 i ) f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left(a_n \frac{e^{in\omega t} + e^{-in\omega t}}{2} + b_n \frac{e^{in\omega t} - e^{-in\omega t}}{2i}\right) f(t)=2a0+∑n=1∞(an2einωt+e−inωt+bn2ieinωt−e−inωt)
我们可以进一步整理这个表达式,将正向和负向的复指数项分组在一起。定义新的复数系数:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n e i n ω t + e − i n ω t 2 + b n e i n ω t − e i n ω t 2 i ) = a 0 2 + ∑ n = 1 ∞ ( a n − i b n 2 e i n ω t + a n + i b n 2 e − i n ω t ) \begin{aligned}f(t) & = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left( a_n \frac{e^{in\omega t} + e^{-in\omega t}}{2} + b_n \frac{e^{in\omega t} - e^{in\omega t}}{2i} \right) \\& = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left( \frac{a_n - ib_n}{2} e^{in\omega t} + \frac{a_n + ib_n}{2} e^{-in\omega t}\right)\end{aligned} f(t)=2a0+n=1∑∞(an2einωt+e−inωt+bn2ieinωt−einωt)=2a0+n=1∑∞(2an−ibneinωt+2an+ibne−inωt)
其中:
c 0 = ∑ n = 0 0 a 0 2 e i n ω t = a 0 2 c_0 = \sum_{n=0}^{0}\frac{a_{0}}{2}e^{\mathrm{in\omega t}}=\frac{a_{0}}{2} c0=∑n=002a0einωt=2a0
c n = a n − i b n 2 c_n = \frac{a_n - ib_n}{2} cn=2an−ibn
c − n = a n + i b n 2 c_{-n} = \frac{a_n + ib_n}{2} c−n=2an+ibn
将这些代入原式,我们可以将傅里叶级数重写为:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( c n e i n ω t + c − n e − i n ω t ) = c 0 + ∑ n = 1 ∞ c n e i n ω t + ∑ n = 1 ∞ c − n e − i n ω t = ∑ n = − ∞ ∞ c n e i n ω t \begin{aligned}f(t) & = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left( c_n e^{in\omega t} + c_{-n} e^{-in\omega t} \right) \\& = c_0 + \sum_{n=1}^{\infty} c_n e^{in\omega t} + \sum_{n=1}^{\infty} c_{-n} e^{-in\omega t} \\& = \sum_{n=-\infty}^{\infty} c_n e^{in\omega t}\end{aligned} f(t)=2a0+n=1∑∞(cneinωt+c−ne−inωt)=c0+n=1∑∞cneinωt+n=1∑∞c−ne−inωt=n=−∞∑∞cneinωt
我们将正项和负项的求和合并为一个从 − ∞ -\infty −∞ 到 ∞ \infty ∞ 的求和。
我们还可以将傅里叶级数写为复数形式:
f ( t ) = ∑ n = − ∞ ∞ c n e i n ω t f(t) = \sum_{n=-\infty}^{\infty} c_n e^{in\omega t} f(t)=∑n=−∞∞cneinωt
其中 c n c_n cn 可以使用以下公式计算:
c n = 1 T ∫ 0 T f ( t ) e − i n ω t d t c_n = \frac{1}{T} \int_{0}^{T} f(t) e^{-in\omega t} \,dt cn=T1∫0Tf(t)e−inωtdt
对于周期信号
如果一个信号具有周期性,即存在某个正数 T T T 使得 f ( t + T ) = f ( t ) f(t + T) = f(t) f(t+T)=f(t) 对所有的 t t t 成立,那么我们可以使用傅里叶级数来表示该信号:
f ( t ) = ∑ n = − ∞ ∞ c n e i n ω t f(t) = \sum_{n=-\infty}^{\infty} c_n e^{in\omega t} f(t)=∑n=−∞∞cneinωt
其中 ω = 2 π T \omega = \frac{2\pi}{T} ω=T2π,且系数 c n c_n cn 由以下公式给出:
c n = 1 T ∫ 0 T f ( t ) e − i n ω t d t c_n = \frac{1}{T} \int_{0}^{T} f(t) e^{-in\omega t} \,dt cn=T1∫0Tf(t)e−inωtdt
对于非周期信号
让我们让周期 T T T 趋于无穷大,并引入角频率 ω = 2 π T \omega = \frac{2\pi}{T} ω=T2π。当 T → ∞ T \to \infty T→∞,我们的离散和变成连续积分,我们得到傅里叶变换:
F ( ω ) = ∫ − ∞ ∞ f ( t ) e − i ω t d t F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} \,dt F(ω)=∫−∞∞f(t)e−iωtdt
同样,我们可以从傅里叶级数的表达式推导出逆傅里叶变换。我们首先将和转换为积分,然后让周期趋于无穷大。结果是:
f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e i ω t d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i\omega t} \,d\omega f(t)=2π1∫−∞∞F(ω)eiωtdω
如果信号不具有周期性,我们不能使用傅里叶级数来表示它,因为没有合适的周期可以使用。在这种情况下,我们可以使用傅里叶变换:
- 从周期到非周期
从傅里叶级数到傅里叶变换的过渡可以通过让周期 T T T 趋于无穷大来实现。在这个极限下,离散频率的和变为连续频率的积分,从而产生了傅里叶变换。
-
总结
-
对于周期信号,我们使用傅里叶级数进行分析。
-
对于非周期信号,我们使用傅里叶变换进行分析。
-
从傅里叶级数到傅里叶变换的过渡可以通过考虑非周期信号并让周期趋于无穷大来实现。
离散傅里叶变换 (DFT) 一维数据
离散傅里叶变换(Discrete Fourier Transform,DFT)是傅里叶变换的离散版本,适用于离散信号。以下是其推导过程。
离散傅里叶变换 (DFT)
- 离散信号
假设我们有一个长度为 N N N的离散信号 x [ n ] x[n] x[n],其中 n = 0 , 1 , 2 , … , N − 1 n = 0, 1, 2, \ldots, N-1 n=0,1,2,…,N−1。
我们想要计算信号的频率分量。DFT的定义为:
X [ k ] = ∑ n = 0 N − 1 x [ n ] ⋅ e − i 2 π k n / N X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-i2\pi kn/N} X[k]=∑n=0N−1x[n]⋅e−i2πkn/N
其中:
- X [ k ] X[k] X[k] 是频率索引为 k k k的频率分量。
- x [ n ] x[n] x[n] 是时间索引为 n n n的时间域样本。
- e − i 2 π k n / N e^{-i2\pi kn/N} e−i2πkn/N 是复指数函数,用于权衡每个时间样本对频率分量的贡献。
推导过程
- 离散时间信号:我们开始于离散时间信号 x [ n ] x[n] x[n],它可以被认为是连续信号的采样版本。
- 周期性:DFT假设信号是周期的,周期为 N N N。
- 频率分析:为了在频域中表示信号,我们使用复指数函数 e − i 2 π k n / N e^{-i2\pi kn/N} e−i2πkn/N与每个时间样本相乘并求和。这个操作实际上是在计算信号在每个离散频率上的响应。
- 正交性:复指数函数的正交性保证了每个频率分量彼此独立。
一维傅里叶变换 - 直接计算
代码实现:
#include 离散逆傅里叶变换 (IDFT)
逆DFT(IDFT)可以用于从频域恢复时域信号,定义为:
x [ n ] = 1 N ∑ k = 0 N − 1 X [ k ] ⋅ e i 2 π k n / N x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \cdot e^{i2\pi kn/N} x[n]=N1∑k=0N−1X[k]⋅ei2πkn/N
f ( m , n ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 F ( u , v ) ⋅ e i 2 π ( u m M + v n N ) f(m, n) = \frac{1}{MN} \sum_{u=0}^{M-1}\sum_{v=0}^{N-1} F(u, v) \cdot e^{i 2\pi\left(\frac{um}{M} + \frac{vn}{N}\right)} f(m,n)=MN1∑u=0M−1∑v=0N−1F(u,v)⋅ei2π(Mum+Nvn)
一维傅里叶逆变换 - 直接计算
代码实现:
#include 幅度谱(振幅谱)和相位谱
离散傅里叶变换(DFT)用于分析离散时间信号的频率成分。计算DFT后,你会得到一组复数,其中每个复数代表信号在一个特定频率下的幅度和相位。幅度谱和相位谱是对这些复数的解释。
- 幅度谱:幅度谱显示信号中各个频率分量的强度或幅度。如果你的DFT的结果是一组复数 X [ k ] X[k] X[k],那么幅度谱是这些复数的绝对值:
∣ X [ k ] ∣ = Re ( X [ k ] ) 2 + Im ( X [ k ] ) 2 |X[k]| = \sqrt{{\text{Re}(X[k])}^2 + {\text{Im}(X[k])}^2} ∣X[k]∣=Re(X[k])2+Im(X[k])2
其中, Re ( X [ k ] ) \text{Re}(X[k]) Re(X[k]) 和 Im ( X [ k ] ) \text{Im}(X[k]) Im(X[k]) 分别是复数 X [ k ] X[k] X[k] 的实部和虚部。
- 相位谱:相位谱显示信号中各个频率分量的相位或角度。相位谱是复数的辐角:
∠ X [ k ] = arctan ( Im ( X [ k ] ) Re ( X [ k ] ) ) \angle X[k] = \arctan\left(\frac{{\text{Im}(X[k])}}{{\text{Re}(X[k])}}\right) ∠X[k]=arctan(Re(X[k])Im(X[k]))
可能还需要根据实部和虚部的符号进行调整,以确保角度位于正确的象限。
这两个谱可以一起提供有关信号频率成分的完整信息。幅度谱告诉你每个频率的强度有多大,而相位谱告诉你每个频率分量是如何相对于其他分量相位移动的。理解幅度和相位谱有助于深入理解信号的结构和行为。
代码实现:
// 从复数矩阵中获取幅度谱和相位谱
void computeSpectra(const std::vector<std::complex<double>>& dft_result,
std::vector<double>& amplitude,
std::vector<double>& phase) {
int N = dft_result.size();
amplitude.resize(N);
phase.resize(N);
for (int i = 0; i < N; ++i) {
amplitude[i] = std::abs(dft_result[i]);
phase[i] = std::arg(dft_result[i]);
}
}
// 从幅度谱和相位谱重构复数矩阵
void recoverDFT(const std::vector<double>& amplitude,
const std::vector<double>& phase,
std::vector<std::complex<double>>& dft_result) {
int N = amplitude.size();
dft_result.resize(N);
for (int i = 0; i < N; ++i) {
dft_result[i] = std::polar(amplitude[i], phase[i]);
}
}
std::abs
std::abs 函数在 C++ 标准库中不仅可以用于整数和浮点数类型,还可以用于复数类型。当用于 std::complex 类型时,std::abs 返回复数的模,也就是绝对值。
下面是一个使用 std::abs 计算复数绝对值的例子:
#include 在这个例子中,复数 z = 3 + 4 i z = 3 + 4i z=3+4i,所以它的模是 3 2 + 4 2 = 5 \sqrt{3^2 + 4^2} = 5 32+42=5。
std::arg
std::arg 是另一个与复数相关的函数,用于计算复数的辐角(或称为相位角)。对于复数 z = a + b i z = a + bi z=a+bi,std::arg(z) 返回的是从正实轴到复数所在位置的角度,单位为弧度。
该角度的范围为 [ − π , π ] [- \pi, \pi] [−π,π],并且与复数在复平面上的位置有关。具体地说,std::arg(z) 返回的是 arctan ( b a ) \arctan\left(\frac{b}{a}\right) arctan(ab)。
下面是一个使用 std::arg 的例子:
#include 在这个例子中,复数 z = 3 + 4 i z = 3 + 4i z=3+4i,所以它的辐角是 arctan ( 4 3 ) ≈ 0.93 \arctan\left(\frac{4}{3}\right) \approx 0.93 arctan(34)≈0.93 弧度。
std::polar
std::polar 函数是用于创建一个复数,给定其模(幅值)和辐角(相位角)。这个函数可以让你从极坐标形式创建一个复数。
函数的签名如下:
template< class T >
std::complex<T> polar( const T& rho, const T& theta = 0 );
其中 rho 是复数的模,theta 是复数的辐角(单位为弧度)。默认情况下,辐角为0。
下面是使用 std::polar 的一个例子:
#include 这个例子使用 std::polar 从给定的模和辐角创建了复数 z = 3 + 4 i z = 3 + 4i z=3+4i。
离散傅里叶变换-矩阵乘法表示
一维傅里叶变换 - 矩阵计算
离散傅里叶变换(DFT)可以通过一个更精确的数学表达式来定义。给定一个长度为 N N N 的复数序列 x [ 0 ] , x [ 1 ] , … , x [ N − 1 ] x[0], x[1], \ldots, x[N-1] x[0],x[1],…,x[N−1],其DFT为 X [ 0 ] , X [ 1 ] , … , X [ N − 1 ] X[0], X[1], \ldots, X[N-1] X[0],X[1],…,X[N−1],其中
X [ k ] = ∑ n = 0 N − 1 x [ n ] ⋅ exp ( − i 2 π k n N ) X[k] = \sum_{n=0}^{N-1} x[n] \cdot \exp\left(-i \frac{2 \pi k n}{N}\right) X[k]=∑n=0N−1x[n]⋅exp(−iN2πkn)
这可以通过矩阵乘法来表示,其中矩阵 F F F 和向量 x x x 的乘积给出了向量 X X X:
X = F ⋅ x X = F \cdot x X=F⋅x
其中矩阵 F F F 的元素由
F j k = exp ( − i 2 π j k N ) F_{jk} = \exp\left(-i \frac{2 \pi j k}{N}\right) Fjk=exp(−iN2πjk)
给出, 0 ≤ j , k < N 0 \leq j, k < N 0≤j,k<N。
具体地说,如果我们有一个长度为4的序列,则DFT矩阵为:
F = [ 1 1 1 1 1 ω ω 2 ω 3 1 ω 2 ω 4 ω 6 1 ω 3 ω 6 ω 9 ] F = \begin{bmatrix} 1 & 1 & 1 & 1\\ 1 & \omega & \omega^2 & \omega^3\\ 1 & \omega^2 & \omega^4 & \omega^6\\ 1 & \omega^3 & \omega^6 & \omega^9 \end{bmatrix} F= 11111ωω2ω31ω2ω4ω61ω3ω6ω9
其中 ω = exp ( − i 2 π 4 ) = i \omega = \exp\left(-i \frac{2 \pi}{4}\right) = i ω=exp(−i42π)=i 是第四单位根。
然后,将输入向量与此矩阵相乘:
[ X [ 0 ] X [ 1 ] X [ 2 ] X [ 3 ] ] = [ 1 1 1 1 1 i − 1 − i 1 − 1 1 − 1 1 − i − 1 i ] [ x [ 0 ] x [ 1 ] x [ 2 ] x [ 3 ] ] \begin{bmatrix} X[0]\\ X[1]\\ X[2]\\ X[3] \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1\\ 1 & i & -1 & -i\\ 1 & -1 & 1 & -1\\ 1 & -i & -1 & i \end{bmatrix} \begin{bmatrix} x[0]\\ x[1]\\ x[2]\\ x[3] \end{bmatrix} X[0]X[1]X[2]X[3] = 11111i−1−i1−11−11−i−1i x[0]x[1]x[2]x[3]
这个乘积给出了频域表示中的复数值。注意,根据具体的定义和约定,DFT的正负号和归一化系数可能会有所不同。上述描述是其中一种常见的形式。
代码实现:
#include 离散傅里叶逆变换-矩阵乘法表示
一维傅里叶逆变换 - 矩阵计算
离散傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT)是离散傅里叶变换(DFT)的逆操作。对于长度为 N N N 的复数序列 X [ k ] X[k] X[k],其逆变换 x [ n ] x[n] x[n] 定义为:
x [ n ] = 1 N ∑ k = 0 N − 1 X [ k ] ⋅ exp ( i 2 π k n N ) x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \cdot \exp\left(i \frac{2 \pi k n}{N}\right) x[n]=N1∑k=0N−1X[k]⋅exp(iN2πkn)
你可以通过矩阵乘法表示这个计算。定义矩阵 F − 1 F^{-1} F−1 的元素为:
F j k − 1 = 1 N exp ( i 2 π j k N ) F_{jk}^{-1} = \frac{1}{N} \exp\left(i \frac{2 \pi j k}{N}\right) Fjk−1=N1exp(iN2πjk)
其中 0 ≤ j , k < N 0 \leq j, k < N 0≤j,k<N。
然后,IDFT 可以通过以下矩阵乘法得到:
x = F − 1 ⋅ X x = F^{-1} \cdot X x=F−1⋅X
例如,对于 N = 4 N = 4 N=4,逆变换矩阵为:
F − 1 = 1 4 [ 1 1 1 1 1 − i − 1 i 1 1 1 1 1 i − 1 − i ] F^{-1} = \frac{1}{4} \begin{bmatrix} 1 & 1 & 1 & 1\\ 1 & -i & -1 & i\\ 1 & 1 & 1 & 1\\ 1 & i & -1 & -i \end{bmatrix} F−1=41 11111−i1i1−11−11i1−i
这里的 i i i 是虚数单位,和之前一样。
你可以观察到逆变换矩阵与 DFT 矩阵之间的关系:逆变换矩阵实际上是 DFT 矩阵的共轭转置,并除以 N N N。
所以,如果你已经有了 DFT 矩阵 F F F,那么逆变换矩阵可以通过以下方式得到:
F − 1 = 1 N F ∗ F^{-1} = \frac{1}{N} F^* F−1=N1F∗
其中 F ∗ F^* F∗ 是 F F F 的共轭转置。
这种关系也意味着,如果你使用 Eigen 或类似的库,你可以通过现有的 DFT 矩阵非常容易地计算逆变换矩阵。
代码实现:
#include 共轭矩阵和逆矩阵
共轭矩阵
给定一个复数矩阵 A A A,其共轭矩阵 A ˉ \bar{A} Aˉ 是将 A A A 中每个元素的实部不变,虚部取反得到的矩阵。如果 A A A 的元素表示为 a + b i a + bi a+bi,那么 A ˉ \bar{A} Aˉ 的对应元素为 a − b i a - bi a−bi。
逆矩阵
给定一个可逆的方阵 A A A,其逆矩阵 A − 1 A^{-1} A−1 满足以下条件:
A ⋅ A − 1 = A − 1 ⋅ A = I A \cdot A^{-1} = A^{-1} \cdot A = I A⋅A−1=A−1⋅A=I
其中 I I I 是单位矩阵。只有当 A A A 是方阵且其行列式不为零时,逆矩阵才存在。
共轭转置(Hermitian转置)
对于复数矩阵,还有一个与共轭和转置结合的操作称为共轭转置或Hermitian转置。给定复数矩阵 A A A,其共轭转置 A ∗ A^* A∗ 是首先取 A A A 的共轭,然后对结果进行转置。如果你有一个单位向量长度的傅里叶变换矩阵,其共轭转置将等于其逆矩阵。
代码演示:矩阵计算
#include 离散傅里叶变换 (2D DFT) 二维数据
离散傅里叶变换 (2D DFT)
二维傅里叶变换 - 直接计算
给定一个二维信号 f ( m , n ) f(m,n) f(m,n),其中 m = 0 , 1 , … , M − 1 m = 0, 1, \ldots, M-1 m=0,1,…,M−1 和 n = 0 , 1 , … , N − 1 n = 0, 1, \ldots, N-1 n=0,1,…,N−1,其二维离散傅里叶变换(2D DFT)定义为:
F ( u , v ) = ∑ m = 0 M − 1 ∑ n = 0 N − 1 f ( m , n ) ⋅ e − i 2 π ( u m M + v n N ) F(u,v) = \sum_{m=0}^{M-1}\sum_{n=0}^{N-1} f(m,n) \cdot e^{-i2\pi\left(\frac{um}{M} + \frac{vn}{N}\right)} F(u,v)=∑m=0M−1∑n=0N−1f(m,n)⋅e−i2π(Mum+Nvn)
其中, F ( u , v ) F(u, v) F(u,v) 是频率域信号, M M M 和 N N N 是图像的行和列的数量, i i i 是虚数单位。
代码实现:
// 二维傅里叶变换 - 直接计算
void FourierTransform2D(const std::vector<std::vector<double>> &image,
std::vector<std::vector<std::complex<double>>> &result) {
int M = image.size();
int N = image[0].size();
result.resize(M, std::vector<std::complex<double>>(N));
for (int u = 0; u < M; ++u) {
for (int v = 0; v < N; ++v) {
std::complex<double> sum(0, 0);
for (int x = 0; x < M; ++x) {
for (int y = 0; y < N; ++y) {
double exponent = -2 * M_PI * ((u * x / double(M)) + (v * y / double(N)));
std::complex<double> term(image[x][y], 0);
term *= std::exp(std::complex<double>(0, exponent));
sum += term;
}
}
result[u][v] = sum;
}
}
}
二维傅里叶变换 - 矩阵计算
上述2D DFT可以分解为两个独立的一维离散傅里叶变换。让我们仔细看一下这个过程:
- 首先,对每一行进行1D DFT:
对于每个固定的行 m m m,我们可以将列 n n n 上的1D信号进行傅里叶变换。设 g ( m , v ) g(m,v) g(m,v) 是该中间结果:
g ( m , v ) = ∑ n = 0 N − 1 f ( m , n ) ⋅ e − i 2 π v n N g(m,v) = \sum_{n=0}^{N-1} f(m,n) \cdot e^{-i2\pi\frac{vn}{N}} g(m,v)=∑n=0N−1f(m,n)⋅e−i2πNvn
- 然后,对每一列进行1D DFT:
对于上一步得到的每一列,我们可以在 m m m 方向上进行1D傅里叶变换。将 g ( m , v ) g(m,v) g(m,v) 带入前面的公式:
F ( u , v ) = ∑ m = 0 M − 1 g ( m , v ) ⋅ e − i 2 π u m M = ∑ m = 0 M − 1 ( ∑ n = 0 N − 1 f ( m , n ) ⋅ e − i 2 π v n N ) ⋅ e − i 2 π u m M F(u,v) = \sum_{m=0}^{M-1} g(m,v) \cdot e^{-i2\pi\frac{um}{M}} = \sum_{m=0}^{M-1} \left( \sum_{n=0}^{N-1} f(m,n) \cdot e^{-i2\pi\frac{vn}{N}} \right) \cdot e^{-i2\pi\frac{um}{M}} F(u,v)=∑m=0M−1g(m,v)⋅e−i2πMum=∑m=0M−1(∑n=0N−1f(m,n)⋅e−i2πNvn)⋅e−i2πMum
这就完成了2D DFT的计算。
代码实现:
// 离散傅里叶矩阵
Eigen::MatrixXcd DFTMatrix(int N) {
Eigen::MatrixXcd F(N, N);
std::complex<double> w = std::exp(std::complex<double>(0, -2 * M_PI / N));
for (int j = 0; j < N; ++j) {
for (int k = 0; k < N; ++k) {
F(j, k) = std::pow(w, j * k);
}
}
return F;
}
// 一维离散傅里叶变换
Eigen::VectorXcd DFT(const Eigen::VectorXcd& x) {
int N = x.size();
// 构建傅里叶矩阵
Eigen::MatrixXcd F = DFTMatrix(N); // 使用共轭转置并除以N
// 计算 DFT
Eigen::VectorXcd X = F * x;
return X;
}
// 离散傅里叶变换 - 二维
Eigen::MatrixXcd DFT2D(const Eigen::MatrixXd& image) {
int rows = image.rows();
int cols = image.cols();
Eigen::MatrixXcd result(rows, cols);
for (int i = 0; i < rows; i++) {
Eigen::VectorXd temp = image.row(i).transpose();
result.row(i) = DFT(temp);
}
for (int j = 0; j < cols; j++) {
Eigen::VectorXcd temp = result.col(j);
result.col(j) = DFT(temp);
}
return result;
}
二维离散傅里叶逆变换(2D IDFT)
二维傅里叶逆变换 - 直接计算
给定一个二维频域信号 F ( u , v ) F(u,v) F(u,v),其中 u = 0 , 1 , … , M − 1 u = 0, 1, \ldots, M-1 u=0,1,…,M−1 和 v = 0 , 1 , … , N − 1 v = 0, 1, \ldots, N-1 v=0,1,…,N−1,其二维离散傅里叶逆变换定义为:
f ( m , n ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 F ( u , v ) ⋅ e i 2 π ( u m M + v n N ) f(m,n) = \frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1} F(u,v) \cdot e^{i2\pi\left(\frac{um}{M} + \frac{vn}{N}\right)} f(m,n)=MN1∑u=0M−1∑v=0N−1F(u,v)⋅ei2π(Mum+Nvn)
代码实现:
// 二维傅里叶逆变换
void InverseFourierTransform2D(const std::vector<std::vector<std::complex<double>>> &transformed,
std::vector<std::vector<double>> &result) {
int M = transformed.size();
int N = transformed[0].size();
result.resize(M, std::vector<double>(N));
for (int x = 0; x < M; ++x) {
for (int y = 0; y < N; ++y) {
std::complex<double> sum(0, 0);
for (int u = 0; u < M; ++u) {
for (int v = 0; v < N; ++v) {
double exponent = 2 * M_PI * ((u * x / double(M)) + (v * y / double(N)));
std::complex<double> term = transformed[u][v] * std::exp(std::complex<double>(0, exponent));
sum += term;
}
}
result[x][y] = (sum.real() / (M * N));
}
}
}
二维傅里叶逆变换 - 矩阵计算
分解为两个一维离散傅里叶逆变换
- 首先,对每一行进行1D IDFT:
对于每个固定的行 u u u,我们可以将列 v v v 上的1D信号进行傅里叶逆变换。设 G ( u , n ) G(u,n) G(u,n) 是该中间结果:
G ( u , n ) = 1 N ∑ v = 0 N − 1 F ( u , v ) ⋅ e i 2 π v n N G(u,n) = \frac{1}{N}\sum_{v=0}^{N-1} F(u,v) \cdot e^{i2\pi\frac{vn}{N}} G(u,n)=N1∑v=0N−1F(u,v)⋅ei2πNvn
- 然后,对每一列进行1D IDFT:
对于上一步得到的每一列,我们可以在 u u u 方向上进行1D傅里叶逆变换:
f ( m , n ) = 1 M ∑ u = 0 M − 1 G ( u , n ) ⋅ e i 2 π u m M = 1 M N ∑ u = 0 M − 1 ( ∑ v = 0 N − 1 F ( u , v ) ⋅ e i 2 π v n N ) ⋅ e i 2 π u m M f(m,n) = \frac{1}{M}\sum_{u=0}^{M-1} G(u,n) \cdot e^{i2\pi\frac{um}{M}} = \frac{1}{MN}\sum_{u=0}^{M-1} \left( \sum_{v=0}^{N-1} F(u,v) \cdot e^{i2\pi\frac{vn}{N}} \right) \cdot e^{i2\pi\frac{um}{M}} f(m,n)=M1∑u=0M−1G(u,n)⋅ei2πMum=MN1∑u=0M−1(∑v=0N−1F(u,v)⋅ei2πNvn)⋅ei2πMum
总结:把2维 傅里叶变换 分解为1维 傅里叶变换,利用矩阵可以快速的计算。
// 离散傅里叶矩阵
Eigen::MatrixXcd DFTMatrix(int N) {
Eigen::MatrixXcd F(N, N);
std::complex<double> w = std::exp(std::complex<double>(0, -2 * M_PI / N));
for (int j = 0; j < N; ++j) {
for (int k = 0; k < N; ++k) {
F(j, k) = std::pow(w, j * k);
}
}
return F;
}
// 离散傅里叶逆变换 - 一维
Eigen::VectorXcd IDFT(const Eigen::VectorXcd& X) {
int N = X.size();
Eigen::MatrixXcd F_inv = DFTMatrix(N).adjoint() / N; // 使用共轭转置并除以N
// 计算 IDFT
Eigen::VectorXcd x = F_inv * X;
return x;
}
// 离散傅里叶逆变换 - 二维
Eigen::MatrixXcd IDFT2D(const Eigen::MatrixXcd& F) {
int rows = F.rows();
int cols = F.cols();
Eigen::MatrixXcd result = F;
for (int i = 0; i < rows; i++) {
Eigen::VectorXcd temp = result.row(i).transpose();
result.row(i) = IDFT(temp);
}
for (int j = 0; j < cols; j++) {
Eigen::VectorXcd temp = result.col(j);
result.col(j) = IDFT(temp);
}
return result;
}
幅度谱(振幅谱)和相位谱
在傅里叶变换中,可以将一个图像的频率信息分为两部分:幅度谱(振幅谱)和相位谱。
-
幅度谱(振幅谱): 描述了各个频率分量的大小或强度。对于二维离散傅里叶变换,幅度谱可以通过以下公式计算:
A ( u , v ) = ∣ F ( u , v ) ∣ = ℜ ( F ( u , v ) ) 2 + ℑ ( F ( u , v ) ) 2 A(u, v) = \left| F(u, v) \right| = \sqrt{{\Re{(F(u, v))}}^2 + {\Im{(F(u, v))}}^2} A(u,v)=∣F(u,v)∣=ℜ(F(u,v))2+ℑ(F(u,v))2
其中, F ( u , v ) F(u, v) F(u,v) 是频率域信号, ℜ \Re ℜ 和 ℑ \Im ℑ 分别表示复数的实部和虚部。
幅度谱反映了各个频率分量对图像整体结构的贡献大小。通常,低频分量包含了图像的主要信息,高频分量包含了边缘和细节信息。
-
相位谱: 描述了各个频率分量的相对时相,即各个正弦波在空间中的偏移。相位谱可以通过以下公式计算:
ϕ ( u , v ) = arctan ( ℑ ( F ( u , v ) ) ℜ ( F ( u , v ) ) ) \phi(u, v) = \arctan \left( \frac{\Im{(F(u, v))}}{\Re{(F(u, v))}} \right) ϕ(u,v)=arctan(ℜ(F(u,v))ℑ(F(u,v)))
其中, ϕ ( u , v ) \phi(u, v) ϕ(u,v) 是相位谱, ℑ \Im ℑ 和 ℜ \Re ℜ 分别表示复数的虚部和实部。
相位谱包含了图像的空间结构信息。即使在丢失了幅度谱的情况下,仅通过相位谱也可以大致重建出图像的结构。
-
重新构建频率域图像: 使用幅度谱和相位谱重新构建复数频率域图像:
F ′ ( u , v ) = A ( u , v ) ⋅ e i ϕ ( u , v ) F'(u, v) = A(u, v) \cdot e^{i\phi(u, v)} F′(u,v)=A(u,v)⋅eiϕ(u,v)
-
执行二维傅里叶逆变换: 使用 F ′ ( u , v ) F'(u, v) F′(u,v) 计算逆傅里叶变换以得到复原的空间域图像:
f ′ ( x , y ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 F ′ ( u , v ) ⋅ e i 2 π ( u x M + v y N ) f'(x, y) = \frac{1}{MN} \sum_{u=0}^{M-1}\sum_{v=0}^{N-1} F'(u, v) \cdot e^{i 2\pi\left(\frac{ux}{M} + \frac{vy}{N}\right)} f′(x,y)=MN1∑u=0M−1∑v=0N−1F′(u,v)⋅ei2π(Mux+Nvy)
其中, M M M 和 N N N 是图像的行和列的数量。
重要的是,这个过程假设你没有改变幅度谱和相位谱。如果你不修改这些谱线,逆变换将完全恢复原始图像。如果你在频率域中进行了修改,逆变换将反映这些更改。
代码实现:
// 从复数矩阵中获取幅度谱和相位谱
void getAmplitudeAndPhaseSpectra(const Eigen::MatrixXcd& data, Eigen::MatrixXd& amplitude, Eigen::MatrixXd& phase) {
int rows = data.rows();
int cols = data.cols();
amplitude.resize(rows, cols);
phase.resize(rows, cols);
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
amplitude(i, j) = std::abs(data(i, j)); // 幅度
phase(i, j) = std::arg(data(i, j)); // 相位
}
}
}
// 从幅度谱和相位谱重构复数矩阵
void reconstructFromAmplitudeAndPhase(const Eigen::MatrixXd& amplitude,
const Eigen::MatrixXd& phase,
Eigen::MatrixXcd& data) {
int rows = amplitude.rows();
int cols = amplitude.cols();
data.resize(rows, cols);
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
double a = amplitude(i, j);
double p = phase(i, j);
data(i, j) = std::polar(a, p); // 极坐标形式重构复数
}
}
}
//
/
//矩阵计算
// 从复数矩阵中获取幅度谱和相位谱
void getAmplitudeAndPhaseSpectra(const Eigen::MatrixXcd& data, Eigen::MatrixXd& amplitude, Eigen::MatrixXd& phase)
{
amplitude = data.array().abs().matrix();
phase = data.array().arg().matrix();
}
// 从幅度谱和相位谱重构复数矩阵
void reconstructFromAmplitudeAndPhase(const Eigen::MatrixXd& amplitude,
const Eigen::MatrixXd& phase,
Eigen::MatrixXcd& data)
{
data = (amplitude.array() * (phase.array().cos() + std::complex<double>(0, 1) * phase.array().sin())).matrix();
}
振幅谱移动到中心
二维离散傅里叶变换之前 操作实现
在二维离散傅里叶变换中,如果你不对图像进行任何预处理,直接对其进行傅里叶变换,你会发现低频分量位于图像的四个角落,而高频分量位于图像的中心。
这样的分布通常不方便观察和分析,因为在大多数情况下,我们关心的主要是低频分量。因此,通常在进行二维离散傅里叶变换之前,会对图像的每一个像素进行乘以 ( − 1 ) x + y (-1)^{x+y} (−1)x+y的预处理操作。这个操作可以将低频分量移至图像的中心,高频分量移至四周,从而更方便我们观察和分析。
总的来说,傅里叶变换中低频在四周,高频在中间的现象,与二维离散傅里叶变换处理图像时的特点有关,以及是否对图像进行了预处理操作。如果没有预处理,低频将出现在四个角落;如果进行了预处理,低频将出现在中心。
x+y如果是偶数, ( − 1 ) x + y (-1)^{x+y} (−1)x+y的值是1,否则它的值是-1。
代码实现:
// **图像进行-1幂操作**:然后经过fft变换后,低频会在振幅谱中间
Eigen::MatrixXd imageShift(const Eigen::MatrixXd &image)
{
int M = image.rows();
int N = image.cols();
Eigen::MatrixXd F_shifted(M, N);
// 通过乘以 (-1)^(u+v) 来平移频率
for (int u = 0; u < M; ++u)
{
for (int v = 0; v < N; ++v)
{
//(u + v) & 1 通过位的判断末尾如果是1 为奇数,为0,为偶数。 -1的奇次幂还是-1,偶次幂为1.
F_shifted(u, v) = image(u, v) * ((u + v) & 1 ? -1 : 1);
}
}
return F_shifted;
}
二维离散傅里叶变换之后 操作实现
在二维离散傅里叶变换中,如果你不对图像进行任何预处理,直接对其进行傅里叶变换,你会发现低频分量位于图像的四个角落,而高频分量位于图像的中心。
则 fftshift 会将 fft变换后的振幅谱 的第一象限与第三象限交换,将第二象限与第四象限交换,实现将四个角的低频移动到中心的位置。
代码实现:
// **振幅谱低频移动到中心(频率平移)**:方便操作,利用象限对称互换
Eigen::MatrixXd fftShift(const Eigen::MatrixXd &F)
{
int M = F.rows();
int N = F.cols();
Eigen::MatrixXd F_shifted(M, N);
int mid_M = M>>1;
int mid_N = N>>1;
// 交换第一象限和第三象限
F_shifted.block(0, 0, mid_M, mid_N) = F.block(mid_M, mid_N,mid_M,mid_N);
F_shifted.block(mid_M, mid_N,mid_M,mid_N) = F.block(0, 0, mid_M, mid_N);
// 交换第二象限和第四象限
F_shifted.block(0, mid_N,mid_M,mid_N) = F.block(mid_M, 0, mid_M, mid_N);
F_shifted.block(mid_M, 0, mid_M, mid_N) = F.block(0, mid_N,mid_M,mid_N);
return F_shifted;
}
增强振幅谱显示效果(方便观测)
1. 对数缩放
对数缩放可以用以下数学表达式表示:
A ′ ( u , v ) = log ( A ( u , v ) + 1 ) A'(u, v) = \log(A(u, v) + 1) A′(u,v)=log(A(u,v)+1)
其中 A ( u , v ) A(u, v) A(u,v) 是原始振幅谱, A ′ ( u , v ) A'(u, v) A′(u,v) 是对数缩放后的振幅谱。
代码实现:
// 对数幅度缩放
Eigen::MatrixXd logAmplitudeSpectrum(const Eigen::MatrixXd& spectrum) {
return (spectrum.array() + 1).log();
}
2. 幂律缩放
幂律缩放可以用以下数学表达式表示:
A ′ ( u , v ) = A ( u , v ) γ A'(u, v) = A(u, v)^\gamma A′(u,v)=A(u,v)γ
其中 γ \gamma γ 是幂律缩放的参数, A ( u , v ) A(u, v) A(u,v) 是原始振幅谱, A ′ ( u , v ) A'(u, v) A′(u,v) 是幂律缩放后的振幅谱。
代码实现:
// 乘幂尺度变换
Eigen::MatrixXd powerLawScaling(const Eigen::MatrixXd& spectrum, double gamma) {
return spectrum.array().pow(gamma);
}
3. 归一化
归一化可以用以下数学表达式表示:
A ′ ( u , v ) = A ( u , v ) − min ( A ) max ( A ) − min ( A ) A'(u, v) = \frac{{A(u, v) - \min(A)}}{{\max(A) - \min(A)}} A′(u,v)=max(A)−min(A)A(u,v)−min(A)
其中 min ( A ) \min(A) min(A) 和 max ( A ) \max(A) max(A) 分别是原始振幅谱 A ( u , v ) A(u, v) A(u,v) 的最小值和最大值, A ′ ( u , v ) A'(u, v) A′(u,v) 是归一化后的振幅谱。
代码实现:
// 归一化 to [0, 1]
Eigen::MatrixXd normalize(const Eigen::MatrixXd& spectrum) {
double minVal = spectrum.minCoeff();
double maxVal = spectrum.maxCoeff();
return (spectrum.array() - minVal) / (maxVal - minVal);
}
整合在一起
将这三个步骤结合在一起,振幅谱的增强可以表示为:
A ′ ( u , v ) = ( log ( A ( u , v ) + 1 ) ) γ − min ( log ( A + 1 ) ) γ max ( log ( A + 1 ) ) γ − min ( log ( A + 1 ) ) γ A'(u, v) = \frac{{\left( \log(A(u, v) + 1) \right)^\gamma - \min\left( \log(A + 1) \right)^\gamma}}{{\max\left( \log(A + 1) \right)^\gamma - \min\left( \log(A + 1) \right)^\gamma}} A′(u,v)=max(log(A+1))γ−min(log(A+1))γ(log(A(u,v)+1))γ−min(log(A+1))γ
其中 A ( u , v ) A(u, v) A(u,v) 是原始振幅谱, A ′ ( u , v ) A'(u, v) A′(u,v) 是增强后的振幅谱, γ \gamma γ 是幂律缩放的参数。
代码实现:
// 对数幅度缩放
Eigen::MatrixXd logAmplitudeSpectrum(const Eigen::MatrixXd& spectrum) {
return (spectrum.array() + 1).log();
}
// 乘幂尺度变换
Eigen::MatrixXd powerLawScaling(const Eigen::MatrixXd& spectrum, double gamma) {
return spectrum.array().pow(gamma);
}
// 归一化 to [0, 1]
Eigen::MatrixXd normalize(const Eigen::MatrixXd& spectrum) {
double minVal = spectrum.minCoeff();
double maxVal = spectrum.maxCoeff();
return (spectrum.array() - minVal) / (maxVal - minVal);
}
// 增强频谱显示
Eigen::MatrixXd enhanceSpectrumDisplay(const Eigen::MatrixXd& spectrum, double gamma=1) {
Eigen::MatrixXd logSpectrum = logAmplitudeSpectrum(spectrum);
Eigen::MatrixXd powerScaledSpectrum = powerLawScaling(logSpectrum, gamma);
return normalize(powerScaledSpectrum);
}
离散快速傅里叶变换(FFT)
当然,我们可以深入了解快速傅里叶变换(Fast Fourier Transform,简称FFT)的细节。
-
基本概念
FFT是离散傅里叶变换(DFT)的一种高效实现方式。DFT可以将一个长度为 N N N的离散时间序列转换为一个长度相同的频域序列。与直接计算DFT的复杂度为 O ( N 2 ) O(N^2) O(N2)相比,FFT的计算复杂度为 O ( N log N ) O(N \log N) O(NlogN)。 -
库利-图基(Cooley-Tukey)算法
库利-图基算法可能是最常用的FFT算法,它使用了分治策略。假设我们要计算长度为 N N


