C#数据结构学习笔记之二叉树实现及遍历
一、树的定义
树(Tree)是 n(n≥0)个相同类型的数据元素的有限集合。树中的数据元素叫结点(Node)。n=0 的树称为空树(Empty Tree);对于 n>0 的任意非空树 T 有:
(1)有且仅有一个特殊的结点称为树的根(Root)结点,根没有前驱结点;
(2)若n>1,则除根结点外,其余结点被分成了m(m>0)个互不相交的集合
T1,T2,…,Tm,其中每一个集合Ti(1≤i≤m)本身又是一棵树。树T1,T2,…,Tm
称为这棵树的子树(Subtree)。
由树的定义可知,树的定义是递归的,用树来定义树。因此,树(以及二叉
树)的许多算法都使用了递归。
树的形式定义为:树(Tree)简记为 T,是一个二元组,
T = (D, R)
其中:D是结点的有限集合;
R是结点之间关系的有限集合。
二、树的相关术语:
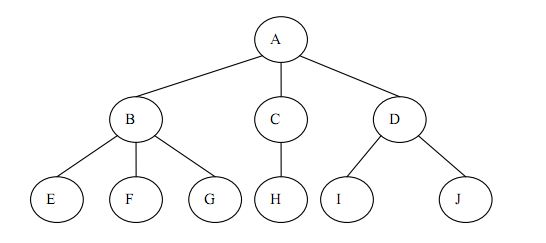
1、结点(Node):表示树中的数据元素,由数据项和数据元素之间的关系组
成。在图 5.1 中,共有 10 个结点。
2、结点的度(Degree of Node):结点所拥有的子树的个数,在图 5.1 中,结
点 A的度为3。
3、树的度(Degree of Tree):树中各结点度的最大值。在图 5.1 中,树的度为
3。
4、叶子结点(Leaf Node):度为 0 的结点,也叫终端结点。在图 5.1 中,结
点 E、F、G、H、I、J 都是叶子结点。
5、分支结点(Branch Node):度不为 0 的结点,也叫非终端结点或内部结点。
在图 5.1 中,结点 A、B、C、D 是分支结点。
6、孩子(Child):结点子树的根。在图 5.1 中,结点 B、C、D 是结点 A 的
孩子。
7、双亲(Parent):结点的上层结点叫该结点的双亲。在图 5.1 中,结点 B、C、
D的双亲是结点A。
8、祖先(Ancestor):从根到该结点所经分支上的所有结点。在图 5.1 中,结
点 E的祖先是 A和 B。
9、子孙(Descendant):以某结点为根的子树中的任一结点。在图 5.1 中,除
A之外的所有结点都是A的子孙。
10、兄弟(Brother):同一双亲的孩子。在图 5.1 中,结点 B、C、D互为兄弟。
11、结点的层次(Level of Node):从根结点到树中某结点所经路径上的分支
数称为该结点的层次。根结点的层次规定为1,其余结点的层次等于其双亲结点的层次加 1。
12、堂兄弟(Sibling):同一层的双亲不同的结点。在图 5.1 中,G 和 H 互为
堂兄弟。
13、树的深度(Depth of Tree):树中结点的最大层次数。在图 5.1 中,树的深
度为 3。
14、无序树(Unordered Tree):树中任意一个结点的各孩子结点之间的次序构
成无关紧要的树。通常树指无序树。
15、有序树(Ordered Tree):树中任意一个结点的各孩子结点有严格排列次序
的树。二叉树是有序树,因为二叉树中每个孩子结点都确切定义为是该结点的左
孩子结点还是右孩子结点。
16、森林(Forest):m(m≥0)棵树的集合。自然界中的树和森林的概念差别很
大,但在数据结构中树和森林的概念差别很小。从定义可知,一棵树有根结点和
m 个子树构成,若把树的根结点删除,则树变成了包含 m 棵树的森林。当然,根
据定义,一棵树也可以称为森林。
三、树的根本操作
1、Root():求树的根结点,如果树非空,返回根结点,否则返回空;
2、Parent(t):求结点 t的双亲结点。如果 t 的双亲结点存在,返回双亲结点,
否则返回空;
3、Child(t,i):求结点 t 的第 i 个子结点。如果存在,返回第 i 个子结点,否
则返回空;
4、RightSibling(t):求结点 t 第一个右边兄弟结点。如果存在,返回第一个
右边兄弟结点,否则返回空;
5、Insert(s,t,i):把树 s插入到树中作为结点 t 的第 i 棵子树。成功返回 true,
否则返回 false;
6、Delete(t,i):删除结点t 的第i棵子树。成功返回第i 棵子树的根结点,否
则返回空;
7、Traverse(TraverseType):按某种方式遍历树;
8、Clear():清空树;
9、IsEmpty():判断树是否为空树。如果是空树,返回 true,否则返回false;
10、GetDepth():求树的深度。如果树不为空,返回树的层次,否则返回0。
四、二叉树的定义
- 二叉树(Binary Tree)是n(n≥0)个相同类型的结点的有限集合。n=0 的二叉树
称为空二叉树(Empty Binary Tree);对于 n>0 的任意非空二叉树有:
(1)有且仅有一个特殊的结点称为二叉树的根(Root)结点,根没有前驱结
点;
(2)若n>1,则除根结点外,其余结点被分成了 2 个互不相交的集合TL,
TR,而TL、TR本身又是一棵二叉树,分别称为这棵二叉树的左子树(Left Subtree)
和右子树(Right Subtree)。
二叉树的形式定义为:二叉树(Binary Tree)简记为 BT,是一个二元组,
BT = (D, R)
其中:D是结点的有限集合;
R是结点之间关系的有限集合。
由树的定义可知,二叉树是另外一种树形结构,并且是有序树,它的左子树
和右子树有严格的次序,若将其左、右子树颠倒,就成为另外一棵不同的二叉树。
- 二叉树的形态共有 5 种:空二叉树、只有根结点的二叉树、右子树为空的二
叉树、左子树为空的二叉树和左、右子树非空的二叉树。
- 满二叉树(Full Binary Tree):如果一棵二叉树只有度为 0 的结点和度为 2
的结点,并且度为 0 的结点在同一层上,则这棵二叉树为满二叉树,如图 5.7(a)
所示。 由定义可知,对于深度为k的满二叉树的结点个数为 2k-1。
- 完全二叉树(Complete Binary Tree):深度为 k,有 n 个结点的二叉树当且仅当其每一个结点都与深度为 k,有 n 个结点的满二叉树中编号从1到n的结点一一对应时,称为完全二叉树,如图 5.7(b)所示。 完全二叉树的特点是叶子结点只可能出现在层次最大的两层上,并且某个结点的左分支下子孙的最大层次与右分支下子孙的最大层次相等或大 1。

- 二叉树的遍历:
a) 二叉树的遍历是指按照某种顺序访问二叉树中的每个结点,使每个结点被访
问一次且仅一次。遍历是二叉树中经常要进行的一种操作,因为在实际应用中,
常常要求对二叉树中某个或某些特定的结点进行处理,这需要先查找到这个或这
些结点。
b) 实际上,遍历是将二叉树中的结点信息由非线性排列变为某种意义上的线性
排列。也就是说,遍历操作使非线性结构线性化。
c) 由二叉树的定义可知,一棵二叉树由根结点、左子树和右子树三部分组成,
若规定 D、L、R 分别代表遍历根结点、遍历左子树、遍历右子树,则二叉树的
遍历方式有6 种:DLR、DRL、LDR、LRD、RDL、RLD。由于先遍历左子树和
先遍历右子树在算法设计上没有本质区别,所以,只讨论三种方式:DLR(先序
遍历)、LDR(中序遍历)和 LRD(后序遍历)。
d) 除了这三种遍历方式外,还有一种方式:层序遍历(Level Order)。层序遍历
是从根结点开始,按照从上到下、从左到右的顺序依次访问每个结点一次仅一次。
由于树的定义是递归的,所以遍历算法也采用递归实现。下面分别介绍这四
种算法
e) 先序遍历的基本思想是:首先访问根结点,然后先序遍历其左子树,最后先序遍历其右子树。
f) 中序遍历的基本思想是:首先中序遍历根结点的左子树,然后访问根结点,最后中序遍历其右子树。
g) 后序遍历的基本思想是:首先后序遍历根结点的左子树,然后后序遍历根结点的右子树,最后访问根结点。
h) 层序遍历的基本思想是:由于层序遍历结点的顺序是先遇到的结点先访问,队列操作的顺序相同。所以,在进行层序遍历时,设置一个队列,将根结点引入队,当队列非空时,循环执行以下三步:
(1) 从队列中取出一个结点引用,并访问该结点;
(2) 若该结点的左子树非空,将该结点的左子树引用入队;
(3) 若该结点的右子树非空,将该结点的右子树引用入队;
- 6. 二叉树实现的具体代码(包括二叉树类的建立及先序、中序、后序算法的具体实现代码):
using System;
using System.Collections.Generic;
using System.Collections;
class Program
{
static void
{
Node<string> H = new Node<string>("H",null,null);
Node<string> I = new Node<string>("I",null,null);
Node<string> J = new Node<string>("J",null,null);
Node<string> D = new Node<string>("D",H,I);
Node<string> E = new Node<string>("E", J,null);
Node<string> B = new Node<string>("B", D, E);
Node<string> F = new Node<string>("F", null, null);
Node<string> G = new Node<string>("G", null, null);
Node<string> C = new Node<string>("C", F, G);
Node<string> A = new Node<string>("A", B, C);
Console.WriteLine("先序遍历结果集:");
Node<string>.PreOrder(A);
Console.WriteLine("中序遍历结果集:");
Node<string>.InOrder(A);
Console.WriteLine("后序遍历结果集:");
Node<string>.PostnOrder(A);
Console.WriteLine("层序遍历结果集:");
Node<string>.LevelOrder(A);
}
}
//建立二叉树的泛型类
public class Node<T>
{
private T data; //数据域
private Node<T> lChild; //左孩子
private Node<T> rChild; //右孩子
//构造器
public Node(T val, Node<T> lp, Node<T> rp)
{
data = val;
lChild = lp;
rChild = rp;
}
//构造器
public Node(Node<T> lp, Node<T> rp)
{
data = default(T);
lChild = lp;
rChild = rp;
} //构造器
public Node(T val)
{
data = val;
lChild = null;
rChild = null;
}
//构造器
public Node()
{
data = default(T);
lChild = null;
rChild = null;
}
//数据属性
public T Data
{
get
{
return data;
}
set
{
value = data;
}
}
//左孩子属性
public Node<T> LChild
{
get
{
return lChild;
}
set
{ lChild = value;
}
}
//右孩子属性
public Node<T> RChild
{
get
{
return rChild;
}
set
{
rChild = value;
}
}
public static void PreOrder(Node<T> root)
{
//根结点为空
if (root == null)
{
return;
}
//处理根结点
Console.WriteLine("{0}", root.Data);
//先序遍历左子树
PreOrder(root.lChild);
//先序遍历右子树
PreOrder(root.rChild);
}
public static void InOrder(Node<T> root)
{
//根结点为空
if (root==null)
{
return;
}
//中序遍历左子树
InOrder(root.LChild);
Console.WriteLine("{0}", root.data);
//中序遍历右子树
InOrder(root.rChild);
}
public static void PostnOrder(Node<T> root)
{
//根结点为空
if (root == null)
{
return;
}
//后序遍历左子树
PostnOrder(root.LChild);
//后序遍历右子树
PostnOrder(root.rChild);
Console.WriteLine("{0}", root.data);
}
public static void LevelOrder(Node<T> root)
{
//根结点为空
if (root == null)
{
return;
}
//设置一个队列保存层序遍历的结点
CSeqQueue<Node<T>> sq = new CSeqQueue<Node<T>>(50);
//根结点入队
sq.In(root);
//队列非空,结点没有处理完
while (!sq.IsEmpty())
{
//结点出队
Node<T> tmp = sq.Out();
//处理当前结点
Console.WriteLine("{0}", tmp.data);
//将当前结点的左孩子结点入队
if (tmp.LChild != null)
{
sq.In(tmp.LChild);
}
//将当前结点的右孩子结点入队
if (tmp.RChild != null)
{
sq.In(tmp.RChild);
}
}
}
}
//Queue接口
public interface IQueue<T>
{
int GetLength(); //求队列的长度
bool IsEmpty(); //判断对列是否为空
void Clear(); //清空队列
void In(T item); //入队
T Out(); //出队
T GetFront(); //取对头元素
}
//Queue泛型实例
public class CSeqQueue<T> : IQueue<T> {
private int maxsize; //循环顺序队列的容量
private T[] data; //数组, 用于存储循环顺序队列中的数据元素
private int front; //指示循环顺序队列的队头
private int rear; //指示循环顺序队列的队尾
//索引器
public T this[int index]
{
get
{
return data[index];
}
set
{
data[index] = value;
}
}
//容量属性
public int Maxsize
{
get
{
return maxsize;
}
set
{
maxsize = value;
}
}
//队头属性
public int Front
{
get
{
return front;
}
set
{
front = value;
}
}
//队尾属性
public int Rear
{
get
{
return rear;
}
set
{
rear = value;
}
}
//构造器
public CSeqQueue(int size)
{
data = new T[size];
maxsize = size;
front = rear = -1;
}
//求循环顺序队列的长度
public int GetLength()
{
return (rear-front+maxsize) % maxsize;
}
//清空循环顺序队列
public void Clear()
{
front = rear = -1;
}
//判断循环顺序队列是否为空
public bool IsEmpty()
{
if (front == rear)
{
return true;
}
else
{
return false;
}
}
//判断循环顺序队列是否为满
public bool IsFull()
{
if ((rear + 1) % maxsize==front)
{
return true;
}
else
{
return false;
}
}
//入队
public void In(T item)
{
if(IsFull())
{
Console.WriteLine("Queue is full");
return;
}
data[++rear] = item;
}
//出队
public T Out()
{
T tmp = default(T);
if (IsEmpty())
{
Console.WriteLine("Queue is empty");
return tmp;
}
tmp = data[++front];
return tmp;
}
//获取队头数据元素
public T GetFront()
{
if (IsEmpty())
{
Console.WriteLine("Queue is empty!");
return default(T);
}
return data[front + 1];
}
- }树转换为二叉树
由于二叉树是有序的,为了避免混淆,对于无序树,我们约定树中的每个结
点的孩子结点按从左到右的顺序进行编号。如图5.1 所示的树,根结点 A有三个
孩子 B、C、D,规定结点 B 是结点 A 的第一个孩子,结点 C 是结点 A 的第 2
个孩子,结点 D是结点 A的第3个孩子。
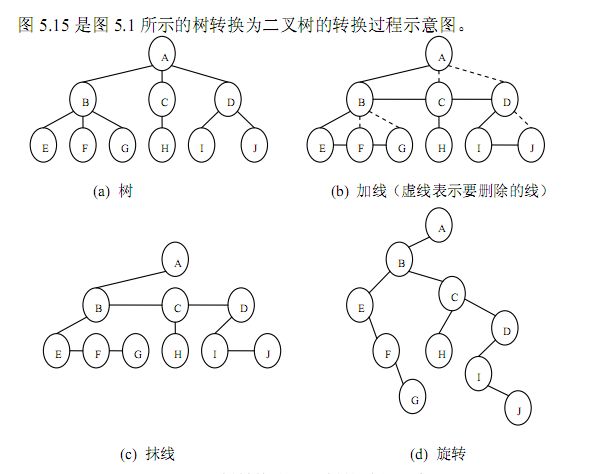
将树转换成二叉树的步骤是:
(1)加线。就是在所有兄弟结点之间加一条连线;
(2)抹线。就是对树中的每个结点,只保留他与第一个孩子结点之间的连
线,删除它与其它孩子结点之间的连线;
(3)旋转。就是以树的根结点为轴心,将整棵树顺时针旋转一定角度,使
之结构层次分明。
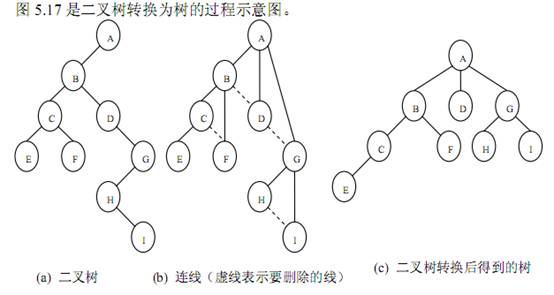
- 二叉树转换为树
二叉树转换为树是树转换为二叉树的逆过程,其步骤是:
(1)若某结点的左孩子结点存在,将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点,将该结点与这些右孩子结点用线连接起来;
(2)删除原二叉树中所有结点与其右孩子结点的连线;
(3)整理(1)和(2)两步得到的树,使之结构层次分明。
图 5.17 是二叉树转换为树的过程示意图。