深度学习基础篇 第一章:卷积
dummy老弟这几天在复习啊我也跟着他重新复习一轮。
这次打算学的细一点,虽然对工作没什么帮助,但是理论知识也能更扎实吧!
从0开始的深度学习大冒险。
参考教程:
https://www.zhihu.com/question/22298352
https://zhuanlan.zhihu.com/p/555957573?utm_id=0
https://zhuanlan.zhihu.com/p/394917827
文章目录
- 什么是卷积
-
- 卷积的数学意义
- 图像处理中的卷积
- 深度学习中的卷积
-
- 从全连接层说起
- 卷积的特性
-
- 稀疏连接
- 权值共享
- 其它特性
- 卷积的相关概念
-
- 卷积的三种模式
- 填充的四种形式
- 卷积的计算
-
- 感受野的计算
-
- 从下往上计算
- 从上往下计算
- 参数量和运算量的计算
- 代码实现
-
- 普通版本
- 优化版本
什么是卷积
卷积的数学意义
首先从数学公式的角度看一下卷积。
从公式来看,卷积有两种形式,一种是连续形式,一种是离散形式。
- 连续形式
( f ∗ g ) ( n ) = ∫ − ∞ ∞ f ( τ ) g ( n − τ ) d τ (f*g)(n) = \int^{\infty}_{-\infty}f(\tau)g(n-\tau)d\tau (f∗g)(n)=∫−∞∞f(τ)g(n−τ)dτ - 离散形式
( f ∗ g ) ( n ) = ∑ τ = − ∞ ∞ f ( τ ) g ( n − τ ) (f*g)(n) = \sum^{\infty}_{\tau=-\infty}f(\tau)g(n-\tau) (f∗g)(n)=τ=−∞∑∞f(τ)g(n−τ)
两种形式的公式的共通的部分是:
f ( τ ) g ( n − τ ) f(\tau)g(n-\tau) f(τ)g(n−τ)
f ( τ ) f(\tau) f(τ)是一个与 n n n无关的函数,它可以理解为某个点 τ \tau τ对应的一个系统结果,与别的因素无关。 g ( n − τ ) g(n-\tau) g(n−τ)衡量了两个点 n n n和 t a u tau tau之间的关系, f ( τ ) g ( n − τ ) f(\tau)g(n-\tau) f(τ)g(n−τ)可以理解成 τ \tau τ的结果对 n n n的影响。
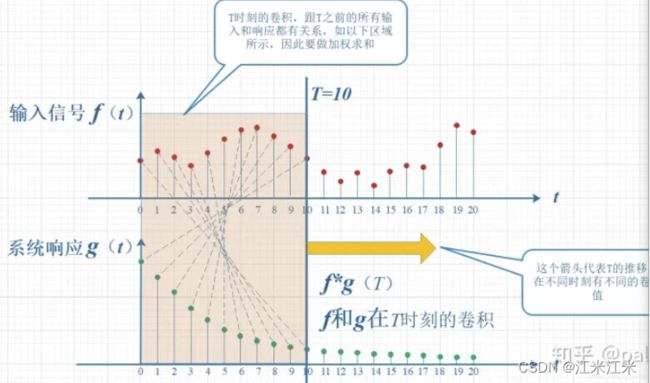
在连续形式中,做的是一个积分;在离散形式中,则是一个累加和。不管是什么形式,卷积公式都可以看成点 n n n受到的其它所有点 τ \tau τ的影响的累加。
在 n n n固定的情况下, τ \tau τ越大, n − τ n-\tau n−τ就越小。 τ \tau τ越小, n − τ n-\tau n−τ就越大。
在 n = 10 n=10 n=10的情况下, f ( τ ) f(\tau) f(τ)与 g ( 10 − τ ) g(10-\tau) g(10−τ)的对应关系如上图,在 τ = 0 \tau=0 τ=0时,要计算的是 f ( 0 ) g ( 10 ) f(0)g(10) f(0)g(10),在 τ = 10 \tau=10 τ=10时,要计算的是 f ( 10 ) g ( 0 ) f(10)g(0) f(10)g(0)。两者形成一个“卷”的关系,同时求周围所有点对当前点的影响,又需要“积”。整体组合成了一个“卷积”的计算。
图像处理中的卷积
这部分参考:https://www.zhihu.com/question/22298352/answer/228543288
我们的图像一般是二维图像【先不考虑通道数的情况】,我们对图像进行卷积处理,使用的就是二维卷积,用的函数,也是二元函数。
下面给出了一个平滑图像的例子。
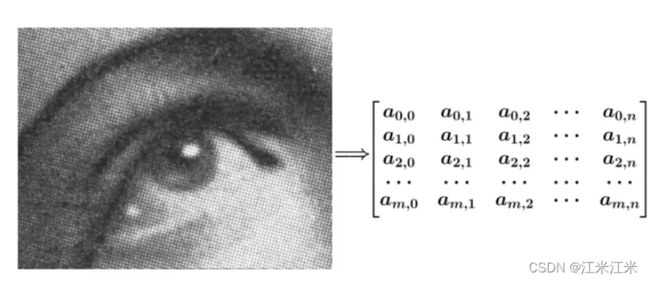
我们的图像是由多个像素点组成的,我们把它用函数表示为 f ( x , y ) = a x , y f(x,y) = a_{x,y} f(x,y)=ax,y。
同时我们用一个平均矩阵,作为我们的 g ( x , y ) = b x , y g(x,y) = b_{x,y} g(x,y)=bx,y,用这个矩阵对我们的图像进行卷积操作,来得到一个新的平滑的图像。【这个矩阵在这里其实就是我们常说的卷积核】

我们可以看到矩阵g中元素的下标取值范围和预想的有点不一样,考虑到一维情况下在进行计算时使用的是 g ( n − τ ) g(n-\tau) g(n−τ),在二维情况下,我们使用的是 g ( u − i , v − j ) g(u-i,v-j) g(u−i,v−j),以 u , v u,v u,v为中心向外辐射再考虑周围的点,这个范围是【-1,1】,也就是中心点和它的八邻域。
写成公式后是
( f ∗ g ) ( u , v ) = ∑ i ∑ j f ( i , j ) g ( u − i , v − j ) = ∑ i ∑ j a i , j b u − i , v − j (f*g)(u,v) = \sum_i\sum_jf(i,j)g(u-i,v-j) = \sum_i\sum_ja_{i,j}b_{u-i,v-j} (f∗g)(u,v)=i∑j∑f(i,j)g(u−i,v−j)=i∑j∑ai,jbu−i,v−j
在这个公式中,i和j受到了g(u,v)函数和u,v取值的限制。
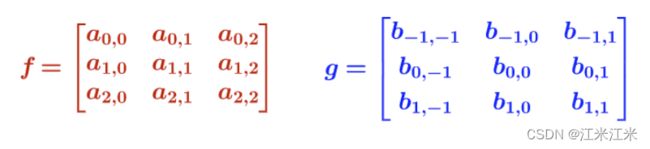
假如 u = 1 , v = 1 u=1,v=1 u=1,v=1,那么公式表示为:
( f ∗ g ) ( 1 , 1 ) = ∑ i = 0 2 ∑ j = 0 2 f ( i , j ) g ( 1 − i , 1 − j ) = a 0 , 0 b 1 , 1 + a 0 , 1 b 1 , 0 + a 0 , 2 b 1 , − 1 + a 1 , 0 b 0 , 1 + a 1 , 1 b 0 , 0 + a 1 , 2 b 0 , − 1 + a 2 , 0 b − 1 , 1 + a 2 , 1 b − 1 , 0 + a 2 , 2 b − 1 , − 1 \begin{align} (f*g)(1,1) &= \sum_{i=0}^2\sum_{j=0}^2f(i,j)g(1-i,1-j)\\ &=a_{0,0}b_{1,1}+a_{0,1}b_{1,0}+a_{0,2}b_{1,-1}+a_{1,0}b_{0,1}+a_{1,1}b_{0,0}\\ &+a_{1,2}b_{0,-1}+a_{2,0}b_{-1,1}+a_{2,1}b_{-1,0}+a_{2,2}b_{-1,-1} \end{align} (f∗g)(1,1)=i=0∑2j=0∑2f(i,j)g(1−i,1−j)=a0,0b1,1+a0,1b1,0+a0,2b1,−1+a1,0b0,1+a1,1b0,0+a1,2b0,−1+a2,0b−1,1+a2,1b−1,0+a2,2b−1,−1
在这个公式和配图的组合中我们能发现,位于左上角的 a 0 , 0 a_{0,0} a0,0与位于右下角的 b 1 , 1 b_{1,1} b1,1相乘,位于右下角的 a 2 , 2 a_{2,2} a2,2与位于左上角的 b − 1 , − 1 b_{-1,-1} b−1,−1相乘,它们之间也是又有“卷”又有“积”的操作。
随着 u , v u,v u,v的数值的改变,我们的矩阵g在图像上进行滑动求和,计算出新的数值,从而实现了对图像的卷积操作。一般在使用时,会对g矩阵旋转180°,这样计算起来比较方便。,也就是将g变为:
g = [ b 1 , 1 b 1 , 0 b 1 , − 1 b 0 , 1 b 0 , 0 b 0 , − 1 b − 1 , 1 b − 1 , 0 b − 1 , − 1 ] g = \begin{bmatrix}b_{1,1}&b_{1,0}&b_{1,-1}\\ b_{0,1}&b_{0,0}&b_{0,-1}\\ b_{-1,1}&b_{-1,0}&b_{-1,-1}\\ \end{bmatrix} g= b1,1b0,1b−1,1b1,0b0,0b−1,0b1,−1b0,−1b−1,−1
当前在深度学习中我们不用考虑这个翻转,直接计算就可以。
深度学习中的卷积
深度学习中的卷积,也称为滤波器。它由一组卷积核组成,这个卷积核就类似于在上一节中说到的矩阵g,它具有固定的大小,在输入图像上通过滑动求值。但是和我们使用的具有固定数值的矩阵g不同的是,深度学习中的卷积核的参数是可学习的,会随着训练的进行不断更新。
在深度学习中,我们输入一个多通道的特征图,使用特定数目的卷积核对特征图进行计算, 并得到一个拥有更高层语义信息的输出特征图。
从全连接层说起
一般我们都会进行卷积层核全连接层的对比,相比全连接层,卷积层有着自己的优势。
我们先从一张图看一下在处理二维图像时,全连接层存在什么问题。

对于一个大小为200x200的输入图像,我们使用全连接层对这个图像直接做分类任务,目标是1000分类。全连接,顾名思义,就是所有的节点都连接在一起,那么它的输入节点数目是200x200=40000,输出节点数目是1000,连接数是40000000,参数量也是如此。
如图中所说,它的参数量太多,计算量比较大。同时,对于200x200的图像,一般是进行flatten操作将其变为40000个节点,这个操作会使得图像的空间信息丢失,并且相邻像素点也会被分开处理。
概括来讲,全连接层的缺点是:
- 使用密集连接,计算量大,参数量也大。
- 丢失空间信息,空间结构被破坏。
卷积的特性
全连接层会丢失空间信息,但是卷积是在图像中某个点和它的邻域进行计算,空间结构不会被破坏,这是它的一个优点。另一个优点就是相对全连接层来说,它的计算量参数量都要小很多。
这主要依赖于它的两个特性:
- 稀疏连接。
- 权值共享。
稀疏连接
传统的全连接层使用矩阵乘法计算,每个输入核输出之间进行密集连接,所有的输入和输出单元都要进行交互。而卷积网络则使用的是稀疏连接,输出单元只和部分输入单元有交互,极大的减少了计算量。
如图中所示,假如你使用的卷积核大小为3x3,那么你的每个输出单元只需要和9个输入单元存在交互。

对于上图,你的输入大小是7x7,输出大小是5x5。假如使用全连接层进行计算,那么你的输入单元数是49,输出单元数是25,连接数是49x25 = 1225。
使用卷积层时,每个输出单元只需要和3x3个输入单元交互,所以连接数是25x9 = 225。相比于全连接层的连接数大大减少。
权值共享
在卷积层中,卷积核的参数是共享的。权值共享是指在计算图层输出时多次使用同样的参数进行运算。对于一个输入的图像,使用卷积核在上面进行滑动遍历,不管遍历多少次,参数的数量都是固定的。
在全连接层中,1225个连接就意味着有1225个权重参数要学习,而对于卷积层,使用一个大小为3x3的卷积核,就意味着要学习的参数有3x3+1(bias)=10个,相比于全连接层也是大大减少的。
其它特性
卷积层还有一些别的特性:
- 平移不变性
当图像中的目标发生偏移时,网络能输出一致的结果。这里主要针对的是分类的任务,对于图像中目标发生位置偏移,图像分类的结果应该保持一致。 - 平移等变性
当输入发生偏移时,网络的输出结果也有相应的偏移。这里主要针对的是目标检测等任务。
卷积的相关概念
- 卷积核(kernel):卷积基本组成单元,一般使用的卷积核大小为3x3或者5x5,卷积核通常是一个二维的概念。
- 滤波器(filter):滤波器和卷积核的概念可以互换,但是本质上略有不同,滤波器是多个卷积核堆叠的结果。如果使用的是二维的权重矩阵,那么滤波器和卷积核是等价的,假如是多维的情况下,使用滤波器这个表述更合适。
- 感受野(Receptive field):当前特征图上的像素点在原始图像上映射的区域大小。
- 步长(stride):卷积核在输入图像上进行滑动遍历时的步长。一般我们希望得到一个比输入图像尺寸要小的输出,可以通过控制步长来控制输出的大小。
- 填充(padding):对输入图像边界进行填充,可以改变输入特征图的大小。
卷积的三种模式
常用的卷积有三种模式:full,same,valid。这主要取决出卷积输出特征图的大小,影响输出特征图大小的因素只要有卷积核大小,步长和填充大小。
我们先给一个特征图大小的计算公式:
D o u t p u t = D i n p u t − D k e r n e l + 2 × P a d d i n g S t r i d e + 1 D_{output} = \frac{D_{input}-D_{kernel}+2\times Padding}{Stride}+1 Doutput=StrideDinput−Dkernel+2×Padding+1
假如输入特征图大小为5x5,使用大小为3x3的卷积核,步长为2,padding为0,那么直接得到的输出特征图大小为:
5 − 3 + 2 × 0 2 + 1 = 2 \frac{5-3+2\times0}{2}+1 = 2 25−3+2×0+1=2
- full卷积
full卷积是一种上采样卷积,它允许卷积核比特征图大。比如说输入是2x2的特征图,使用大小为3x3,步长为1的卷积后,输出大小为4x4的特征图。代入上面的公式,我们可以知道,这种情况下,padding的大小为2。
实际上,在这种情况下,使用的padding一般都为固定值,即 D k e r n e l − 1 D_{kernel}-1 Dkernel−1 - same卷积
same卷积是一种输出特征图和输入特征图大小保持一致的卷积方式。为了保持一致,通常需要你自己计算一下padding的大小。 - valie卷积
valid卷积是最常用的下采样卷积,它的特点是卷积核不能超过特征图的范围。在这种情况下,一般不使用padding。
填充的四种形式
边界填充手段有多种,常用的一般有四种。
- 零填充ZeroPad2d:使用值0进行边界填充。
- 常数填充ConstantPad2d:使用指定常数进行填充,零填充可以看作一种特殊的常数填充。
- 镜像填充ReflectionPad2d:使用中心对称的对边方向的值进行填充。
- 重复填充ReplicationPad2d:使用边缘像素值填充。【和edge填充应该是同一类】
此外还有一些别的方法,比如对称填充:以特征图边界为对称中心进行填充。
卷积的计算
感受野的计算
从下往上计算
我们按照从下往上的计算方法,从最后一层开始递推,传递到第一层。
感受野计算公式:
R F i = ( R F i + 1 − 1 ) × S t r i d e i + K s i z e i RF_i = (RF_{i+1}-1)\times Stride_i + K_{size_i} RFi=(RFi+1−1)×Stridei+Ksizei
这个公式其实是特征图大小正向计算倒推得到的,不考虑padding的大小。
假如我们现在在第5层,通过递推得到的 R F 0 RF_0 RF0的值,其实是第五层相对输入的感受野大小。理解上可能有些绕,用一个具体的例子看看。
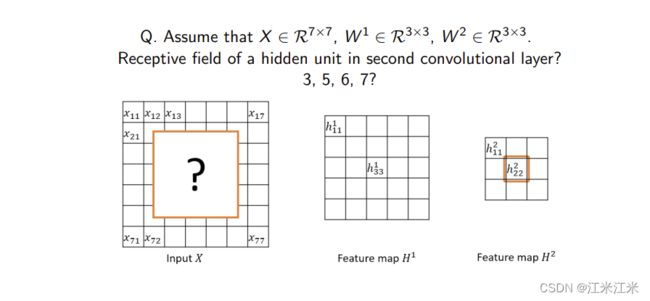
如上图,输入大小为7x7的特征图,经过两个3x3卷积后,求最后一层的感受野大小。
| Layer | kernel | Stride |
|---|---|---|
| input | ||
| conv1 | 3x3 | 1 |
| conv2 | 3x3 | 1 |
对于conv2:大小为3。
对于conv1:大小为 ( 3 − 1 ) × 1 + 3 = 5 (3-1)\times1+3=5 (3−1)×1+3=5
所以对于最后一层,感受野大小就是5。
从上往下计算
也可以从原始输入出发,逐层迭代到最后。
计算公式是:
R F i + 1 = ( K − 1 ) ∗ ∏ n = 0 i S n + R F i RF_{i+1} = (K-1)*\prod_{n=0}^iS_n + RF_i RFi+1=(K−1)∗n=0∏iSn+RFi
还是使用上面的例子:初始感受野为1。
| Layer | kernel | Stride | RF |
|---|---|---|---|
| input | 1 | ||
| conv1 | 3x3 | 1 | 2*1+1 = 3 |
| conv2 | 3x3 | 1 | 2*1+3 = 5 |
参数量和运算量的计算
在实际使用中,我们一般不会使用单个卷积核进行卷积计算,而是使用多个filter针对多维输入特征图进行运算,并输出一个新的多维特征图。
先给出公式,然后看例子。
对于卷积层,它的参数量计算公式如下:
p a r a m s = C o × ( k w × k h × C i + 1 ) params = C_o \times (k_w \times k_h \times C_i + 1) params=Co×(kw×kh×Ci+1)
对于卷积层,它的运算量计算公式如下:
F L O P s = C i × C o × k w × k h × W o × H o FLOPs = C_i \times C_o \times k_w \times k_h \times W_o \times H_o FLOPs=Ci×Co×kw×kh×Wo×Ho
我们一步一步来看一下参数量和计算量是怎么计算的。
- 一通道输入,多通道输出

图中给出的例子,输入是一个大小为7x7的特征图,输出为2x5x5的特征图。具体来说,在这一层中使用了2个大小为3x3的filter。(因为是二维filter,所以和kernel是等价的)
所以这一层的可学习参数量为 2 × ( 3 × 3 + 1 ) = 20 2\times(3\times3+1)=20 2×(3×3+1)=20。
这一层的连接数为 2 × ( 3 × 3 × 5 × 5 ) = 450 2\times(3\times3\times5\times5)=450 2×(3×3×5×5)=450。 - 多通道输入,一通道输出
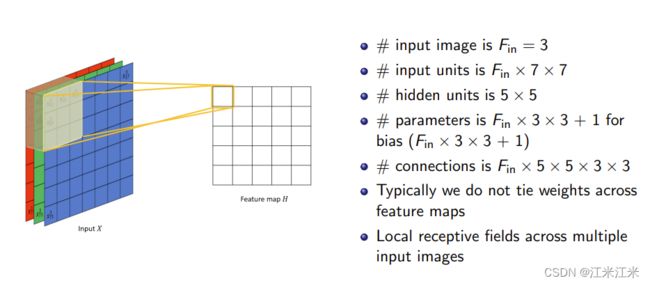
图中给出的例子,输入是一个大小为3x7x7的特征图,输出为5x5的特征图。具体来说,在这一层中使用了一个大小为3x3x3的filter。
所以这一层的可学习参数量为 3 × 3 × 3 + 1 3\times3\times3+1 3×3×3+1。
这一层的连接数为 3 × ( 3 × 3 × 5 × 5 ) = 675 3\times(3\times3\times5\times5) = 675 3×(3×3×5×5)=675。 - 多通道输入,多通道输出

图中给出的例子,输入是一个大小为3x7x7的特征图,输出为2x5x5的特征图。具体来说,在这一层中使用了2个大小为3x3x3的filter。
所以这一层的可学习参数量为 2 × ( 3 × 3 × 3 + 1 ) 2\times(3\times3\times3+1) 2×(3×3×3+1)。
这一层的连接数为 2 × 3 × ( 3 × 3 × 5 × 5 ) = 1350 2\times3\times(3\times3\times5\times5) = 1350 2×3×(3×3×5×5)=1350。
代码实现
下面给出两个版本的代码实现。
普通版本
下面没有考虑stride,可以自己修改一下
import numpy as np
class Conv:
def __init__(self,c_in, c_out,kernel):
self.c_in = c_in
self.c_out = c_out
self.kernel = kernel
self.filter_shape = (c_out, c_in, kernel, kernel)
self.filter = np.random.randn(*self.filter_shape)
def forward(self,img):
self.img = img
h, w, c = img.shape
out_h = h - self.kernel + 1
out_w = h - self.kernel + 1
output = np.zeros((out_h, out_w, self.c_out))
for i in range(out_h):
for j in range(out_w):
for m in range(self.c_out):
for n in range(self.c_in):
cur_img = img[i:i+ self.kernel,j:j+self.kernel,n]
output[i][j][m] += np.sum(np.multiply(cur_img, self.filter[m][n]))
return output
def backward(self, gradient):
kernel_grad = np.zeros(self.filter_shape)
h,w,c = gradient.shape
in_h = h - 1 + self.kernel
in_w = h - 1 + self.kernel
in_gradient = np.zeros((in_h,in_w,self.c_in))
for i in range(self.c_out):
for j in range(self.c_in):
for m in range(self.kernel):
for n in range(self.kernel):
cur_img = self.img[m:m+h, n:n+w,j]
kernel_grad[i][j][m][n] += np.sum(np.multiply(cur_img, gradient[:,:,i]))
new_grad = np.zeros((h+2*self.kernel-2,w*self.kernel-2,c))
for i in range(self.c_out):
for j in range(self.c_in):
for m in range(in_h):
for n in range(in_w):
cur_img = new_grad[m:m+self.kernel,n:n+self.kernel,i]
in_gradient[m,n,j] += np.sum(np.multiply(cur_img, self.filter[i][j]))
return kernel_grad, in_gradient
优化版本
下面的版本来自《深度学习入门:基于python的理论和实现》
def im2col(input_data, filter_h, filter_w, stride=1,pad=0):
N,C,H,W = input_data.shape
out_h = 1+int((H+2*pad-filter_h)/self.stride)
out_w = 1+int((W+2*pad-filter_w)/self.stride)
img = np.pad(input_data,[(0,0),(0,0),(pad,pad),(pad,pad)],'constant') #四个维度的填充,N和C不填充
col = np.zeros((N,C,filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:,:,y,x,:,:] = img[:,:,y:y_max:stride, x:x_max:stride]
col = col.transpose(0,4,5,1,2,3,).reshape(N*out_h*out_w,-1)
return col
def col2im(col, input_shape,fh, fw, stride=1, pad=0):
# n*out*out, cff)
N,C,H,W = input.shape
out_h = 1+int((H+2*pad-filter_h)/self.stride)
out_w = 1+int((W+2*pad-filter_w)/self.stride)
col = col.reshape(N,out_h,out_w,C,fh, fw)
img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
for y in range(filter_h):
y_max = y+stride*out_h
for x in range(filter_w):
x_max = x+stride*out_w
img[:,:,y:y_max:stride, x:x_max:stride]+=col[:,:,y,x,,:,:]
return img[:,:,pad:H+pad,pad:W+pad]
class Convolution:
def __init__(self,w, b, stride=1, pad=0):
self.w = w
# self.w = np.random.randn((out_c, in_c, fh, fw))
self.b = b
self.stride = stride
self.pad = pad
def forward(self,x):
oc, C, fh,fw = self.w.shape
N, C, H, W = x.shape
out_h = 1+int((H+2*self.pad-fh)/self.stride)
out_w = 1+int((W+2*self.pad-fw)/self.stride)
col = im2col(x,fh,fw,self.stride, self.pad)
self.col = col
# n*out_h*out_w, c*k*k
out = col* self.w.reshape(oc,-1).T + self.b
out = out.reshape(N,out_h,out_w, -1).transpose(0,3,1,2)
return out
def backward(self,dout):
oc,C,fh,fw = self.w.shape
dout = dout.transpose(0,2,3,1).reshape(-1,oc)
self.db = np.sum(dout,axis=0)
self.dw = np.dot(dout,self.col.T)
self.dw = self.dw.transpose(1,0).reshape(oc,C,fh,fw)
self.col_w = self.w.reshape(oc,-1).T
dcol = np.dot(dout,self.col_w.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx