AcWing 4405. 统计子矩阵(每日一题)
如果你觉得这篇题解对你有用,可以点点关注再走呗~
题目描述
给定一个 N×M 的矩阵 A,请你统计有多少个子矩阵 (最小 1×1,最大 N×M) 满足子矩阵中所有数的和不超过给定的整数 K ?
输入格式
第一行包含三个整数 N,M 和 K。
之后 N 行每行包含 M 个整数,代表矩阵 A。
输出格式
一个整数代表答案。
数据范围
对于 30%
的数据,N,M≤20,
对于 70% 的数据,N,M≤100,
对于 100% 的数据,1≤N,M≤500;0≤Aij≤1000;1≤K≤2.5×108。
输入样例:
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
输出样例:
19
样例解释
满足条件的子矩阵一共有 19,包含:大小为 1×1的有 10个。
大小为 1×2的有 3个。
大小为 1×3的有 2个。
大小为 1×4的有 1个。
大小为 2×1的有 3 个。
分析
直接暴力枚举
需要枚举上、下、左、右 四个边界
时间复杂度 O(n^4) = O(10^10)
n=500 500^4=62500000000=6.25x10^10必定TLE
我们看能不能优化成三维去做?
500^3=125000000=1.25*10^8
这样看还是过不了
于是引入双指针算法将枚举次数降为1.25*10^8/2
时间复杂度为**O(6*10^7)**
这样便可以过了
优化
双指针算法+前缀和
题目问满足子矩阵中所有数的和不超过给定的整数 K的子矩阵
所以我们用前缀和去处理矩阵内所有数的和
时间复杂度为**O(1)**
双指针怎么实现?
下面让我带你来分析
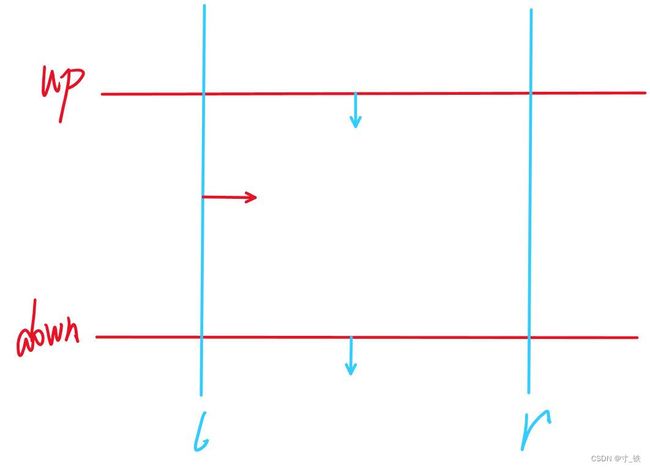
我们需要用到4个变量:
up(矩阵的上界)
down(矩阵的下界)
l(矩阵的左界)
r(矩阵的右界)
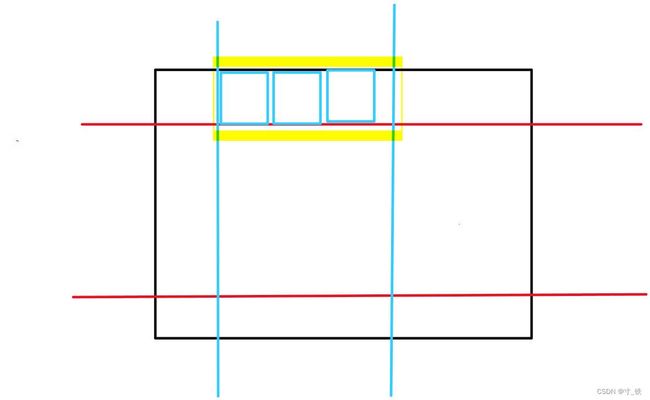
先固定上下界,现在上下界固定下来了。
再依次去枚举上下界,每次枚举上下界时移动左右边界。
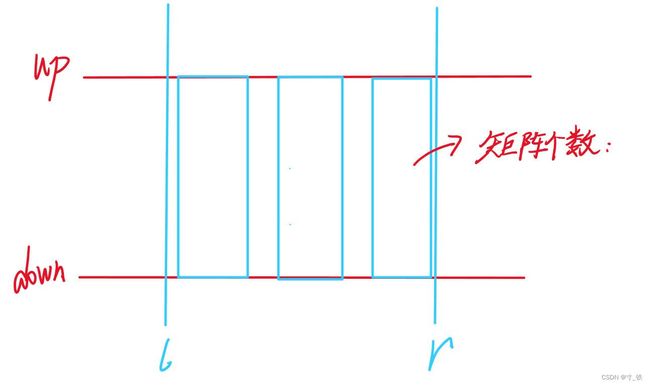
我们需要统计的是左右边界移动的矩阵内有多少列
有多少列就有多少个满足条件的矩阵
矩阵个数:r-l+1
为什么统计的是**矩阵内的列数****见盲点分析
先固定右边界,再去枚举左边界
过程分析
左边界l满足当左边界 l 到右边界 r 这一矩阵内所有数的和> K 时。
说明我们的 l~r 这块矩阵不能包含太多的数,l 需要往右移动。
l 一直移动下去,直至 l 移动到 l~r 这块矩阵的所有数的和值<= k 时,l停止。
在计算完这块矩阵内列的矩阵个数后,再去移动r,依次类推。
确保每次 l~r 这块矩阵内的所有数的和均<=k
这样便可以将矩阵的个数不重不漏的计算出来。
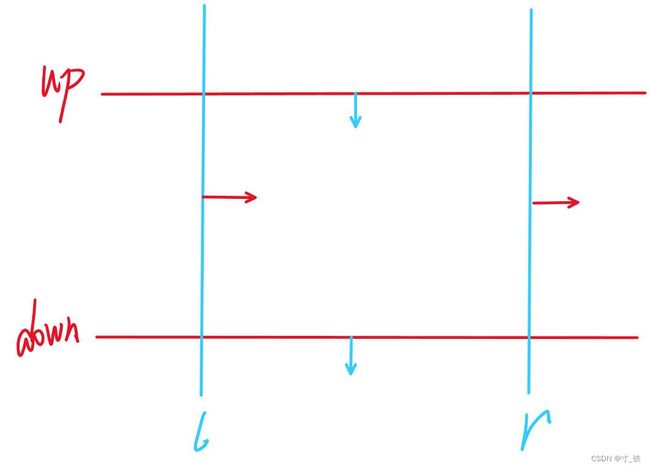
注意
怕很多同学不清楚每一列(个)矩阵代表一列(个)数字
l、r也是一列矩阵,只不过为了便于理解,将l、r抽象成两条线/边界来看
其实l、r本身是一列,是有数字的!!!
下面的分析与此表述同步!
数字图如下:

盲点分析
为什么去枚举l~r的列数?
我们在枚举时枚举的并不全是向前面的图形那样
上面的图形描绘的是整体的矩阵效果,便于理解双指针的移动。
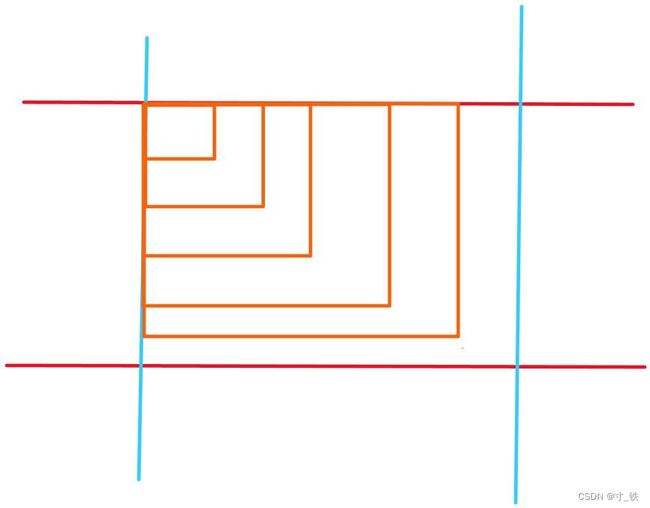
枚举的过程可以抽象看成是在一整个矩阵内拖动橙色长方形,从右上往左下拉。
实际上是由很多的l、r不断分割矩阵的数,见下图:
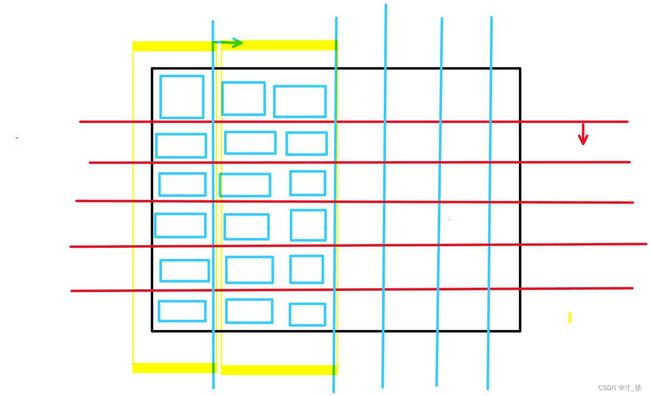
注:图形是便于理解,每一条线不代表一种情况,实际计算时不会重复累加。
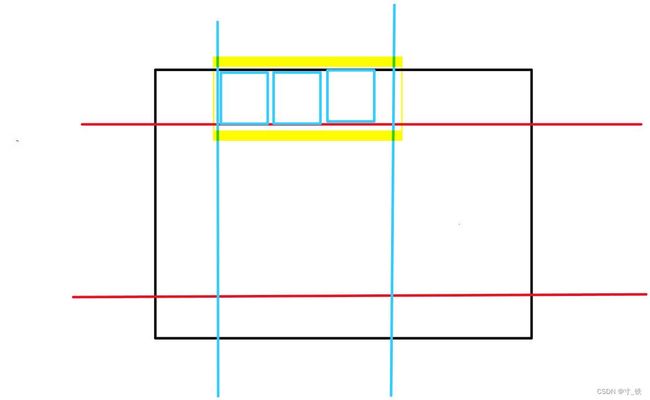
从图中便可以看到,我们将图形理解成动态的过程,从左上到右下不断划分出小矩阵,再去判断是否满足条件,从而将矩阵的总数加起来。
像图中的蓝色小矩阵即是枚举是每一列的矩阵个数,依次移动指针,累加矩阵个数。
注意:l、r也是一列矩阵,是占据了数字的一列。
为什么计算的是列数?
枚举时计算的是每一列的矩阵数,这是因为我们是从右上往左下移动。
如果统计的是每一行的矩阵数则同一行的矩阵数都被并入最终的结果其中,造成结果的错漏,而从每一行去统计矩阵数也与我们枚举时移动的方向不一致,因此不能是统计每一行的矩阵数。同学们仔细想一下对不对?
关于r-l+1的由来:
先看最普遍的情况:
由上图:l在左边,r在右边,中间间隔3列,即3个矩阵,再加上两列其本身所在的那一列矩阵。总共是3+2=5个矩阵,代入公式检验一下,检查一下对不对?
根据图形,假设r=5,l=1,中间的列数分别为2、3、4总共3列
r-l+1=5-1+1=5 结果正确!
再看边界情况:
当r=l时,代入公式r-l+1=0+1=1。
得出1个,而这个便是r、l所在这一列的矩阵,见下图:

注:每一个矩阵代表一个数字
Accode
import java.util.*;
public class Main{
static int N=510;
static int [][]a=new int[N][N];
static int [][]s=new int[N][N];
static int n,m,k;
public static void main(String []args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
k=sc.nextInt();
//预处理前缀和,便于计算矩阵内所有数的和值
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
a[i][j]=sc.nextInt();
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
}
}
long res=0;
//枚举上下边界
for(int up=1;up<=n;up++) {
for(int down=up;down<=n;down++) {
int l=1;//左边界
int r=1;//右边界
while(r<=m) {
//右边界在整个矩阵内
while(l<=r&&!check(up,l,down,r))l++;
//不满足和值小于等于k则移动左边界
res+=(long)r-l+1;
//统计列数
r++;
//左边界固定下来,可以移动右边界
}
}
}
System.out.println(res);
}
static boolean check(int x1,int y1,int x2,int y2) {
//前缀和
long sum=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];
//判断是否满足sum小于等于k这一条件
return sum<=k;
}
}