transformer实现词性标注
1、self-attention
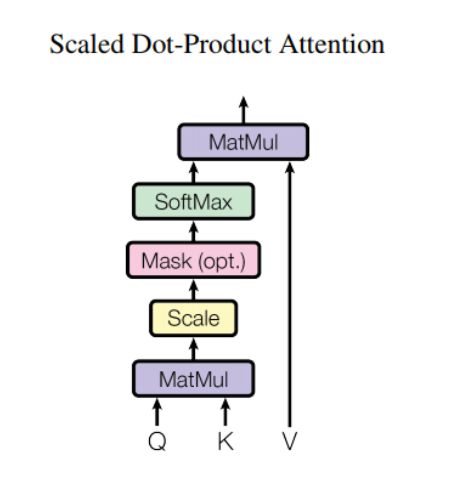
1.1、self-attention结构图
上图是 Self-Attention 的结构，在计算的时候需要用到矩阵 Q(查询), K(键值), V(值)。在实际中，Self-Attention 接收的是输入(单词的表示向量 x组成的矩阵 X) 或者上一个 Encoder block 的输出。而 Q, K, V 正是通过 Self-Attention 的输入进行线性变换得到的。
1.2 Q，K，V的计算
Self-Attention 的输入用矩阵 X进行表示，则可以使用线性变阵矩阵 WQ, WK, WV 计算得到 Q, K, V。计算如下图所示，注意 X, Q, K, V 的每一行都表示一个单词
3.3 Self-Attention 的输出
得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了，计算的公式如下：
公式中计算矩阵 Q和 K 每一行向量的内积，为了防止内积过大，因此除以 dk 的平方根。Q 乘以 K 的转置后，得到的矩阵行列数都为 n，n 为句子单词数，这个矩阵可以表示单词之间的 attention 强度。下图为 Q 乘以 K 的转置，1234 表示的是句子中的单词。
得到 
之后，使用 Softmax 计算每一个单词对于其他单词的 attention 系数，公式中的 Softmax 是对矩阵的每一行进行 Softmax，即每一行的和都变为 1。
对矩阵每一行进行softmax
得到 Softmax 矩阵之后可以和 V相乘，得到最终的输出 Z。
self-attention输出
上图中 Softmax 矩阵的第 1 行表示单词 1 与其他所有单词的 attention 系数，最终单词 1 的输出 Z1 等于所有单词 i 的值 Vi 根据 attention 系数的比例加在一起得到，如下图所示：
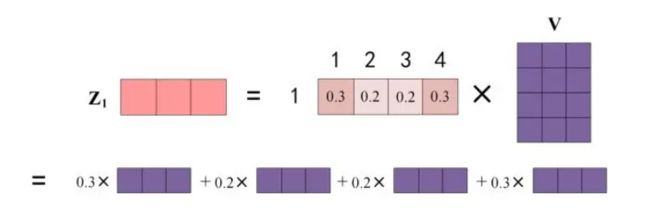Zi的计算方法
class Attention(nn.Module):
def __init__(self, input_n:int,hidden_n:int):
super().__init__()
self.hidden_n = hidden_n
self.input_n=input_n
self.W_q = torch.nn.Linear(input_n, hidden_n)
self.W_k = torch.nn.Linear(input_n, hidden_n)
self.W_v = torch.nn.Linear(input_n, hidden_n)
def forward(self, Q, K, V, mask=None):
Q = self.W_q(Q)
K = self.W_k(K)
V = self.W_v(V)
attention_scores = torch.matmul(Q, K.transpose(-2, -1))
attention_weights = softmax(attention_scores)
output = torch.matmul(attention_weights, V)
return output
2、multi-head attention
从上图可以看到 Multi-Head Attention 包含多个 Self-Attention 层，首先将输入 X分别传递到 h 个不同的 Self-Attention 中，计算得到 h 个输出矩阵 Z。下图是 h=8 时候的情况，此时会得到 8 个输出矩阵 Z。
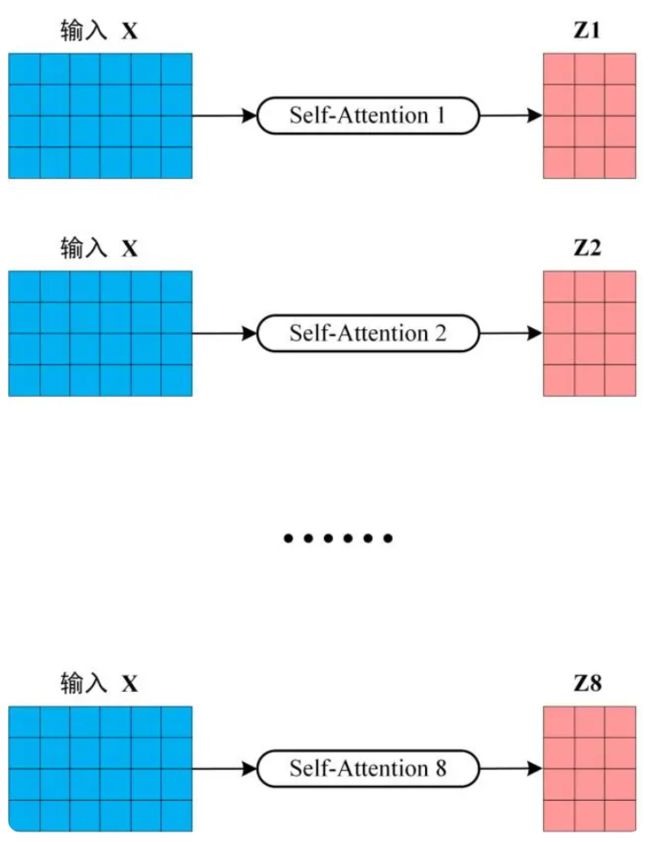多个self-attention
得到 8 个输出矩阵 Z1 到 Z8 之后，Multi-Head Attention 将它们拼接在一起 (Concat)，然后传入一个 Linear层，得到 Multi-Head Attention 最终的输出 Z。
Multi-Head Attention的输出
可以看到 Multi-Head Attention 输出的矩阵 Z与其输入的矩阵 X 的维度是一样的。
class MultiHeadAttention(nn.Module):
def __init__(self,hidden_n:int, h:int = 2):
"""
hidden_n: hidden dimension
h: number of heads
"""
super().__init__()
embed_size=hidden_n
heads=h
self.embed_size = embed_size
self.heads = heads
# 每个head的处理的特征个数
self.head_dim = embed_size // heads
# 如果不能整除就报错
assert (self.head_dim * self.heads == self.embed_size), 'embed_size should be divided by heads'
# 三个全连接分别计算qkv
self.values = nn.Linear(self.head_dim, self.head_dim, bias=False)
self.keys = nn.Linear(self.head_dim, self.head_dim, bias=False)
self.queries = nn.Linear(self.head_dim, self.head_dim, bias=False)
# 输出层
self.fc_out = nn.Linear(self.head_dim * self.heads, embed_size)
def forward(self, Q, K, V, mask=None):
query,values,keys=Q,K,V
N = query.shape[0] # batch
# 获取每个句子有多少个单词
value_len, key_len, query_len = values.shape[1], keys.shape[1], query.shape[1]
# 维度调整 [b,seq_len,embed_size] ==> [b,seq_len,heads,head_dim]
values = values.reshape(N, value_len, self.heads, self.head_dim)
keys = keys.reshape(N, key_len, self.heads, self.head_dim)
queries = query.reshape(N, query_len, self.heads, self.head_dim)
# 对原始输入数据计算q、k、v
values = self.values(values)
keys = self.keys(keys)
queries = self.queries(queries)
# 爱因斯坦简记法，用于张量矩阵运算，q和k的转置矩阵相乘
# queries.shape = [N, query_len, self.heads, self.head_dim]
# keys.shape = [N, keys_len, self.heads, self.head_dim]
# energy.shape = [N, heads, query_len, keys_len]
energy = torch.einsum('nqhd, nkhd -> nhqk', [queries, keys])
# 是否使用mask遮挡t时刻以后的所有q、k
if mask is not None:
# 将mask中所有为0的位置的元素，在energy中对应位置都置为 －1*10^10
energy = energy.masked_fill(mask==0, torch.tensor(-1e10))
# 根据公式计算attention, 在最后一个维度上计算softmax
attention = torch.softmax(energy/(self.embed_size**(1/2)), dim=3)
# 爱因斯坦简记法矩阵元素，其中query_len == keys_len == value_len
# attention.shape = [N, heads, query_len, keys_len]
# values.shape = [N, value_len, heads, head_dim]
# out.shape = [N, query_len, heads, head_dim]
out = torch.einsum('nhql, nlhd -> nqhd', [attention, values])
# 维度调整 [N, query_len, heads, head_dim] ==> [N, query_len, heads*head_dim]
out = out.reshape(N, query_len, self.heads*self.head_dim)
# 全连接，shape不变
output = self.fc_out(out)
return output3、transformer block
3.1 encoder blockg构架图
上图红色部分是 Transformer 的 Encoder block 结构，可以看到是由 Multi-Head Attention, Add & Norm, Feed Forward, Add & Norm 组成的。刚刚已经了解了 Multi-Head Attention 的计算过程，现在了解一下 Add & Norm 和 Feed Forward 部分。
3.2 Add & Norm
Add & Norm 层由 Add 和 Norm 两部分组成，其计算公式如下：
其中 X表示 Multi-Head Attention 或者 Feed Forward 的输入，MultiHeadAttention(X) 和 FeedForward(X) 表示输出 (输出与输入 X 维度是一样的，所以可以相加)。
Add指 X+MultiHeadAttention(X)，是一种残差连接，通常用于解决多层网络训练的问题，可以让网络只关注当前差异的部分，在 ResNet 中经常用到。
残差连接
Norm指 Layer Normalization，通常用于 RNN 结构，Layer Normalization 会将每一层神经元的输入都转成均值方差都一样的，这样可以加快收敛。
3.3 Feed Forward
Feed Forward 层比较简单，是一个两层的全连接层，第一层的激活函数为 Relu，第二层不使用激活函数，对应的公式如下。
Feed Forward
X是输入，Feed Forward 最终得到的输出矩阵的维度与 X 一致。
class TransformerBlock(nn.Module):
def __init__(self, hidden_n:int, h:int = 2):
"""
hidden_n: hidden dimension
h: number of heads
"""
super().__init__()
embed_size=hidden_n
heads=h
# 实例化自注意力模块
self.attention =MultiHeadAttention (embed_size, heads)
# muti_head之后的layernorm
self.norm1 = nn.LayerNorm(embed_size)
# FFN之后的layernorm
self.norm2 = nn.LayerNorm(embed_size)
forward_expansion=1
dropout=0.2
# 构建FFN前馈型神经网络
self.feed_forward = nn.Sequential(
# 第一个全连接层上升特征个数
nn.Linear(embed_size, embed_size * forward_expansion),
# relu激活
nn.ReLU(),
# 第二个全连接下降特征个数
nn.Linear(embed_size * forward_expansion, embed_size)
)
# dropout层随机杀死神经元
self.dropout = nn.Dropout(dropout)
def forward(self, value, key, query, mask=None):
attention = self.attention(value, key, query, mask)
# 输入和输出做残差连接
x = query + attention
# layernorm标准化
x = self.norm1(x)
# dropout
x = self.dropout(x)
# FFN
ffn = self.feed_forward(x)
# 残差连接输入和输出
forward = ffn + x
# layernorm + dropout
out = self.dropout(self.norm2(forward))
return out
transformer
import torch.nn as nn
class Transformer(nn.Module):
def __init__(self,vocab_size, emb_n: int, hidden_n: int, n:int =3, h:int =2):
"""
emb_n: number of token embeddings
hidden_n: hidden dimension
n: number of layers
h: number of heads per layer
"""
embedding_dim=emb_n
super().__init__()
self.embedding_dim = embedding_dim
self.embeddings = nn.Embedding(vocab_size,embedding_dim)
self.layers=nn.ModuleList(
[TransformerBlock(hidden_n,h) for _ in range(n)
]
)
def forward(self,x):
N,seq_len=x.shape
out=self.embeddings(x)
for layer in self.layers:
out=layer(out,out,out)
return out