股票因子--IC分析

导入相关的库

import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings("ignore")

获取基础数据，使用流通市值因子

factor_name = 'mv'  #流通市值

factor = pd.read_csv('mv_zz500.csv', index_col=0)
factor.index = [pd.to_datetime(str(dt)) for dt in factor.index]

if factor_name == 'mv':
    factor = np.log(factor.replace(0., np.nan))  #把0替换成NaN，因为0无法取log
    
stocks = factor.columns.tolist()  #获取股票代码列表

factor.head(3)

# 查看是否有缺失值
factor.isna().any().any()

# 获取中信一级行业分类信息
industry_info = pd.read_csv('info_zz500.csv', index_col=0)
industry_info.head(3)

进行数据预处理

1）去极值

# 定义函数，for循环也可用pandas的向量化操作

def winsorize(df):
    new_data = []
    for i in range(len(df)):
        df_i = df.iloc[i, :]
        df_i_median = df_i.median()
        mad = (df_i - df_i_median).abs().median()
        
        max_range = df_i_median + 5 * mad
        min_range = df_i_median - 5 * mad
        df_i_new = np.clip(df_i, min_range, max_range)
        
        new_data.append(df_i_new)
        
    new_df = pd.concat(new_data, axis=1).T
    return new_df  

factor1 = winsorize(factor)
factor1.head(3)

factor1.T.describe()

2）标准化

# 定义函数。for循环课用pd向量化操作

def standardize(df):
    new_data = []
    for i in range(len(df)):
        df_i = df.iloc[i, :]
        mu = df_i.mean()
        sigma = df_i.std()
        df_i_new = (df_i - mu)/sigma
        
        new_data.append(df_i_new)
        
    new_df = pd.concat(new_data, axis=1).T
    return new_df

factor2 = standardize(factor1)
factor2.head(3)

factor2.T.describe().iloc[:,0:5]

3）缺失值填充

factor3 = factor2.fillna(0)
factor3.T.describe().iloc[:, 0:5]

4）预处理函数封装

def preprocess(df):
    return standardize(winsorize(df))
#     return standardize(winsorize(df)).fillna(0)  #如果涉及填充NaN的话

factor_processed = preprocess(factor)
factor_processed.T.describe().iloc[:,0:5]

结果如下

因子IC分析（IC=corr(dt,Rt+1)）

1）读取收益率

# 收益率矩阵
ret = pd.read_csv('returns_zz500.csv', index_col=0)
ret.index = [pd.to_datetime(str(dt)) for dt in ret.index]
ret = ret * 0.01

# 下个交易日收益率矩阵
tmr_ret = ret.shift(-1)

print(factor_processed.shape)
print(tmr_ret.shape)

2）IC累计计算及可视化

IC_series = factor_processed.corrwith(tmr_ret, axis=1)
IC_series.cumsum().plot()

 展示如下

 3）Rank IC：对因子值与明天收益率求rank，然后计算相关系数。两个变量求rank后计算的相关系数为Spearman相关系数。累计Rank IC的结果如下。

 4）计算IR和胜率

IR: information ratio, IC的均值与标准差的比值，衡量IC的稳定性
胜率: IC大于0的比率，与0.5相差越大越好

IR = IC_series.mean()/IC_series.std()
print('IR is :', IR)
IR = rank_IC_series.mean()/rank_IC_series.std()
print('Rank IR is:', IR)
win_rate = (rank_IC_series > 0).sum()/rank_IC_series.count()
print('win rate is:', win_rate)

计算结果为：

IR is : -0.23846143211969653
Rank IR is: -0.1587782467617657
win rate is: 0.4444444444444444

5）考虑行业中性

需要把原始因子对行业哑变量和市值变量一起回归，回归残差作为新的因子

# 将行业信息按照stocks名称重新排列（一个是factor表，一个是industry_info表）,stocks里面为从factor表中取出的所有股票的股票代码
industry_info = industry_info.set_index('S_INFO_WINDCODE').reindex(index=stocks)
industry_info.head(5)

# 对每天先按照行业对列分组 -- by=industry_info['INDUSTRIESNAME'], axis=1
# 然后行业内，对每只股票减去行业均值 -- x.sub(x.mean(axis=1), axis=0)
factor_rank_ind = factor_processed.groupby(
    by=industry_info['INDUSTRIESNAME'], 
    axis=1,
    group_keys=False,
    ).apply(lambda x: x.sub(x.mean(axis=1), axis=0))

factor_rank_ind.head(3)

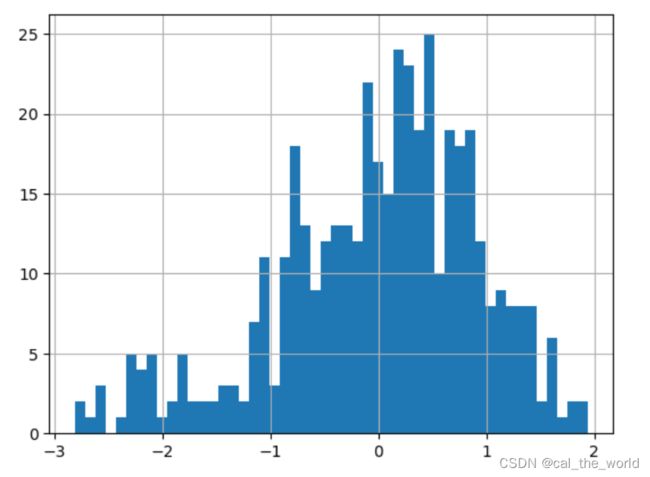
factor_rank_ind.iloc[0].hist(bins=50)

取出行业均值的Rank IC满足如下直方分布

 计算秩的相关性并可视化行业中性后的累积Rank IC

rank_IC_series1 = factor_rank_ind.corrwith(tmr_ret, axis=1, 
                                          method='spearman')
rank_IC_series1.cumsum().plot()

最后计算行业中性后的IR

IR = rank_IC_series1.mean()/rank_IC_series1.std()
print('Rank_ind IR is:', IR)

结果为：

Rank_ind IR is: -0.15211939082931858