C++--动态规划背包问题(1)

1. 【模板】01背包_牛客题霸_牛客网

你有一个背包，最多能容纳的体积是V。

现在有n个物品，第i个物品的体积为vivi​ ,价值为wiwi​。

（1）求这个背包至多能装多大价值的物品？

（2）若背包恰好装满，求至多能装多大价值的物品？

输入描述：

第一行两个整数n和V，表示物品个数和背包体积。

接下来n行，每行两个数vivi​和wiwi​，表示第i个物品的体积和价值。

1≤n,V,vi,wi≤10001≤n,V,vi​,wi​≤1000

输出描述：

输出有两行，第一行输出第一问的答案，第二行输出第二问的答案，如果无解请输出0。

示例1

输入：

3 5
2 10
4 5
1 4

输出：

14
9

说明：

装第一个和第三个物品时总价值最大，但是装第二个和第三个物品可以使得背包恰好装满且总价值最大。 

示例2

输入：

3 8
12 6
11 8
6 8

输出：

8
0

说明：

装第三个物品时总价值最大但是不满，装满背包无解。 

分析：对于背包问题，这道题十分重要，分析过程看下图：

#include 
#include 
#include 
#include 
using namespace std;
const int V=1010;//体积
int n=0;
int v=0;
int num[V];//体积
int val[V];//价值
int main()
{
    cin>>n;
    cin>>v;
    for(int i=0;i>num[i]>>val[i];
    }   
    int dp[V];
    //第一题
    memset(dp,0,sizeof dp);//初始化
    for(int i=1;i<=n;i++)
    {
        for(int j=v;j>=num[i-1];j--)
        {
            dp[j] = max(dp[j],dp[j - num[i-1]] + val[i-1]);
        }
    }
    cout<=num[i-1];j--)
        {
            
            if(dp[j - num[i-1]] != -1)
                dp[j] = max(dp[j],dp[j - num[i-1]] + val[i-1]);
        }
    }
    cout << (dp[v] == -1 ? 0 : dp[v]) << endl;
    return 0;
}

2.分割等和子集  力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

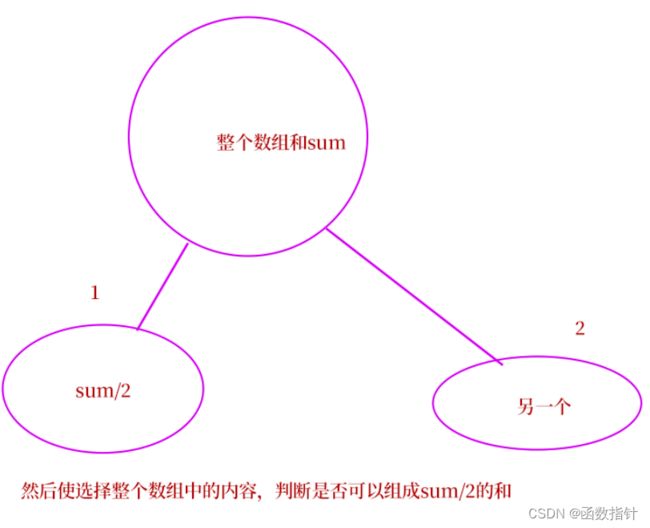
分析：对于这道题而言，需要解决的问题是如何转化为背包问题，这道题要求分割数组，使两个子数组的大小相等，所以我们可以求出数组元素和，然后除以2，判断是否可以整除，如果不可以，则返回false;可以整除2则适用背包问题：

class Solution {
public:
    bool canPartition(vector& nums) 
    {
        int n=nums.size();
        int sum=0;
        for(const auto& s:nums) sum+=s;
        
        if(sum%2==1)
            return false;
        sum=sum/2;
        //初始化
        vector dp(sum+1);

        dp[0]=true;

        for(int i=1;i<=n;i++)
        {
            for(int j=sum;j>=nums[i-1];j--)
            {
                    dp[j]=dp[j]||dp[j-nums[i-1]];              
            }
        }
        return dp[sum];
    }
};

3.目标和  力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

• 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入：nums = [1], target = 1
输出：1

分析：

class Solution {
public:
    int findTargetSumWays(vector& nums, int target) 
    {
        int sum=0;
        int n=nums.size();
        //转化为背包问题
        for(int i=0;i dp(sum+1);
        dp[0]=1;
        for(int i=1;i<=n;i++)
        {
            for(int j=sum;j>=nums[i-1];j--)
            {
                 dp[j]+=dp[j-nums[i-1]];
            }
        }
        return dp[sum];
        
    }
};

4.最后一款石头的重量(2)  力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

示例 1：

输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2：

输入：stones = [31,26,33,21,40]
输出：5

分析：

class Solution {
public:
    int lastStoneWeightII(vector& stones) 
    {
        int sum=0;
        int n=stones.size();
        for(int i=0;i dp(sum+1);
        for(int i=1;i<=n;i++)
        {
            for(int j=sum;j>=stones[i-1];j--)
            {
                dp[j]=max(dp[j],dp[j-stones[i-1]]+stones[i-1]);
            }
        }
        return enquesum-2*dp[sum];
    }
};