C语言之练习题

欢迎来到我的：世界

希望作者的文章对你有所帮助，有不足的地方还请指正，大家一起学习交流 !

---

前言

这期文章由：两题问答题+四道编程题；小孩在文章中写有详细解题思路，感谢大家支持支持。

---

简答题

第一题

思路：

首先我们要知道x=x&(x-1)的含义；
假设x=3；也就是 011；
而x-1=2；是010；
而x&(x-1)，按照&的运算原则；有0则为0，两者都为1，则为1;那么运算结果为010；

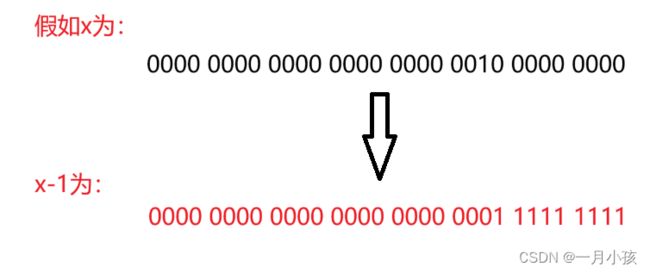
• 这时在来看看x-1，如果原x的最后一位为1，那么就是将最后一位改为0；
• 那如果x不是最后一位为0，那么其减1取决于其上一位，如果其上一位还是为0，就再往前找，直到找到1，然后将这位改为0，然后将其后都改为1；
  总结:这个二进制的最后一个1变成了0，之后的数都变成了1;
  
• 综上所述x=x&(x-1)就是：将 xx 的二进制表示的最后一个 1 变成 0 。

---

现在我们看看该函数：先x=-1,补码：0xFFFFFFFF;
x-1=-2，补码：0xFFFFFFFD；
新的x=x&(x-1); 0xFFFFFFFF & 0xFFFFFFFD=0xFFFFFFFD;
这时也就是将1111 1111 1111 1111 1111 1111 1111 1110，就将最后一位1改为0；
这个循环里，直到最后将-1的补码全部转为0，就会跳出循环了；
这里应该有32次循环；

---

第二题

下列函数输出的结果是（ ）？

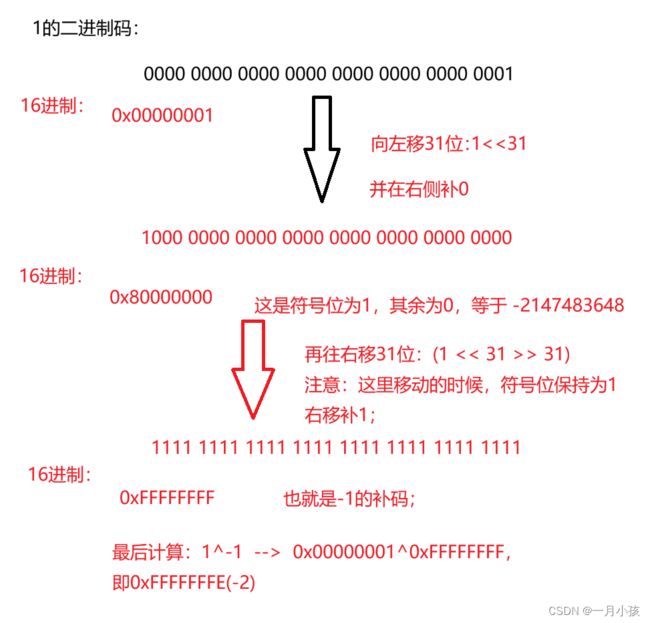
思路：

这道题考察的是我们对二进制移位的了解程度；

编程题

第一题

---

地址：oj地址

---

解题思路：排序
因为我们需要返回下标，所以我们不能再原数组进行排序，重新开辟一个新数组num；
将原数组nums所有拷贝到num里，在对num进行排序；设置最后一位下标为end，再比较end和(end-1)上的值；如果满足num[end-1]*2 <= num[end] ，就只需要在原数组中找到这个值的下标并返回；如果不满足就返回-1；
注意：如果数组元素<=1；就返回0；

代码实现：

int imp(const void* e1, const void* e2)
{
    return *(int*)e1 - *(int*)e2;
}

int dominantIndex(int* nums, int numsSize) {
    if (numsSize <= 1)//如果数组中元素只有一位就返回0；
    	return 0;
    int num[100];//创造一个新数组进行排序；
    int i = 0;
    for (i = 0; i < numsSize; i++)//拷贝进新数组
    {
        num[i] = nums[i];
    }

    qsort(num, numsSize, sizeof(int), imp);//进行排序
    int end = numsSize - 1;//设置end为最后一个下标；
    float sum=num[end-1]*2;//
    if (sum <= num[end])
    {
        for (i = 0; i < numsSize; i++)//在原来数组中找到相同的值
        {
            if (num[end] == nums[i])
            {
                return i;//找到原下标并返回；
            }
        }
    }
    return -1;//否则返回-1；
}

第二题

---

地址：oj地址

---

解题思路：

注意：自除数里不包含0。
根据自除数的定义，如果一个整数不包含 0 且能被它包含的每一位数整除，则该整数是自除数。 判断一个整数是否为自除数的方法是遍历整数的每一位，判断每一位数是否为 0 以及是否可以整除该整数。
遍历每一位整数的方法是：每次将当前整数对 10 取模即可得到当前整数的最后一位，然后将该整数除10，重复该操作，直到当前整数变成 0时，就代表了遍历完了整数的每一位，遍历完后就将该整数存入要返回的数组；

代码实现：

int* selfDividingNumbers(int left, int right, int* returnSize){
    int *arr=(int*)malloc(sizeof(int)*(left+right));//开辟一块足够大小的空间
    int i=0;
    int j=0;
    for(i=left;i<=right;i++)//进行遍历
    {
        int n=i;//保存一下该值
        while(n%10!=0 && i%(n%10)==0)//判断该整数不包含0，并且保证整数的每一位都能整除该整数
        {
            if(n/10)
            {
                n/=10;
                continue;
            }
            else
            {
                arr[j]=i;//遍历完该整数，就存入返回数组
                j++;
                break;
            }
        }

    }
    *returnSize=j;
    return arr;
}

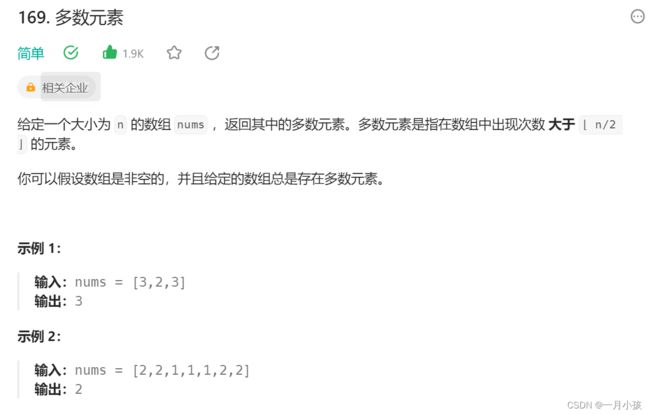
第三题

---

地址：oj地址

---

解题思路：Boyer-Moore 投票算法
把众数记为+1，其他的数记为-1；将它们全部加起来，显然和大于0，从结果本身我们可以看出众数比其他数多。
具体过程：
首先设置一个变量edg为记录众数值；在创造一个count来记录众数的个数，假如数组首元素就是众数，一开始就将count =1;遍历数组时，将edg与nums[i]进行比较，如果相等就+1，如果不同就-1，如果count==0时，需要改众数值，将edg改为nums[i+1]；

代码实现：

int majorityElement(int* nums, int numsSize){

  int edg=nums[0];//假如数组首元素就是众数
  int i=0;
  int count=1;//因为首元素就是众数，已经+1了
  for(i=1;i<numsSize;i++)//进行遍历
  {
    if(edg==nums[i])//相等就+1
    {
      count++;
    }
    else//不等就-1
    {
      count--;
      if(count==0)
      {
        edg=nums[i+1];//修改众数的值
      }
    }
  }

return edg;

}

第四题

---

地址：oj地址

---

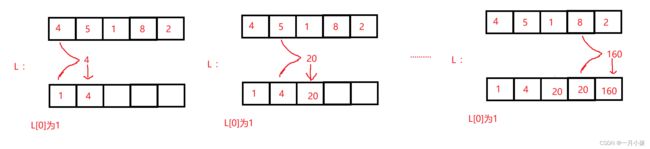
解题思路：左右乘积列表

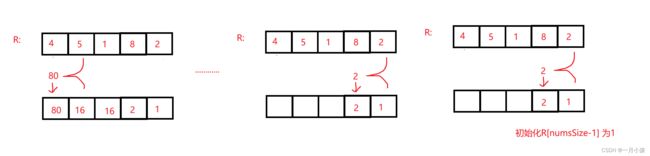
• 初始化两个空数组：L和R。对于定索引 i，L[i]代表的是i左侧所有数字的的乘积；R[i]代表的是i右侧所有数字的乘积；
• 然后两个循环来补充L和R数组，对于L数组L[0]为1，因为第一个元素左边是没有元素的，对于其他的是：L[i]=L[i-1]*nums[i-1];
  

同理R数组R[numsSize-1]为1，因为最后一个元素的右边没有元素，对于其他的是：R[i]=R[i+1]*nums[i+1];

• 补充完L和R后,我们只需要在返回数组上迭代，定索引i处的值：L[i]*R[i];

代码实现：

static int answer[1000000];
int* productExceptSelf(int* nums, int numsSize, int* returnSize){
    
    int L[numsSize];
    int R[numsSize];
    int i=0;
    //左边元素所有乘积
    L[0]=1;
    for(i=1;i<numsSize;i++)
    {
        L[i]=L[i-1]*nums[i-1];
    }

    //右边元素所有乘积
    R[numsSize-1]=1;
    for(i=numsSize-1-1;i>=0;i--)
    {
        R[i]=R[i+1]*nums[i+1];
    }

    for(i=0;i<numsSize;i++)//迭代返回数组
    {
        answer[i]=R[i]*L[i];
    }

    *returnSize=numsSize;
    return answer;
}

总结

在这期文章中写了几道编程题，如果还有更好的方法的老铁，可以在评论区里面一起进行讨论哦，在后面随着小孩的知识储备越多，小孩肯定还会加以优化优化！！

---

到了最后：感谢支持

我还想告诉你的是：
------------对过程全力以赴，对结果淡然处之
也是对我自己讲的