每日刷题：第二十三、二十四天 详解KMP算法中next数组

今日不刷题了，对前两天的KMP算法进行详解，我搜遍了全网，对于next数组的建立只有说明如何建立的，却没有说明为什么这样建的，今天我们将会从

1. 暴力枚举的弊端
2. KMP算法的引入及优势
3. KMP算法的实现
4. nxet数组的创建

几个方面来讲解，本人能力有限，若有错误也麻烦各位大佬及时指出
需要看对应内容的老哥直接移步到对应的地方即可，本文重点在于讲解next数组的建立，所以其他地方也只是大概提一提，不周到之处，麻烦谅解

暴力匹配的弊端

这是一道经典的字符串匹配问题

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

让我们先使用暴力匹配来做一次，两层for循环，若当前第一位相同则比较之后的，若到末尾一直相同则返回true，若中途有不相等的，那么top指针指向下一个字符继续开始遍历，bottom指针回到首字符重新开始匹配（暴力匹配很简单，所以只简单用文字表达了）

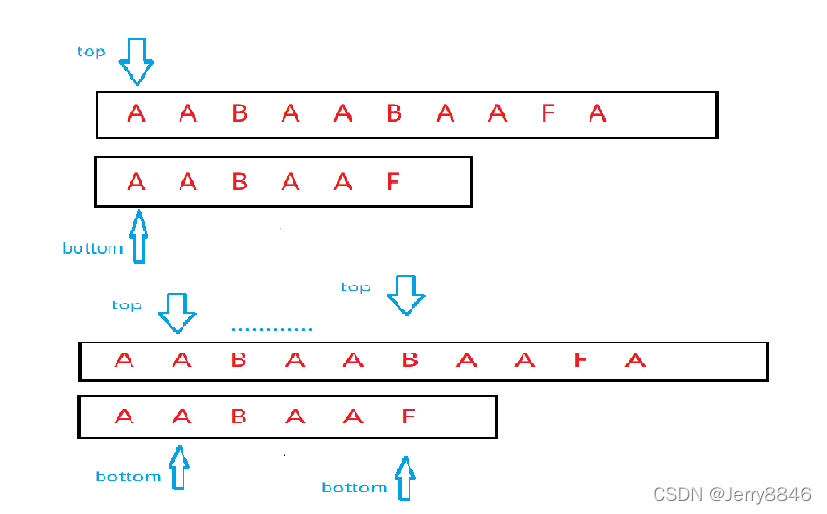
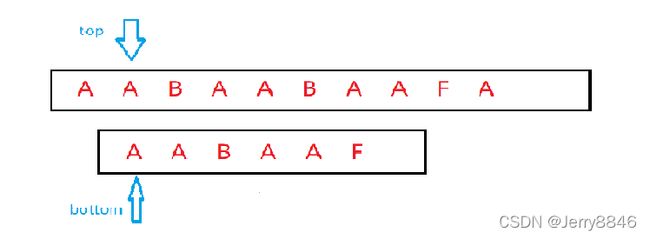
如果出现图中这种情况，我们发现头尾指针会反复回溯，去反复的查看一些已经验过的字符是否相同，这大大的降低了我们的匹配效率，那么有没有一个办法使得我们尽可能的减少回溯呢？

KMP算法的引入及优势

KMP算法就是一种top指针不回溯的算法，首先我们会构造一个模式串的（短的那个）最长公共前后缀表(next[])。
如上面这个例子，他的最长公共前后缀表（之后简称前缀表）如图:

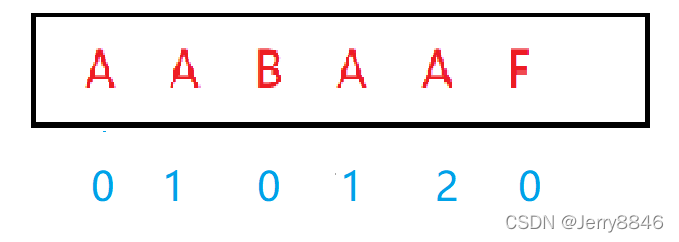
那么它是怎么来的呢？

什么是前缀，除了最后一个字符之外都叫前缀，eg. A、AA、AAB、AABA、AABAA
什么是后缀，除了第一个字符之外都叫后缀， eg.F、AF、AAF、BAAF、ABAAF

所以对于"AABAAF"整个字符串而言，他的最长公共前后缀为0

那其他数字怎么来的？

每个字符下面的数字代表，从第一个字符开始到这个字符的最长前后缀

以上面式子为例：

对于"A" 它的最长前后缀为0（它就一个字符嘛，又没前缀，又没后缀，肯定为0）
对于"AA" 它的最长前后缀为1 （A和A）
对于"AAB" 前缀：A AA 后缀： B AB 所以最长前后缀0
对于"AABA" 前缀：A AA AAB 后缀：A BA ABA 所以最长前后缀为1
对于"AABAA" 前缀 A AA AAB AABA 后缀 A AA BAA ABAA 所以最长前后缀为2
对于整个字符串，上面已经说了为0，那么前缀表就出来了

前缀表的意义及作用

意义：前缀表记录了前面字符串的前后相同情况，以上面为例

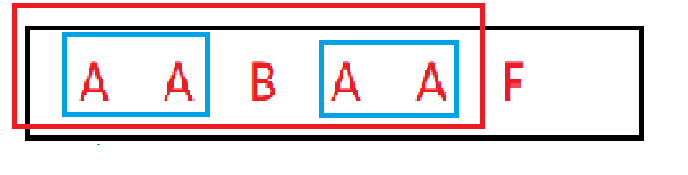
最后一个A下面的2告诉我们前面长度为2的字符子串与后面长度为2的字符子串(图中的两个AA)是相等的

作用：减少回溯

我们跟之前一样匹配，遇到相同的就同时++，遇到不相同的此时要回溯吧，那么回溯到哪里呢？
先说答案：上指针不动，下指针挪到==next[bottom-1] (next数组也就是之前的前缀表)==的位置

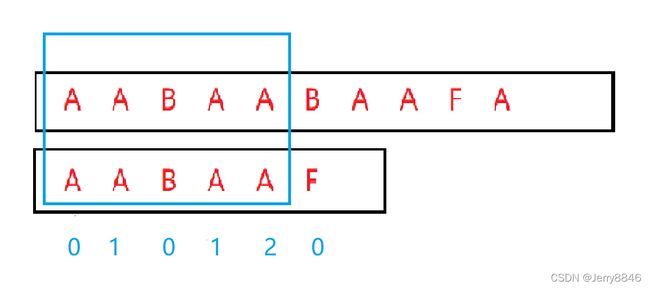
原因：因为前面的部分都相同，而前缀表告诉我们，前后相等的字符子串最长为2，那这相同的部分我们就不用再去匹配了，保持上指针不动，下指针挪到next[2]的位置（2其实是一种“巧合”，得益于数组0开始的设计才能完成的）

KMP算法的实现

其实规则刚刚已经说了：就是上指针永不回溯，遇到不相等时下指针回溯到前一个字符指向的next值的位置（即next[bottom-1]）

对于具体的实现我们会对next数组做一些优化：(第24天续)
第一种方案就是什么都不做，拿前缀表直接作为next数组
第二种方案就是整体右移一位，第一位赋值为-1（就不用再回头取值了）

Next数组的建立

实操过代码的同学，一定知道KMP算法的最难点就是构建next数组，网上有一些已有的方案，却没有讲清楚这些方案的真正思路，所以建立next数组就是本文章的重中之重

首先，我们看一下一种被广泛运用的next数组的建立方案，之后我们再去剖析每一步的其中意味，让我们更深刻的理解前人总结的方案的妙处

通法：

① 初始化（左右指针就位）
② 前后缀不相等情况的处理
③ 前后缀相等时情况的处理

具体代码：

    private List getFrontTable(String needle)
    {
        //构建前缀表数组
        List frontTable = new ArrayList<>(needle.length()+1);
        //初始化
        int left = 0;//左指针：指向前缀的末尾
        int right = 1;//右指针：指向后缀的末尾
        //添加一个0结点
        frontTable.add(0);
        //构建前缀表
        for(;right < needle.length();right++)
        {
            //前后缀不相等的处理
            while(left > 0 && needle.charAt(left) != needle.charAt(right))
            {
                left = frontTable.get(left - 1);//理解难点，大概也是KMP的思路，想不明白想跳过，后面会详解
            }
            //前后缀相等情况的处理
            if(needle.charAt(left) == needle.charAt(right))
            {
                left++;
            }
            //记录下前缀表长度
            frontTable.add(left);
        }
        return frontTable;
    }

剖析

（图中上面数组为所有后缀，下面数组所有前缀，分为两个方便大家看，也方便我讲解）
首先我们定义了两个指针，left指向的是前缀的末尾，right指向的是后缀的末尾（请大家在脑袋里想象出指向各自的情景）
如果大家想象力不错的话，不难想出，当前我们计算的就是0~right指向的字符子串的最长前后缀（eg.当前计算的是"AA"的最长前后缀）

对于left它还有特殊意义，因为在left，right指向的值相同的时候，left会+1，(注：此时right还没有+1)那么对于此时的子串，left的大小就等于最长前后缀
eg. 如上图，此时二者相等，left+1，那么对于AA这个子串，他的最长前后缀就是1
这就是为什么我们可以在二者相等的时候，让left作为最长前后缀了

那不对啊老哥，二者不相等的时候，你怎么也拿left当最长前后缀了？

我们来看看不相等具体是什么情况：
①二者不相等，left一直回溯回溯到二者相等为止
②left回溯到0，不能再回溯了
①不解释，第二种情况那就说明此时最长相等前后缀为0

我们模拟运行一下：

当前left = right，所以left++，记录下left的值，right继续向后遍历一位（查看AAB的最长前后缀），此时left，right不相同 (因为AB != AA) ，那left是不是应该回溯，看看AAB有没有其他的前缀能和后缀相等,所以它往前回溯（这里我们先忽略上面那种妙法，就先抽象的理解它是往前找有无相等前缀的），那么往前回溯了，发现left还是不等于right，此时left不能再回溯了，那就说明当前的最长相等前后缀为0

通过以上例子，我们讲明白了，为什么是left回溯，因为它要去前面寻找有没有其他前缀能和后缀相等的

那为什么不是right回溯呢？

因为right定义的是后缀的末尾，right回溯了，那么当前计算的字符子串就变化了(当前计算的字符子串为0~right的位置)

最后一个问题？left应该怎么回溯？？

几个已知条件
①left回溯的时候，那么left一定大于0，也就是说next[left-1]是有意义的
②next[left-1]的意义就是0~left-1字符子串的最大相等前后缀
③left需要回溯的时候，前面已经有许多相等的字符了

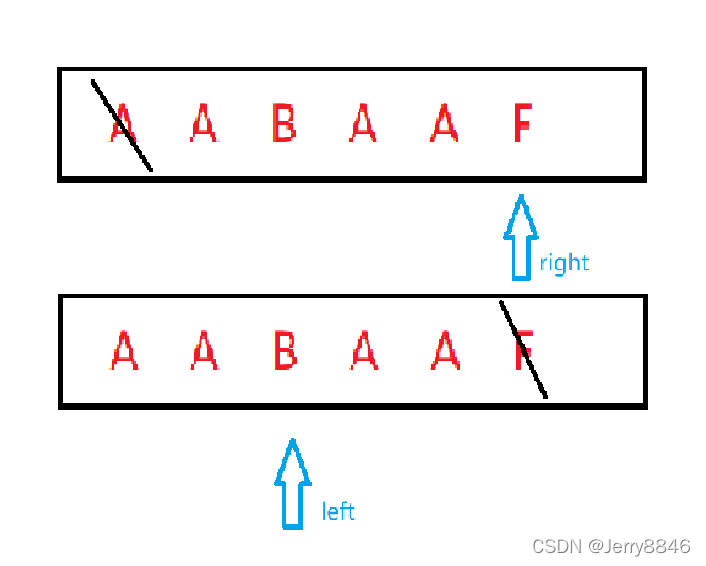
还是用上面例子来讲，走到最后如图：
left和right不相等（AAB和AAF不相等），那么left就需要回溯到上一个A的后面（也就是说AAF和AAB不相等了，那我们现在想去验证前面是否存在"AF"，所以需要走到上一个A的后面去看当前位是否为F），发现上一个A的后面也不是F

此时left和right还是不相等（AA和AF不相等），前面又没有A了
，那left只能回溯到0，看第一位是不是和最后一位相等（A和F相不相等）发现不相等，好，记录为0

到此为止，这个通法的意思我大概就讲明白了，但难免还是会有疏漏，大家也得给自己多提问题。

例如：为什么最后一个我们只比较了AAB和AAF，而没有比较BAAF和AABA呢？
答案其实很简单，那就是我们在比较第一个A和第一个B时，发现二者不相等，然后这个组合就给pass掉了

另外脑袋里多去模拟，多去敲一下代码debug一下，就能吃透了，本文一共写了七个多小时，一直在反复思考如何更加通俗的理解next数组的建立，希望对大家有所帮助

最后附上之前欠的题目KMP解法：
Strstr:

class Solution {
    public int strStr(String haystack, String needle) {
        //构建前缀表数组
        List frontTable = getFrontTable(needle);
        //构建上下双指针
        int top = 0;
        int bottom = 0;
        //遍历上指针
        while(top < haystack.length() || bottom == needle.length())
        {
            //若下指针等于整个字符串长度了，说明找到了
            if(bottom == needle.length())
            {
                return top - needle.length() ;
            }
            //若上下指针的内容相等，则共同++
            if(haystack.charAt(top) == needle.charAt(bottom))
            {
                top++;
                bottom++;
                continue;
            }else
            {
                //若bottom为0，则top++，bottom = top
                if (bottom == 0)
                {
                    top++;
                    bottom = 0;
                    continue;
                }
                //若不相等，上指针不变，下指针回溯到前缀表当前位置的值的位置
                bottom = frontTable.get(bottom-1);
            }

        }
        //上指针遍历结束还未找到相同的，说明不存在
        return -1;

    }
    //返回前缀表
    private List getFrontTable(String needle)
    {
        //构建前缀表数组
        List frontTable = new ArrayList<>(needle.length()+1);
        /*
            初始化
        */
        int left = 0;//左指针：指向前缀的末尾
        int right = 1;//右指针：指向后缀的末尾
        //添加一个0结点
        frontTable.add(0);
        //构建前缀表
        for(;right < needle.length();right++)
        {
            //前后缀不相等的处理
            while(left > 0 && needle.charAt(left) != needle.charAt(right))
            {
                left = frontTable.get(left - 1);//理解难点，大概也是KMP的思路，想不明白想跳过，后面会详解
            }
            //前后缀相等情况的处理
            if(needle.charAt(left) == needle.charAt(right))
            {
                left++;
            }
            //记录下前缀表长度
            frontTable.add(left);
        }
        return frontTable;
    }
}