图神经网络和分子表征：4. PAINN

如果说 SchNet 带来了【3D】的火种，DimeNet 燃起了【几何】的火苗，那么 PAINN 则以星火燎原之势跨入 【等变】时代。

在 上一节 中，我们提到， PAINN 在看到 DimeNet 取得的成就之后，从另一个角度解决了三体几何问题，顺带着建立起了一个真正超越不变网络的等变模型。在本篇博客中，我们将详细解读 PAINN 原文，并简单罗列其核心代码结构。

PAINN 故事背景

虽然 PAINN 作者不会在文章里写，他们的灵感源泉，他们受哪篇论文启发。但 PAINN 字里行间都透露着对 DimeNet 的模仿。

例如，PAINN 的 Table 1, Figure 1 都在讲，我这个模型是如何处理角度信息的，以及这种处理方式的优越性。甚至整个 Figure 4 都在 diss DimeNet。虽然这么说显得笔者非常不专业，但笔者依然认为，PAINN 这篇工作就是受 DimeNet 启发展开的。

那 DimeNet 是怎么引入三体信息的呢？下面请允许我进行简单的 前情回顾 。

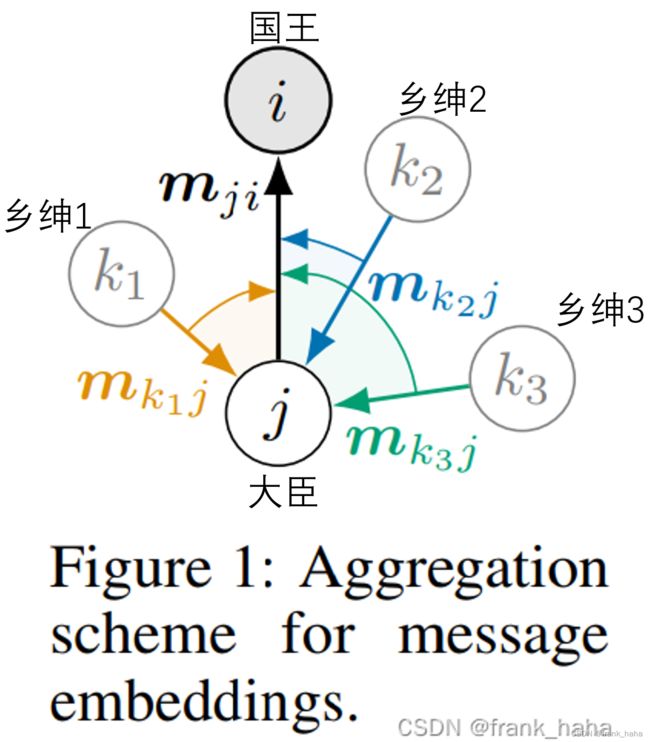
我们套用简单的国王-大臣-乡绅模型。
国王（i）要向下收税，委托大臣（j）办事，大臣收集完各个乡绅的税（$m_{k_{1}j}$, $m_{k_{2}j}$, $m_{k_{3}j}$）以后进行整合（$m_{ji}$），最后传给 国王 （i）。
这其中涉及到了简单的三体信息，即国王、大臣和乡绅构成的夹角。
PAINN 巧妙地利用 2-hop 的消息传递模型将角度信息纳入，在多个数据集上取得了当年的 SOTA.

谁看谁不眼馋啊！

作为 AI for Molecular property 的老祖师爷，schnet 的课题组很快跟进了这项工作，只不过他们看待问题的视角更加物理。

PAINN 的故事

可极化

Schnet 的一作叫 Schutt ，但在很多场合里，Schutt 并不说 Schnet 是 Schutt，而说是 Schrodinger（薛定谔） Net 。借此可见他们讲故事的能力。

那这个 PAINN 是什么的缩写呢？官方给的解释是：Polarizable Atom Interaction Neural Network (PAINN) 可极化原子相互作用神经网络。

在 Schutt 课题组的文章中很少出现 message passing 的字眼。因为他们认为，原子 A 传给原子 B 的信息，事实上是原子 A 与 原子 B 的相互作用（Interaction），所以大家看 SchNet 和 DTNN 这两篇论文经常会云里雾里，啥是相互作用（Interaction）？啥又是连续卷积？不明觉厉！

实际上所谓的相互作用（Interaction）就是原子之间的消息传递，所谓的连续卷积就是构建消息的时候使用 MLP 和一个衰减函数对距离的 embedding 做了一个过滤，连续二字指 MLP 中的激活函数换成了连续可到的 shifted softplus 函数（就是换了一个激活函数）（详情见系列第2篇文章）

那么 PAINN 中的可极化原子又是啥嘞？听起来文邹邹的。

这里要再回顾一下之前的模型，在 PAINN 之前，大家 embedding 原子的时候都会调用 pytorch 里默认的一个 look up table：

from torch.nn import Embedding

点进去这个模块，注释是这样写的：

class Embedding(Module):
    r"""A simple lookup table that stores embeddings of a fixed dictionary and size.

    This module is often used to store word embeddings and retrieve them using indices.
    The input to the module is a list of indices, and the output is the corresponding
    word embeddings.

也就是说，对于同样的输入，这个类会返回同样的一个 embedding 向量。

同样的原子得到的初始的特征向量是一致的，因为原子所处环境不同，多轮消息传递后，各个原子的特征向量往往大相径庭，最后对目标性质的预测也是基于原子所携带的这些特征向量进行的（在 schnetpack 里叫 outputnet ）。不过这些都是后话了。重点是，每个原子最开始取的都是一个一维的特征向量。这些特征向量只能代表标量信息，无法代表原子的任何有方向的信息。

PAINN 正是瞄准这一点展开的，即，每个原子最开始取特征向量时，不仅取标量，还要取一个向量。这些向量可以代表原子有方向的性质，例如偶极矩等，还可以更进一步通过张量积的形式表示高阶特征。

作者举了一个例子，电荷密度在空间某处的多级展开。
零阶 q 对应该点处的 电荷
一阶 u 对应该点处的 偶极
二阶 Q 对应四极

之前的工作如果只对原子进行标量特征嵌入的话，最多只能表达电荷密度。但如果给原子一个向量嵌入，可以下探至 偶极，更进一步通过张量积就可以实现 四极 的拟合。

这就是 PAINN 名字中 可极化 的含义。

角度信息的引入

在拿到向量形式的特征向量后，我们可以通过对向量的简单加和完成角度信息的引入，同时能将计算量从 $o(n{k}^2)$ （DimeNet 2-hop）降至 $o(nk)$（1-hop）。

作者在表 1 中详细对比了 3 种方式。

1. 对于键长的变化，只有距离信息能够捕捉。
2. 对于键角的变化，显式的 angle 和隐式的 direction 都能捕捉，但是 隐式的 direction 是 1-hop 的消息传递，只依赖第一圈的邻居，而 angle 则需要 2-hop，两圈的邻居。（虽然comenet里，这一点已经降到了 1-hop）

此外，作者指出，隐式的 direction 还能鉴别出更多的分子结构：

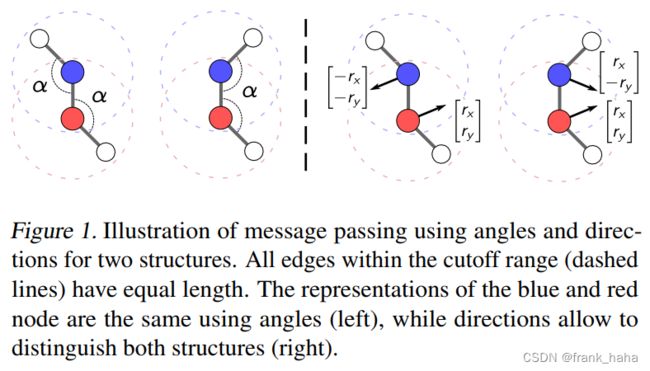
上图中，如果使用显式的 angle，无法鉴别（左）
但如果使用 隐式的 direction （右），则可以很好的鉴别。

这一发现后面衍生出了 Geometric W-L test 的工作：GNN Expressive

等变开山之作？

并不是。在 PAINN 原文中，作者指出，先前已经有很多人尝试了等变表征，但均未取得预期成果：

但 PAINN 的伟大在于，他是第一个将等变模型调参到超越不变模型的。
PAINN 对于等变做了哪些小心翼翼的调整呢？

在消息传递模块，所以对 向量特征 的变换都要遵循线性变化。可以是 scale, 可以是 线性的 MLP，矩阵的线性加和。但不能包含非线性（例如非线性的激活函数）。

另一方面，对于 标量特征 ，可以进行任何的 非线性操作。（上图第一条）

此外，PAINN 在输出时设计了一个巧妙的 模块：

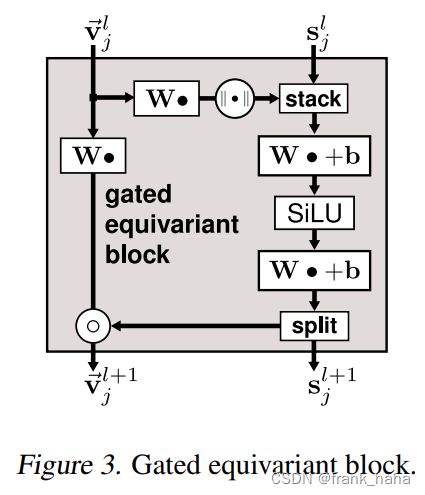
这个模块可以保证等变的向量特征在经过消息传递后，预测向量/张量目标性质时，依然保持等变！这就不得不提到 PAINN 最后一个令人叹服的点了。

不忘初心：解决物理问题

写到这里，我已经吹累了。但还没完。

作为一篇 232 被引的文献，PAINN：

1. 在 1-hop 消息传递成本下，引入了角度信息
2. 首个超越不变模型的等变模型
3. 刷爆了数据集（略夸张）

此外，PAINN 还不忘初心，教大家怎么用“可极化”解决真实的物理问题。

例1：
分子偶极矩的预测。
PAINN 之前：

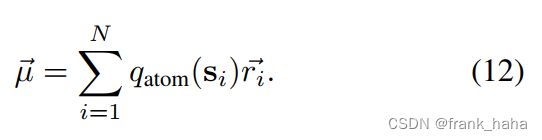
PAINN：

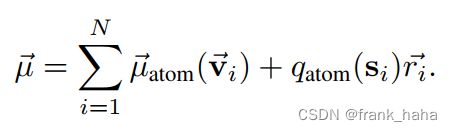
相当于零阶展开进化到1阶展开！

例2：
极化张量：

（翻译累了，自己看吧（其实我也没看懂（捂脸）））
总之就是用张量积将一阶向量升维到了二阶张量。
例3：
拉曼红外也能预测了！！

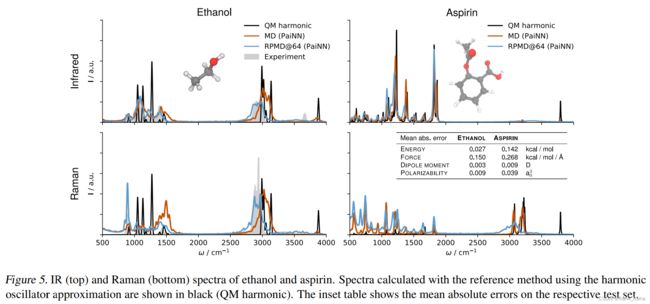
一个字，绝！

好，收，下篇见！