代码随想录day17-二叉树(5)

代码随想录day17-二叉树(5)

今天主要将之前的递归的方法稍微沉淀了一下，以及好好理解了一下回溯的思路。

1、LeetCode 257 二叉树的所有路径

题目分析：

本题就是一个典型的递归加回溯的题目。下面我们来分析一下本题为什么会有回溯呢？
首先我们遍历的是所有路径，比如我们使用前序遍历，先遍历左子树，遍历到了根节点，得到了一条路径，此时的node指向的就是叶子结点，那么我们怎么能进行到下一条路线呢？ 这里就是我们需要考虑的问题。
所以本题需要将路径记录下来，将这条路径走完过后在退回去，这就是回溯的基本思想。
对于本题而言，回溯的思路如下图所示：

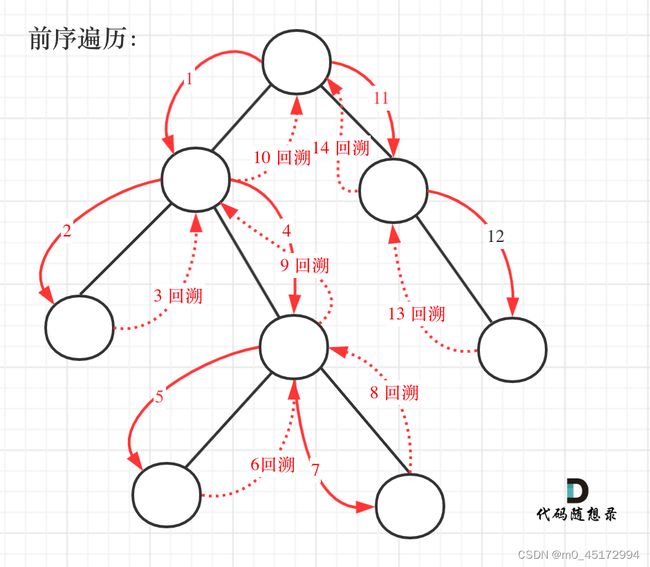
图片来源：代码随想录
下面我们将使用一个代码完整的展示整个回溯的过程，本题可以使用前序遍历。

题目解答：

class Solution {
public:
    void traversal(TreeNode* node, vector<int>& path, vector<string>& ans) {
        path.emplace_back(node->val);  // 中，注意这里要在判断叶子结点之前，否则会漏掉叶子结点
        // 注意这里涉及到一个原则，肯定要保证node不为空，所以在递归的时候，我们就要做限制
        if (node->left == nullptr && node->right == nullptr) {  // 此时是叶子结点
            // 此时的path包含了这一条路径上的点
            string singlePath = "";
            for (int i = 0; i < path.size() - 1; i++) {  // 将前len-1个元素拼凑
                singlePath += to_string(path[i]);
                singlePath += "->"; 
            }
            // 拼凑最后一个
            singlePath += to_string(path[path.size() - 1]);
            ans.emplace_back(singlePath);
            return;
        }

        if (node->left) {  // 左
            traversal(node->left, path, ans);
            path.pop_back();  // 这里为什么要pop呢，体现的就是回溯的过程，因为左孩子走完了之后，还需要看看右边，此时的路径不能走到这下面，需要定位到根结点
        }
        
        if (node->right) {  // 右
            traversal(node->right, path, ans);
            path.pop_back();  // 同样是回溯的体现
        }

    }

    vector<string> binaryTreePaths(TreeNode* root) {
        // 本题就是典型的递归加回溯的题目
        // 使用前序遍历
        vector<int> path;
        vector<string> ans;
        traversal(root, path, ans);
        return ans;
    }
};

其中几个需要注意的点：

1. 中间结点的遍历要放在叶子结点的遍历之前，否则路径会漏掉叶子结点；
2. 我们判断叶子结点使用了left和right，那么我们就必须保证其不为空，所以我们在后面递归的时候，加了条件；
3. 对于某个结点而言，完成了一条路径的遍历，我们就需要回溯，在代码中的具体展示就是将路径的最后一个元素弹出来。

可能i第三个不太好理解，其实我们只要记住，对于递归的单层逻辑，我们不要想那么多。
这里完全就是可以简单理解为，此时node = root，然后我们执行完traversal(node->left, path, ans);之后，就代表我们已经完成了根节点的左结点的遍历，现在path加的是路径，那我们现在要去右边的结点了，那很理所当然即需要将目前的path的最后一个元素弹出，此时最后一个元素就理解成node->left就行了。这就是本题回溯的理解。

下面给出简化的代码（隐藏了回溯的过程）

class Solution {
public:
    void traversal(TreeNode* node, string path, vector<string>& ans) {
        path += to_string(node->val); // 中，注意这里要在判断叶子结点之前，否则会漏掉叶子结点
        // 注意这里涉及到一个原则，肯定要保证node不为空，所以在递归的时候，我们就要做限制
        if (node->left == nullptr && node->right == nullptr) {  // 此时是叶子结点
            // 此时的path包含了这一条路径上的点
            ans.emplace_back(path);
            return;
        }

        if (node->left) traversal(node->left, path + "->", ans);  // 左，回溯的隐藏过程
        if (node->right) traversal(node->right, path + "->", ans);  // 右
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        // 本题就是典型的递归加回溯的题目
        // 使用前序遍历
        string path = "";
        vector<string> ans;
        traversal(root, path, ans);
        return ans;
    }
};

上面的代码看着非常简介，但是却暗藏玄机，完全隐藏了回溯的过程。
首先path没有使用引用的形式，这说明在if (node->left) traversal(node->left, path + "->", ans);进行之后，此时的path还是以前的值，并没有改变，就是这一点点小小的变动，就巧妙的隐藏了回溯的过程。
如果将代码改成：

if (node->left) {
	path += "->";
	traversal(node->left, path, ans); 
}

此时就会出错，因为递归函数执行后，path也就变化了，此时最终的答案就会多一个”->"。
如果非要这么做的话，还需要回溯一下：

if (node->left) {
	path += "->";
	traversal(node->left, path, ans); 
	path.pop_back();  // 回溯">"
	path.pop_back();  // 回溯"-"
}

以上就是本题所有的内容，值得反复去体会其中的含义，以及回溯的过程。

补充一下：我们这里为了保证node->left以及node->right是有意义的，并没有说处理if(node == nullptr)的情况，而是在调用递归函数的时候，就进行了判断，也就是说空的根本不可能会进行调用。那么在之前的前序遍历的时候：

    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }

我们能不能也用这种判断的写法试试呢？

class Solution {
public:
    void traversal(TreeNode* node, vector<int>& vec) {
        vec.push_back(node->val);    // 中
        if (node->left) traversal(node->left, vec);  // 左
        if (node->right) traversal(node->right, vec); // 右
    }
    vector<int> preorderTraversal(TreeNode* root) {
        if (root == nullptr) return {};

        vector<int> result;
        traversal(root, result);
        return result;
    }
};

这样写也是可以的。

2、LeetCode 100 相同的树

题目分析：

本题和101 对称二叉树非常类似，不同的是对称二叉树比较的是外侧和内侧，而本题比较的是同一侧。

题目解答：

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        // 本题和对称二叉树非常类似，不同的是对称二叉树比较的是外侧和内侧，而本题比较的是同一侧
        // 递归的终止条件还是那几个
        if (!p && !q) return true;
        else if (!p && q) return false;
        else if (p && !q) return false;
        else if (p->val != q->val) return false;

        bool leftSide = isSameTree(p->left, q->left);
        bool rightSide = isSameTree(p->right, q->right);
        return leftSide && rightSide;
    }
};

3、LeetCode 572 另一棵树的子树

题目分析：

本题和之前的两个题目非常类似，就是判断子树和已知的树是不是相等。使用深度或者广度搜索遍历每一个结点，然后比较和当前的树是否相等就即可。

题目解答：

广度优先搜索加暴力匹配

class Solution {
public:
    bool isSame(TreeNode* node, TreeNode* target) {
        // 递归的终止条件：一、有一个结点为空
        if (node == nullptr && target != nullptr) return false;
        else if (node != nullptr && target == nullptr) return false;
        // 两个结点都为空，说明是相同的
        else if (node == nullptr && target == nullptr) return true;
        else if (node->val != target->val) return false;  // 两个结点都不是空，但是值不相等

        // 以下就是相等的情况了，进入递归,
        bool leftSide = isSame(node->left, target->left);  // 同时比较同一侧，而不是内外侧
        bool rightSide = isSame(node->right, target->right);
        return leftSide && rightSide;
    }

    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if (subRoot == nullptr) return true;
        // 广度优先搜索加暴力匹配
        queue<TreeNode*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (isSame(node, subRoot)) return true;
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return false;
    }
};

深度优先搜索加暴力匹配

class Solution {
public:
    bool isSame(TreeNode* node, TreeNode* target) {
        // 递归的终止条件：一、有一个结点为空
        if (node == nullptr && target != nullptr) return false;
        else if (node != nullptr && target == nullptr) return false;
        // 两个结点都为空，说明是相同的
        else if (node == nullptr && target == nullptr) return true;
        else if (node->val != target->val) return false;  // 两个结点都不是空，但是值不相等

        // 以下就是相等的情况了，进入递归,
        bool leftSide = isSame(node->left, target->left);  // 同时比较同一侧，而不是内外侧
        bool rightSide = isSame(node->right, target->right);
        return leftSide && rightSide;
    }

    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if (subRoot == nullptr) return true;
        // 使用前序遍历暴力匹配就行
        stack<TreeNode*> stk;
        stk.push(root);
        while (!stk.empty()) {
            TreeNode* node = stk.top();
            stk.pop();
            if (isSame(node, subRoot)) return true;  // 如果当前的是与子树相等，直接返回即可
            if (node->right) stk.push(node->right);  // 前序遍历先存右结点，再存左结点
            if (node->left) stk.push(node->left);
        }
        return false;
    }
};

以上就是这几个类似的题目的解答。题干涉及对称的树，相等的树，都可以使用一样的方法。

以上几天的题目我们做了很多关于二叉树的深度，高度的题目。深度一般使用前序遍历，主要体现一个回溯的过程，而高度一般就使用后序遍历。当然求二叉树的最大深度也是可以用后序遍历来做的，因为二叉树的高度就是根节点的深度。

此外我们还做了一个关于回溯的题目，在这之前，我们也接触过二叉树的层序遍历，使用递归的方法实现的时候，就体现了回溯的思想；此外在使用前序遍历求深度的时候，也体现了回溯的思想；二叉树的所有路径也是回溯的典型代表，需要反复理解。
但是简短的代码看不出遍历的顺序，也看不出分析的逻辑，还会把必要的回溯的逻辑隐藏了，所以尽量按照原理分析一步一步来，写出来之后，再去优化代码。