卷积神经网络初识

目录导读

【1】导论

【2】卷积运算

【3】非线性激活

【4】池化层

【5】全连接层

【6】神经网络的训练与优化

 

【1】导论

卷积神经网络，也就是convolutional neural networks （简称CNN），现在已经被用来应用于各个领域，物体分割啦，风格转换啦，自动上色等，但是CNN真正能做的，只是起到一个特征提取器的作用！所以这些应用，都是建立在CNN对图像进行特征提取的基础上进行的。

拿到一张图片，要对它进行识别，最简单的栗子是，这张图是什么？

比如，我现在要训练一个最简单的CNN，用来识别一张图片里的字母是X还是O。

我们人眼一看，很简单嘛，明显就是X啊，但是计算机不知道，它不明白什么是X。所以我们给这张图片加一个标签，也就是俗称的Label，Label=X，就告诉了计算机这张图代表的是X。它就记住了X的长相。

但是并不是所有的X都长这样呀。比如说...

 

这四个都是X，但它们和之前那张X明显不一样，计算机没见过它们，又都不认识了。

（这里可以扯出机器学习中听起来很高冷的名词 “ 欠拟合 ”）

 

不认识了怎么办，当然是回忆看看是不是见过差不多的呀。这时候CNN要做的，就是如何提取内容为X的图片的特征。

我们都知道，图片在计算机内部以像素值的方式被存储，也就是说两张X在计算机看来，其实是这样子的。

 

 

其中1代表白色，-1代表黑色。

如果按照每像素逐个比较肯定是不科学的，结果不对而且效率低下，因此提出其他匹配方法。

我们称之为patch匹配。

观察这两张X图，可以发现尽管像素值无法一一对应，但也存在着某些共同点。

 

如上图所示，两张图中三个同色区域的结构完全一致！

因此，我们就考虑，要将这两张图联系起来，无法进行全体像素对应，但是否能进行局部地匹配？

答案当然是肯定的。

相当于如果我要在一张照片中进行人脸定位，但是CNN不知道什么是人脸，我就告诉它：人脸上有三个特征，眼睛鼻子嘴巴是什么样，再告诉它这三个长啥样，只要CNN去搜索整张图，找到了这三个特征在的地方就定位到了人脸。

 

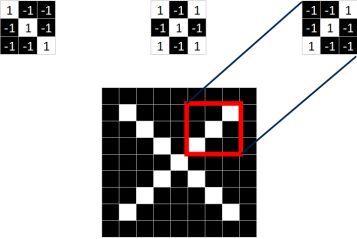
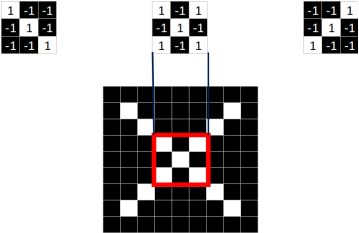
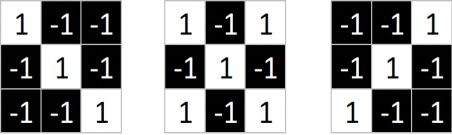
同理，从标准的X图中我们提取出三个特征（feature）

 

 

 

 

我们发现只要用这三个feature便可定位到X的某个局部。

feature在CNN中也被成为卷积核（filter），一般是3X3，或者5X5的大小。

 

【2】卷积运算

下面继续讲怎么计算。四个字：对应相乘。

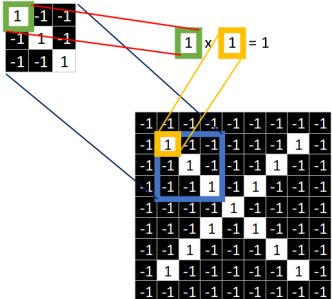
看下图。

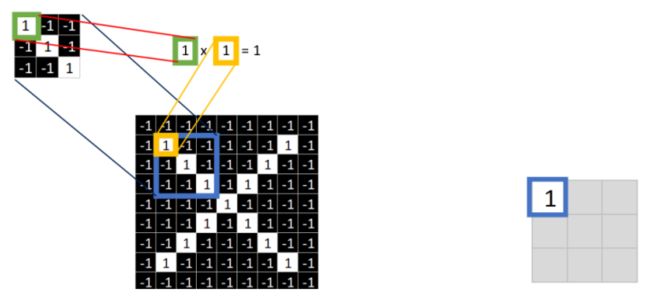
取 feature里的（1，1）元素值，再取图像上蓝色框内的（1，1）元素值，二者相乘等于1。把这个结果1填入新的图中。

 

 

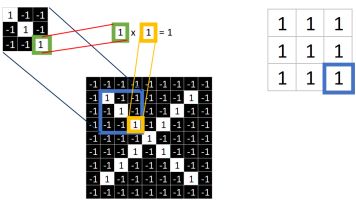
同理再继续计算其他8个坐标处的值

 

9个都计算完了就会变成这样。

 

 

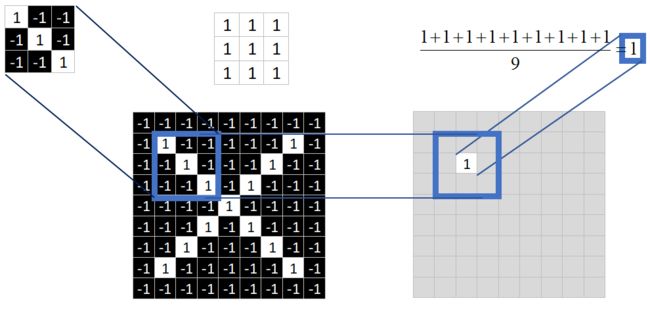
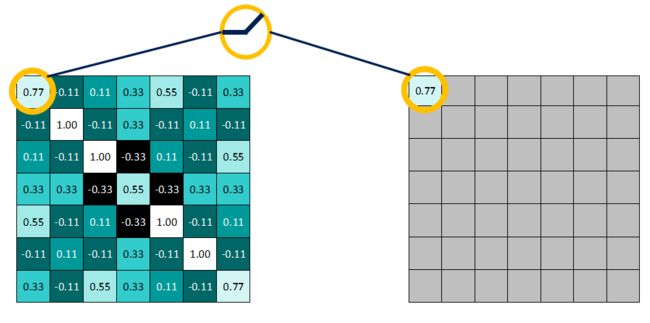
接下来的工作是对右图九个值求平均，得到一个均值，将均值填入一张新的图中。

这张新的图我们称之为 feature map （特征图）

 

 

可能有小盆友要举手问了，为什么蓝色框要放在图中这个位置呢？

这只是个栗子嘛。 这个蓝色框我们称之为 “窗口”，窗口的特性呢，就是要会滑动。

其实最开始，它应该在起始位置。

 

 

进行卷积对应相乘运算并求得均值后，滑动窗便开始向右边滑动。根据步长的不同选择滑动幅度。

比如，若 步长 stride=1，就往右平移一个像素。

 

若 步长 stride=2，就往右平移两个像素。

 

就这么移动到最右边后，返回左边，开始第二排。同样，若步长stride=1，向下平移一个像素；stride=2则向下平移2个像素。

 

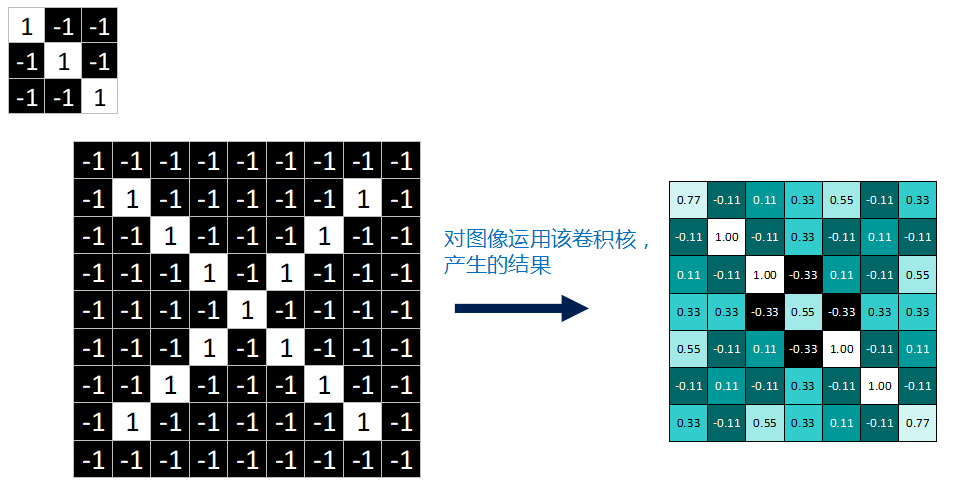
好了,经过一系列卷积对应相乘，求均值运算后，我们终于把一张完整的feature map填满了。

 

feature map是每一个feature从原始图像中提取出来的“特征”。其中的值，越接近为1表示对应位置和feature的匹配越完整，越是接近-1，表示对应位置和feature的反面匹配越完整，而值接近0的表示对应位置没有任何匹配或者说没有什么关联。

 

一个feature作用于图片产生一张feature map，对这张X图来说，我们用的是3个feature，因此最终产生3个 feature map。

 

至此，卷积运算的部分就讲完啦！~

 

【3】非线性激活层

卷积层对原图运算多个卷积产生一组线性激活响应，而非线性激活层是对之前的结果进行一个非线性的激活响应。

在神经网络中用到最多的非线性激活函数是Relu函数，它的公式定义如下：

f(x)=max(0,x)

即，保留大于等于0的值，其余所有小于0的数值直接改写为0。

为什么要这么做呢？上面说到，卷积后产生的特征图中的值，越靠近1表示与该特征越关联，越靠近-1表示越不关联，而我们进行特征提取时，为了使得数据更少，操作更方便，就直接舍弃掉那些不相关联的数据。

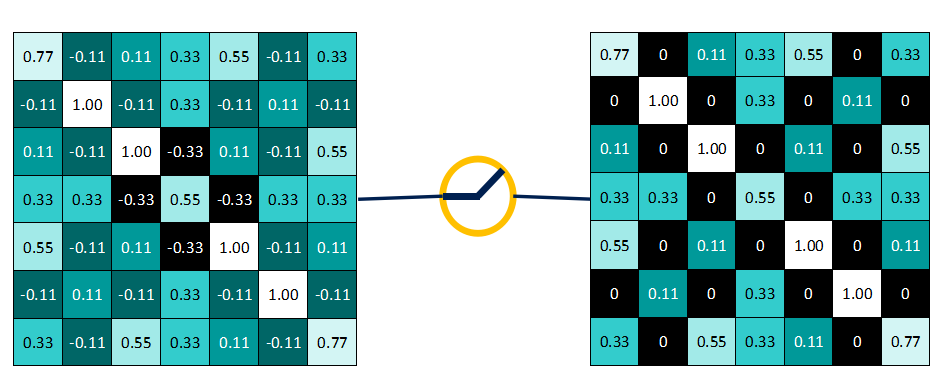
如下图所示：>=0的值不变

 

而<0的值一律改写为0

 

得到非线性激活函数作用后 的结果：

 

 

【4】pooling池化层

卷积操作后，我们得到了一张张有着不同值的feature map，尽管数据量比原图少了很多，但还是过于庞大（比较深度学习动不动就几十万张训练图片），因此接下来的池化操作就可以发挥作用了，它最大的目标就是减少数据量。

池化分为两种，Max Pooling 最大池化、Average Pooling平均池化。顾名思义，最大池化就是取最大值，平均池化就是取平均值。

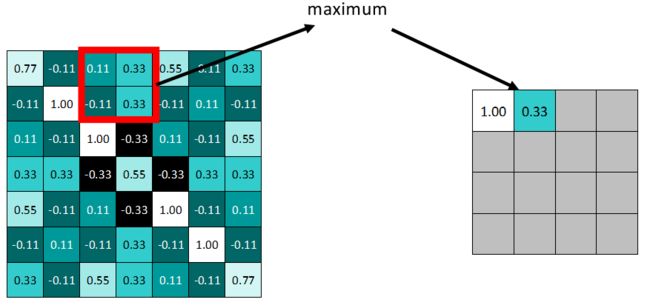
拿最大池化举例：选择池化尺寸为2x2，因为选定一个2x2的窗口，在其内选出最大值更新进新的feature map。

 

同样向右依据步长滑动窗口。

 

 

最终得到池化后的feature map。可明显发现数据量减少了很多。

因为最大池化保留了每一个小块内的最大值，所以它相当于保留了这一块最佳匹配结果（因为值越接近1表示匹配越好）。这也就意味着它不会具体关注窗口内到底是哪一个地方匹配了，而只关注是不是有某个地方匹配上了。这也就能够看出，CNN能够发现图像中是否具有某种特征，而不用在意到底在哪里具有这种特征。这也就能够帮助解决之前提到的计算机逐一像素匹配的死板做法。

 

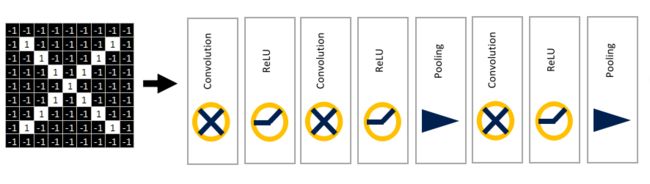
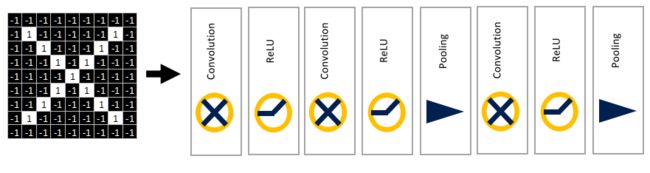
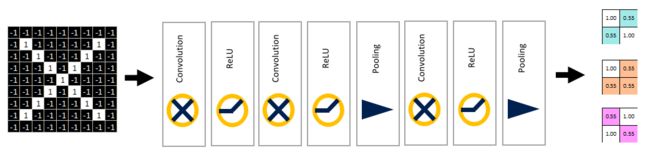
到这里就介绍了CNN的基本配置---卷积层、Relu层、池化层。

在常见的几种CNN中，这三层都是可以堆叠使用的，将前一层的输入作为后一层的输出。比如：

 

也可以自行添加更多的层以实现更为复杂的神经网络。

【5】全连接层

全连接层的形式和前馈神经网络（feedforward neural network）的形式一样，或者称为多层感知机（multilayer perceptron，MLP），纠结了很久要不要再具体介绍前馈神经网络，最终决定还是先假设读者朋友都已经有了这方面相关的知识，如果有需要的话我再单独写一篇文章介绍FNN。

还是回到上面识别图片X的栗子。

 

原图片尺寸为9X9，在一系列的卷积、relu、池化操作后，得到尺寸被压缩为2X2的三张特征图。

 

从9X9，到2X2，看起来我们已经做了很多事情了哎！似乎胜利就在前方啦(ง •_•)ง

等一下，想想我们最初和最终的目的到底是什么？是对这张照片进行识别，识别它到底是X还是O呢（其实也算是对它进行一个二分类）。那我们现在得到的是什么？是一个2X2的矩阵，好像和分类并没有什么毛线关系啊。

别急。

全连接层要做的，就是对之前的所有操作进行一个总结，给我们一个最终的结果。

它最大的目的是对特征图进行维度上的改变，来得到每个分类类别对应的概率值。

全连接层，顾名思义就是全部都连接起来，让我们把它与卷积层对比起来看。

这么说来的话前面的卷积层肯定就不是全连接了，没错，卷积层采用的是“局部连接”的思想，回忆一下卷积层的操作，是用一个3X3的图与原图进行连接操作，很明显原图中只有一个3X3的窗口能够与它连接起来。

 

 

那除窗口之外的、未连接的部分怎么办呢？ 我们都知道，采用的是将窗口滑动起来的方法后续进行连接。这个方法的思想就是“参数共享” ，参数指的就是filter，用滑动窗口的方式，将这个filter值共享给原图中的每一块区域连接进行卷积运算。

敲一下黑板：局部连接与参数共享是卷积神经网络最重要的两个性质！

那么接下来再来看全连接神经网络。

还是拿9X9的输入原图做栗子，要进行全连接的话，那权值参数矩阵应该也是9x9才对，保证每一个值都有对应的权值参数来运算。（二者坐标直接一一对应）

 

 

推荐大家直接去了解全连接神经网络（后面再详细补充）

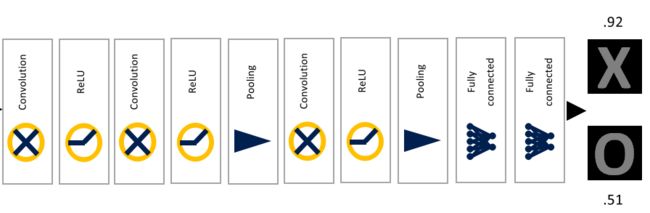
还是回来看接下来的操作，得到了2X2的特征图后，对其应用全连接网络，再全连接层中有一个非常重要的函数----Softmax，它是一个分类函数，输出的是每个对应类别的概率值。比如：

【0.5，0.03，0.89，0.97，0.42，0.15】就表示有6个类别，并且属于第四个类别的概率值0.89最大，因此判定属于第四个类别。

注意:本例中因为只有两个类别X和O，而且数据量到此已经非常少了，因此直接将三个特征图改变维度直接变成一维的数据。（相当于全连接层的每个参数均为1）

 

展开的数据即为属于类别X的概率值，值大小也在对应X的线条粗细中表现出来了。

以上所有的操作都是对标准的原图X来进行的，因此最终分类显示即为X毋庸置疑。

 

假设对一张看起来并不标准的图进行分类。如下

 

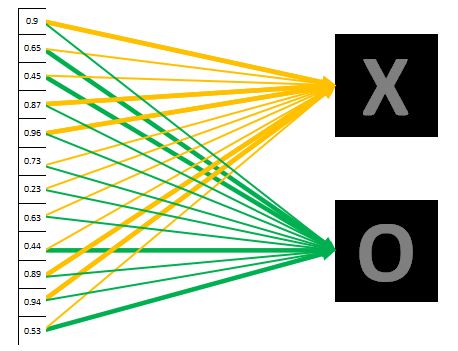
对于进行一系列操作后，假设得到的概率值如下所示：

 

0.9表示极其大可能是X，因此对应到X的黄色线条比对应到O的绿色线条要粗很多很多。

我们对结果进行统计分析后可判断这张图片里的字母为X。

 

 

【6】神经网络的训练与优化

 

前面说了那么多，其实只是一个大致的框架的设计而已，里面的参数具体是多少则是需要训练的。

那么神经网络到底需要训练什么呢？

训练的就是那些卷积核（filter）。

针对这个识别X的例子，我们可以人为定义三个3X3的卷积核，便可实现对X的特征提取。但是在实际运用中，比如识别手写字母，几乎不可能存在标准的写法，每个人的字迹都完全不同，因此原来的那三个标准的卷积核就变得不再适用了，为了提高CNN模型的通用性（机器学习中的“泛化能力”），就需要对卷积核进行改写。经过成千上万的训练集来训练，每一次加入新的数据，都有可能对卷积核里的值造成影响。

那么具体的训练方法是什么呢？

就是赫赫有名的BP算法---BackProp反向传播算法。

在训练时，我们采用的训练数据一般都是带有标签label的图片。如果图片中的字母是X，则label=x，如果图片中的字母是A，则label=A。 标签能直观地反映图片。

在最开始，训练前，我们定义一个大小为3X3的卷积核，那么里面具体的值是多少，我们都不知道，但又不能为0吧，所以就用随机初始化法来进行赋值，卷积核获取到了一个随机值，便可以开始工作。

卷积神经网络便可以开始工作了，输入一张带有标签的图片（假设图片内容是字母X）。经网络识别后判断是X的概率为0.3。本来应该是1.0的概率，现在只有0.3，问题就很明显了，存在了很大的误差。

一种简单定义误差error的计算公式为 

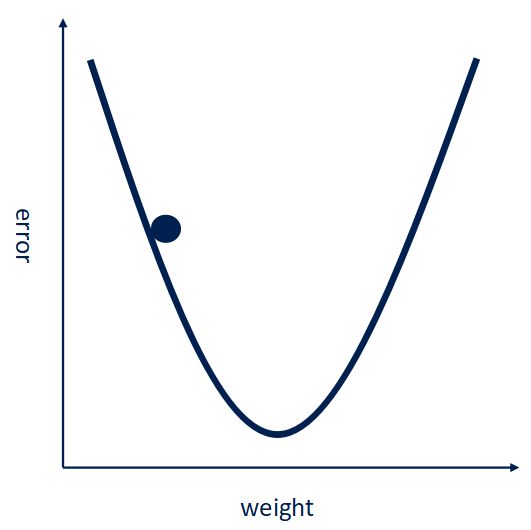
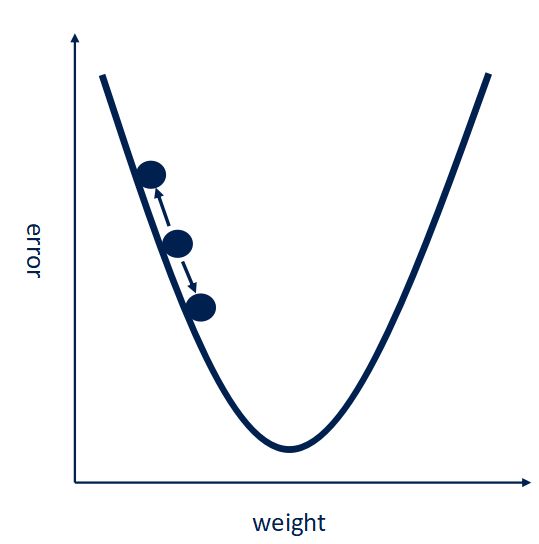
训练的终极目的就是使得这个误差最小，常用的方法是 梯度下降法。

内部设计的具体复杂公式在此不多做叙述。

简单的说可以参照下图，要使得误差error最小，就是让卷积核里的参数w往梯度下降最小的反向改变。

 

 

 

用这种方法来改变卷积核里的参数W使得误差最小。

在现有的各大深度学习框架中，CNN的优化可直接通过定义优化器解决，因此这里只是简单叙述原理以供了解。

文章转自：https://zhuanlan.zhihu.com/p/27908027 并对内容部分修改，有空再进行完善，纯粹作为好文章的收藏，作为学习记录，这篇文章很浅显地讲述了卷积神经网络的思想，值得收藏