二叉树题目:填充每个结点的下一个右侧结点指针
文章目录
- 题目
-
- 标题和出处
- 难度
- 题目描述
-
- 要求
- 示例
- 数据范围
- 进阶
- 解法一
-
- 思路和算法
- 代码
- 复杂度分析
- 解法二
-
- 思路和算法
- 代码
- 复杂度分析
- 解法三
-
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:填充每个结点的下一个右侧结点指针
出处:116. 填充每个结点的下一个右侧结点指针
难度
4 级
题目描述
要求
给定一个完美二叉树,其所有叶结点都在同一层,每个父结点都有两个子结点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next \texttt{next} next 指针,让这个指针指向其下一个右侧结点。如果找不到下一个右侧结点,则将 next \texttt{next} next 指针设置为 NULL \texttt{NULL} NULL。
初始状态下,所有 next \texttt{next} next 指针都被设置为 NULL \texttt{NULL} NULL。
示例
示例 1:
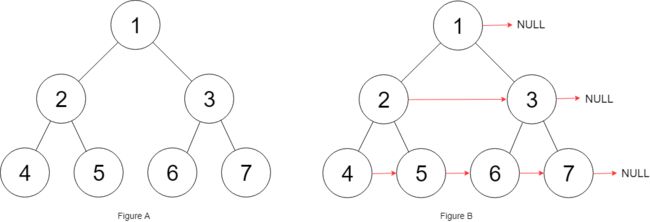
输入: root = [1,2,3,4,5,6,7] \texttt{root = [1,2,3,4,5,6,7]} root = [1,2,3,4,5,6,7]
输出: [1,#,2,3,#,4,5,6,7,#] \texttt{[1,\#,2,3,\#,4,5,6,7,\#]} [1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next \texttt{next} next 指针,以指向其下一个右侧结点,如图 B 所示。序列化的输出按层序遍历排列,同一层结点由 next \texttt{next} next 指针连接, ‘#’ \texttt{`\#'} ‘#’ 标志着每一层的结束。
示例 2:
输入: root = [] \texttt{root = []} root = []
输出: [] \texttt{[]} []
数据范围
- 树中结点数目在范围 [0, 2 12 - 1] \texttt{[0, 2}^\texttt{12}\texttt{ - 1]} [0, 212 - 1] 内
- -1000 ≤ Node.val ≤ 1000 \texttt{-1000} \le \texttt{Node.val} \le \texttt{1000} -1000≤Node.val≤1000
进阶
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不计入额外的空间。
解法一
思路和算法
由于每个结点的下一个右侧结点一定和该结点位于同一层,因此只要在同一层的结点之间填充下一个右侧结点指针即可。可以使用层序遍历实现。
层序遍历的方法为从根结点开始依次遍历每一层的结点,同一层的结点的遍历顺序为从左到右。在层序遍历的过程中需要区分不同结点所在的层,确保每一轮访问的结点为同一层的全部结点。
使用队列存储待访问的结点,初始时将根结点入队列。每一轮访问结点之前首先得到队列内的元素个数,然后访问这些结点,并将这些结点的非空子结点入队列。该做法可以确保每一轮访问的结点为同一层的全部结点。
每次访问结点时,将待访问的结点出队列。如果当前访问的结点不是当前层的最后一个结点,则此时的队首元素即为当前结点的下一个右侧结点(注意当前结点已经出队列),将当前结点的下一个右侧结点指针指向队首元素。
遍历结束之后返回根结点,此时二叉树中每个结点的下一个右侧结点指针都被填充。
代码
class Solution {
public Node connect(Node root) {
if (root == null) {
return root;
}
Queue<Node> queue = new ArrayDeque<Node>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
Node node = queue.poll();
if (i < size - 1) {
node.next = queue.peek();
}
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
return root;
}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是队列空间,队列内元素个数不超过 n n n。
解法二
思路和算法
也可以使用深度优先搜索填充每个结点的下一个右侧结点指针。具体做法是使用前序遍历,依次访问二叉树的根结点、左子树和右子树,由于前序遍历满足同一层结点被访问的顺序为从左到右,因此可以在前序遍历过程中填充每个结点的下一个右侧结点指针。由于每个结点的下一个右侧结点一定和该结点位于同一层,因此需要使用哈希表存储每一层对应的已经访问过的的最右侧结点。
前序遍历过程中,对于每个结点,执行如下操作。
-
如果当前结点所在层已经有被访问过的结点,则从哈希表中得到该层已经访问过的最右侧结点,并将已经访问过的最右侧结点的下一个右侧结点指针指向当前结点。如果当前结点所在层没有被访问过的结点,则跳过这一步。
-
将哈希表中当前结点所在层对应的已经访问过的最右侧结点设为当前结点。
遍历结束之后返回根结点,此时二叉树中每个结点的下一个右侧结点指针都被填充。
代码
class Solution {
public Node connect(Node root) {
Map<Integer, Node> rightmost = new HashMap<Integer, Node>();
Deque<Node> nodeStack = new ArrayDeque<Node>();
Deque<Integer> depthStack = new ArrayDeque<Integer>();
Node node = root;
int depth = 0;
while (!nodeStack.isEmpty() || node != null) {
while (node != null) {
if (rightmost.containsKey(depth)) {
rightmost.get(depth).next = node;
}
rightmost.put(depth, node);
nodeStack.push(node);
depthStack.push(depth);
node = node.left;
depth++;
}
node = nodeStack.pop().right;
depth = depthStack.pop() + 1;
}
return root;
}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是哈希表和栈空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。
解法三
思路和算法
为了将空间复杂度降到 O ( 1 ) O(1) O(1),需要使用其他方法遍历二叉树并填充每个结点的下一个右侧结点指针。
由于给定的二叉树是完美二叉树,所有的叶结点都在同一层,因此给定的二叉树是满二叉树,除了最深的层是叶结点以外,其余所有结点都有两个子结点。
对于满二叉树,每个结点的下一个右侧结点指针可能有以下两种情况。
-
对于同一个父结点的两个子结点,左子结点的下一个右侧结点指针指向右子结点。
-
对于同一层的两个相邻的父结点,左侧父结点的右子结点的下一个右侧结点指针指向右侧父结点的左子结点。
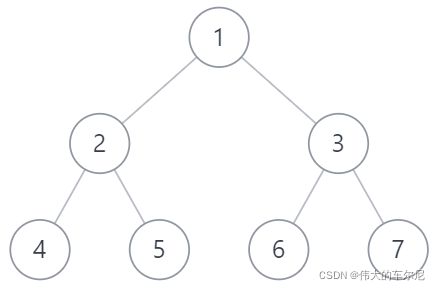
考虑如下二叉树。
结点 2 2 2 和 3 3 3 位于同一层,需要填充下一个右侧结点指针;结点 4 4 4、 5 5 5、 6 6 6 和 7 7 7 位于同一层,需要填充下一个右侧结点指针。
结点 2 2 2 和 3 3 3 有同一个父结点 1 1 1,结点 4 4 4 和 5 5 5 有同一个父结点 2 2 2,结点 6 6 6 和 7 7 7 有同一个父结点 3 3 3,因此 2 2 2 和 3 3 3 之间、 4 4 4 和 5 5 5 之间、 6 6 6 和 7 7 7 之间的下一个右侧结点指针都是上述第 1 种情况。
结点 5 5 5 和 6 6 6 的父结点分别是 2 2 2 和 3 3 3,是同一层的两个相邻的父结点,因此 5 5 5 和 6 6 6 之间的下一个右侧结点指针是上述第 2 种情况。
如果根结点为空或者根结点为叶结点,则不需要填充任何结点的下一个右侧结点指针,直接返回原始二叉树。以下只考虑根结点不为空且不为叶结点的情况。
规定根结点所在层是第 0 0 0 层,从根结点开始填充每一层的下一个右侧结点指针。由于根结点所在层没有其他结点,因此不需要填充根结点的下一个右侧结点指针。根结点的左子结点和右子结点符合上述第 1 种情况,将左子结点的下一个右侧结点指针指向右子结点,此时第 1 1 1 层的全部结点的下一个右侧结点指针填充完毕。
对于 k ≥ 0 k \ge 0 k≥0,当第 k k k 层的全部结点的下一个右侧结点指针填充完毕时,第 k k k 层的全部结点组成一个单向链表,每个结点的下一个右侧结点指针指向单向链表中的后一个结点。如果第 k k k 层的结点不是叶结点,则存在第 k + 1 k + 1 k+1 层结点,对第 k + 1 k + 1 k+1 层结点填充下一个右侧结点指针。从第 k k k 层的最左侧结点开始,执行如下操作。
-
对于第 k k k 层的当前结点,获得当前结点的左子结点和右子结点,将左子结点的下一个右侧结点指针指向右子结点。
-
如果第 k k k 层的当前结点的下一个右侧结点指针指向的结点不为空,即当前结点的右侧还有结点,则将当前结点的右子结点的下一个右侧结点指针指向当前结点右侧相邻结点的左子结点。
-
移动到右侧相邻结点,继续执行第 1 步和第 2 步。重复上述操作直到当前结点为空。
当遍历第 k k k 层并完成对第 k + 1 k + 1 k+1 层结点填充下一个右侧结点指针之后,遍历第 k + 1 k + 1 k+1 层并重复上述操作。当遍历到的层是叶结点所在层时,结束操作,此时所有结点的下一个右侧结点指针填充完毕。
当 k = 0 k = 0 k=0 时,根结点即为第 0 0 0 层的最左侧结点。第 k k k 层的最左侧结点的左子结点即为第 k + 1 k + 1 k+1 层的最左侧结点。利用该性质,可以快速定位到每一层的最左侧结点。
代码
class Solution {
public Node connect(Node root) {
if (root == null) {
return root;
}
Node start = root;
while (start.left != null) {
Node node = start;
while (node != null) {
node.left.next = node.right;
if (node.next != null) {
node.right.next = node.next.left;
}
node = node.next;
}
start = start.left;
}
return root;
}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( 1 ) O(1) O(1)。