【DL】关于tensor（张量）的介绍和理解

1. 前言

在深度学习中，我们肯定会遇到一个名词：张量（tensor）。对于一维、二维我们比较好理解，但是三维、四维、…、n维，我们该如何理解呢？下面我们将以pytorch深度学习框架为例进行详细介绍。

2. 一维

import torch # 版本：1.8.0+cpu
a = torch.tensor([1,2,3,4])
print(a)
print(a.shape)

输出：

tensor([1, 2, 3, 4])
torch.Size([4])

输出只有一个维度，所以是一维。

3. 二维

import torch # 版本：1.8.0+cpu
a = torch.tensor([[1,2,3,4]])
print(a)
print(a.shape)

输出：

tensor([[1, 2, 3, 4]])
torch.Size([1, 4])

上面输出有行和列，所以它二维张量，实际上就是一个二维矩阵。

4. 三维

import torch # 版本：1.8.0+cpu
a = torch.ones(1,3,3)
print(a)
print(a.shape)

输出：

tensor([[[1., 1., 1.],
         [1., 1., 1.],
         [1., 1., 1.]]])
torch.Size([1, 3, 3])

从输出结果可以看到这个张量是有三个维度的，前面多了一个维度1。但无法直观看到这个1体现在哪里。下面再来看一个张量，直观感受一下这个最前面的维度体现在哪里：

import torch # 版本：1.8.0+cpu
a = torch.ones(3,4,5)
print(a)
print(a.shape)

输出：

tensor([[[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]],

        [[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]],

        [[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]]])
torch.Size([3, 4, 5])

从上面输出结果，可以直观感受到最前面维度（数字3）的体现；
第一个数字3：分成3大行
第二个数字4：每一大行分为4小行
第三个数字5：每一大行分为5小列
所以数据的维度是3×4×5，最后一个数字表示列的维度；我们也可以理解为3个4行5列的数据。

如果我们将上面的张量类比为一张RGB的图像，数字3表示3个通道，每个通道的大小为4行5列。

5. 四维

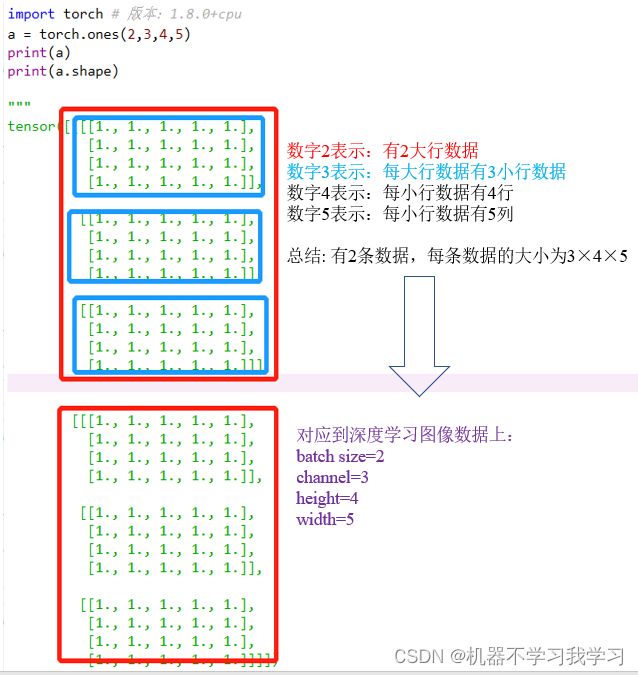
import torch # 版本：1.8.0+cpu
a = torch.ones(2,3,4,5)
print(a)
print(a.shape)

输出：

tensor([[[[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]],

         [[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]],

         [[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]]],


        [[[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]],

         [[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]],

         [[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]]]])
torch.Size([2, 3, 4, 5])

我们用分割线将上面的输出分开：

红线上面一部分是一个“维度”，下面又是一个“维度”，所以是两个维度。
再直白一点，就是张量a，有2大行，每大行又分了3小行，每行又分了4行，然后又分了5列。

张量a在日常图像数据集中可以这么理解：
第一个数字2：其实就是batchsize，就相当于这个张量是输入了2张图像
第二个数字3：每张图像的通道数是3
第三个数字4：图像的高为4
第四个数字5：图像的宽为5

参考：
https://mp.weixin.qq.com/s/9gdoufWGE8xOvwPvAcVEGw
https://blog.csdn.net/z240626191s/article/details/124204965