莫比乌斯反演

莫比乌斯反演

定义

莫比乌斯反演公式：$[n=1]=\sum _{d|n}\mu (d)$

其他几种莫比乌斯反演的形式：

标准形式：$f(n)=\sum _{d|n}g(d)\iff g(n)=\sum _{d|n}\mu (d)f(\frac{n}{d})$，所以有一种莫反的方法是设函数。

狄利克雷卷积形式：$f=g\ast 1\iff g=f\ast \mu$

现在给出莫比乌斯反演公式的证明：

对于$n=1$，显然公式成立。

对于$n\ne 1$，设$n^{\prime }$为$n$的所有不同质因子的连乘积。
形式化的说，有$n$的标准分解式：$n=\stackrel{s}{\prod _{i=1}}{p}_i^{a_i}(p_{i-1}<p_i)$，则$n^{\prime }=\stackrel{s}{\prod _{i=1}}{p}_i(p_{i-1}<p_i)$。

显然$\sum _{d|n}\mu (d)=\sum _{d|n^{\prime }}\mu (d)$，因为一旦$d$包含相同质因子，则$\mu (d)=0$。

此时，假设从$n^{\prime }$中选出具有$i$个质因子的约数$d$，则情况数共有$\left(\begin{array}{c}s\\ i\end{array}\right)$种，此时的莫比乌斯函数值是$(-1{)}^i$，对答案做的贡献就是$(-1{)}^i\left(\begin{array}{c}s\\ i\end{array}\right)$。枚举$d$的质因子数目，就得到了总的贡献：$\stackrel{s}{\sum _{i=0}}(-1{)}^i\left(\begin{array}{c}s\\ i\end{array}\right)$

应用二项式定理：
$\sum _{d|n}\mu (d)=\sum _{d|n^{\prime }}\mu (d)=\stackrel{s}{\sum _{i=0}}(-1{)}^i\left(\begin{array}{c}s\\ i\end{array}\right)=(1-1{)}^s$

因此，若$n\ne 1$，则$s\ge 1$，此式为$0$。

QED.

对于标准形式和狄利克雷卷积形式的证明，参照狄利克雷卷积。

简单莫比乌斯反演

题目要求：
$\stackrel{a}{\sum _{i=1}}\stackrel{b}{\sum _{j=1}}[\gcd (i,j)=d]$

由于个人习惯，替换一下符号，设$n\le m$。
$\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}[\gcd (i,j)=g]$

做和式的变换：

替换指标变量，同时改变枚举范围：
$\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}[\gcd (i,j)=g]=\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}[\gcd (i,j)=1]$

带入莫比乌斯反演公式：
$=\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}\sum _{d|\gcd (i,j)}\mu (d)$

替换条件式：
$=\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}\stackrel{n}{\sum _{d=1}}[d|i][d|j]\mu (d)$

分离变量：
$=\stackrel{n}{\sum _{d=1}}\mu (d)\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}[d|i]\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}[d|j]$

注意到有：$\stackrel{n}{\sum _{i=1}}[d|i]=\lfloor \frac{n}{d}\rfloor$，因此：

$=\stackrel{n}{\sum _{d=1}}\mu (d)\lfloor \frac{n}{dg}\rfloor \lfloor \frac{m}{dg}\rfloor$

于是可以整除分块。

#include
#include
using namespace std;
bool vis[50005];
vector<int> sta;
int mu[50005],pre[50005];
void Euler() {
	mu[1]=1;
	for(int i=2;i<=50000;i++) {
		if(!vis[i])
			sta.push_back(i),mu[i]=-1;
		for(auto&j:sta) {
			if(i*j>50000) break;
			int m=i*j;
			vis[m]=true;
			if(i%j) mu[m]=-mu[i];
			else break;
		}
	}
}
inline int sum(int l,int r) {
	return pre[r]-pre[l-1];
}
int calc(int n,int m) {
	int ans=0;
	for(int l=1,r;l<=n;l=r+1) 
		r=min(n/(n/l),m/(m/l)),
		ans+=(n/l)*(m/l)*sum(l,r);
	return ans;
}
int main() {
	Euler();
	for(int i=1;i<=50000;i++) pre[i]=pre[i-1]+mu[i];
//	for(int i=1;i<=10;i++)
//		cout<
	int T;
	cin>>T;
	while(T--) {
		int a,b,d;
		cin>>a>>b>>d;
		if(a>b) swap(a,b);
		cout<<calc(a/d,b/d)<<endl;
	}
}

莫比乌斯反演技巧

假设n$\le m\le K$

枚举倍数与换元

题目要求：
$\sum _{p\in \mathbb{P}}\stackrel{N}{\sum _{i=1}}\stackrel{M}{\sum _{j=1}}[\gcd (i,j)=p]$

改一下字母：
$\sum _{p\in \mathbb{P}}\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}[\gcd (i,j)=p]$

替换指标变量：
$=\sum _{p\in \mathbb{P}}\stackrel{\lfloor \frac{n}{p}\rfloor }{\sum _{i=1}}\stackrel{\lfloor \frac{m}{p}\rfloor }{\sum _{j=1}}[\gcd (i,j)=1]$
枚举上界和变量有关，一看就不是什么好事。…但是暂时替换不了。

带入反演公式：
$=\sum _{p\in \mathbb{P}}\stackrel{\lfloor \frac{n}{p}\rfloor }{\sum _{i=1}}\stackrel{\lfloor \frac{m}{p}\rfloor }{\sum _{j=1}}\sum _{d|\gcd (i,j)}\mu (d)$

替换条件式：
$=\sum _{p\in \mathbb{P}}\stackrel{\lfloor \frac{n}{p}\rfloor }{\sum _{i=1}}\stackrel{\lfloor \frac{m}{p}\rfloor }{\sum _{j=1}}\stackrel{\lfloor \frac{n}{p}\rfloor }{\sum _{d=1}}[d|i][d|j]\mu (d)$

事实上枚举范围还可以扩大：
$=\sum _{p\in \mathbb{P}}\stackrel{\lfloor \frac{n}{p}\rfloor }{\sum _{i=1}}\stackrel{\lfloor \frac{m}{p}\rfloor }{\sum _{j=1}}\stackrel{n}{\sum _{d=1}}[d|i][d|j]\mu (d)$
这样最后一个和式的枚举范围就和变量无关了。

改变求和次序，分离变量：
$=\stackrel{n}{\sum _{d=1}}\mu (d)\sum _{p\in \mathbb{P}}\stackrel{\lfloor \frac{n}{p}\rfloor }{\sum _{i=1}}[d|i]\stackrel{\lfloor \frac{m}{p}\rfloor }{\sum _{j=1}}[d|j]$

则有：
$=\stackrel{n}{\sum _{d=1}}\mu (d)\sum _{p\in \mathbb{P}}\lfloor \frac{n}{d\cdot p}\rfloor \lfloor \frac{m}{d\cdot p}\rfloor$

1. 换元，令$T=d\cdot p$，注意到$\lfloor \frac{n}{T}\rfloor$，因此$T\le n$：
   $=\stackrel{n}{\sum _{T=1}}\lfloor \frac{n}{T}\rfloor \lfloor \frac{m}{T}\rfloor \stackrel{n}{\sum _{d=1}}[d|T]\mu (d)[\frac{T}{d}\in \mathbb{P}]$
   似乎无法可想？

2. 换元，令$T=d\cdot p$，注意到$\lfloor \frac{n}{T}\rfloor$，因此$T\le n$：

$=\stackrel{n}{\sum _{T=1}}\lfloor \frac{n}{T}\rfloor \lfloor \frac{m}{T}\rfloor \sum _{p\in \mathbb{P}}[p|T]\mu (\frac{T}{p})$
这个形式看起来很是很不可做？事实上我们仔细观察右边，已经可做了。

设函数$F(x)=\sum _{p\in \mathbb{P}}[p|x]\mu \left(\frac{x}{p}\right)$，我们注意到，$p$是固定的一些数，而$p$只对它的倍数做贡献，因而我们枚举$p$，枚举$p$的倍数，要枚举的次数是$O\left(\sum _{p\in \mathbb{P}}\frac{n}{p}\right)$，根据埃氏筛时间复杂度的证明，$O\left(\sum _{p\in \mathbb{P}}\frac{n}{p}\right)=O(n\ln \ln n)$。

可以通过该题。

#include
#include
using namespace std;
const int N=1e7;
bool vis[N+5];
vector<int> sta;
int mu[N+5];
long long f[N+5],pre[N+5];
void Euler() {
	mu[1]=1;
	for(int i=2;i<=N;i++) {
		if(!vis[i])
			sta.push_back(i),mu[i]=-1;
		for(auto&j:sta) {
			if(i*j>N) break;
			int m=i*j;
			vis[m]=true;
			if(i%j) mu[m]=-mu[i];
			else break;
		}
	}
	for(auto&j:sta)
		for(int i=j;i<=N;i+=j)
			f[i]+=mu[i/j];
	for(int i=1;i<=N;i++)
		pre[i]=pre[i-1]+f[i];
}
long long calc(int n,int m) {
	long long ans=0;
	for(int l=1,r;l<=n;l=r+1)
		r=min(n/(n/l),m/(m/l)),
		ans+=(pre[r]-pre[l-1])*(n/l)*(m/l);
	return ans;
}
int main() {
	Euler();
	int T;
	cin>>T;
	while(T--) {
		int n,m;
		cin>>n>>m;
		if(n>m) swap(n,m);
		cout<<calc(n,m)<<endl;
	}
}

其实第一种换元也是可以做的，只需要枚举$d$的质数倍就好了。其实换元只是为了看起来清晰一点。

容斥

大矩形表示$(b,d)$范围内的答案，再减去绿色、橙色范围内的答案，最后加上紫色的答案，就得到了红色阴影部分的答案，也就是要求的答案。因此做一个二维容斥。

#include
#include
using namespace std;
bool vis[50005];
vector<int> sta;
int mu[50005],pre[50005];
void Euler() {
	mu[1]=1;
	for(int i=2;i<=50000;i++) {
		if(!vis[i])
			sta.push_back(i),mu[i]=-1;
		for(auto&j:sta) {
			if(i*j>50000) break;
			int m=i*j;
			vis[m]=true;
			if(i%j) mu[m]=-mu[i];
			else break;
		}
	}
}
inline int sum(int l,int r) {
	return pre[r]-pre[l-1];
}
int calc(int n,int m) {
	if(n>m) swap(n,m);
	int ans=0;
	for(int l=1,r;l<=n;l=r+1) 
		r=min(n/(n/l),m/(m/l)),
		ans+=(n/l)*(m/l)*sum(l,r);
	return ans;
}
int main() {
	Euler();
	for(int i=1;i<=50000;i++) pre[i]=pre[i-1]+mu[i];
//	for(int i=1;i<=10;i++)
//		cout<
	int T;
	cin>>T;
	while(T--) {
		int a,b,c,d,k;
		cin>>a>>b>>c>>d>>k;
		cout<<calc(b/k,d/k)-calc((a-1)/k,d/k)-calc(b/k,(c-1)/k)+calc((a-1)/k,(c-1)/k)<<endl;
	}
}

约数个数函数（一）

题目要求：
$\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}d(i\cdot j)$

其中$d$表述约数个数函数。

事实上必须知道约数个数函数有性质：
$d(i\cdot j)=\sum _{x|i}\sum _{y|j}[x\perp y]$

这里贴出证明：
让大家喜闻乐见的证明（推荐）
接近本质的证明（不完善，不推荐）

因此可以反演：
$\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}d(i\cdot j)$
$=\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}\sum _{x|i}\sum _{y|j}[x\perp y]$
$=\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}\stackrel{n}{\sum _{x=1}}[x|i]\stackrel{m}{\sum _{y=1}}[y|j][x\perp y]$
$=\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}\stackrel{n}{\sum _{x=1}}[x|i]\stackrel{m}{\sum _{y=1}}[y|j]\stackrel{n}{\sum _{d=1}}[d|x][d|y]\mu (d)$
$=\stackrel{n}{\sum _{d=1}}\mu (d)\stackrel{n}{\sum _{x=1}}[d|x]\stackrel{m}{\sum _{y=1}}[d|y]\stackrel{n}{\sum _{i=1}}[x|i]\stackrel{m}{\sum _{j=1}}[y|j]$
$=\stackrel{n}{\sum _{d=1}}\mu (d)\stackrel{n}{\sum _{x=1}}[d|x]\lfloor \frac{n}{x}\rfloor \stackrel{m}{\sum _{y=1}}[d|y]\lfloor \frac{n}{y}\rfloor$

注意到此时已经无法直接把$x,y$化掉了，因为$x,y$不仅缀有艾弗森括号，还有其他式子。此时我们直接令$x=d\cdot x,y=d\cdot y$，另外注意到此时我们的枚举上界是可以不变的，因为一旦$dx>n$，则和式的值为$0$，因此没必要做限制（虽然本题不影响）：
$=\stackrel{n}{\sum _{d=1}}\mu (d)\stackrel{n}{\sum _{x=1}}\lfloor \frac{n}{dx}\rfloor \stackrel{m}{\sum _{y=1}}\lfloor \frac{m}{dy}\rfloor$

发现已经可做了，因为整除定理表明$\lfloor \frac{a}{bc}\rfloor =\lfloor \frac{\lfloor \frac{a}{b}\rfloor }{c}\rfloor$：
设$F(x)=\stackrel{x}{\sum _{i=1}}\lfloor \frac{x}{i}\rfloor$，$F(x)$可以直接$O(n\sqrt{n})$预处理出来，这已经可以做了。当然事实上，接下来你会看到，这个东西可以$O(n)$预处理。

因此最后：
$=\stackrel{n}{\sum _{d=1}}\mu (d)F\left(\lfloor \frac{n}{d}\rfloor \right)F\left(\lfloor \frac{m}{d}\rfloor \right)$

#include
#include
using namespace std;
const int N=5e4;
bool vis[N+5];
vector<int> sta;
int mu[N+5];
long long pre[N+5];
long long F[N+5];
//F[i]表示∑x:[i/x] 
void Euler() {
	mu[1]=1;
	for(int i=2;i<=N;i++) {
		if(!vis[i])
			sta.push_back(i),mu[i]=-1;
		for(auto&j:sta) {
			if(i*j>N) break;
			int m=i*j;
			vis[m]=true;
			if(i%j) mu[m]=-mu[i];
			else break;
		}
	}
	for(int i=1;i<=N;i++) pre[i]=pre[i-1]+mu[i];
	for(int i=1;i<=N;i++)
		for(int l=1,r;l<=i;l=r+1)
			r=(i/(i/l)),
			F[i]+=(long long)(i/l)*(r-l+1);
}
long long calc(int n,int m) {
	long long ans=0;
	for(int l=1,r;l<=n;l=r+1)
		r=min(n/(n/l),m/(m/l)),
		ans+=(pre[r]-pre[l-1])*F[n/l]*F[m/l];
	return ans;
}
int main() {
	Euler();
	int T;
	cin>>T;
	while(T--) {
		int n,m;
		cin>>n>>m;
		if(n>m) swap(n,m);
		cout<<calc(n,m)<<endl;
	}
}

枚举gcd，分块套分块，小学奥数

题目要求：
$\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}lcm(i,j)$

首先肯定把$lcm$搞成$gcd$：
$=\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}\frac{i\cdot j}{\gcd (i,j)}$

这个式子似乎已经很难做了，又没法换元，因此我们考虑直接枚举$gcd$，暴力搞一下这个式子：
$=\stackrel{n}{\sum _{g=1}}\stackrel{n}{\sum _{i=1}}\stackrel{m}{\sum _{j=1}}\frac{i\cdot j}{g}[\gcd (i,j)=g]$
$=\stackrel{n}{\sum _{g=1}}\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}i\cdot j\cdot g[\gcd (i,j)=1]$
$=\stackrel{n}{\sum _{g=1}}g\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}i\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}j[\gcd (i,j)=1]$
$=\stackrel{n}{\sum _{g=1}}g\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}i\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}j\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{d=1}}[d|i][d|j]\mu (d)$
$=\stackrel{n}{\sum _{g=1}}g\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}i\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}j\stackrel{n}{\sum _{d=1}}[d|i][d|j]\mu (d)$
$=\stackrel{n}{\sum _{d=1}}\mu (d)\stackrel{n}{\sum _{g=1}}g\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}[d|i]i\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}[d|j]j$
$=\stackrel{n}{\sum _{d=1}}\mu (d)\stackrel{n}{\sum _{g=1}}g\stackrel{\lfloor \frac{n}{dg}\rfloor }{\sum _{i=1}}i\cdot d\stackrel{\lfloor \frac{m}{dg}\rfloor }{\sum _{j=1}}j\cdot d$
$=\stackrel{n}{\sum _{d=1}}\mu (d)d^2\stackrel{n}{\sum _{g=1}}g\stackrel{\lfloor \frac{n}{dg}\rfloor }{\sum _{i=1}}i\stackrel{\lfloor \frac{m}{dg}\rfloor }{\sum _{j=1}}j$

这时候已经可以做了，不是吗？
外层对$d$分块，内层对$g$分块，分块套分块，时间复杂度$O(n)$。

最后两个和式是等差数列，平方数的和，小学奥数是可以速算的，再不济可以打表，对不对？

#include
#include
using namespace std;
const int N=1e7;
bool vis[N+5];
vector<int> sta;
int mu[N+5];
void Euler() {
	mu[1]=1;
	for(int i=2;i<=N;i++) {
		if(!vis[i])
			sta.push_back(i),mu[i]=-1;
		for(auto&j:sta) {
			if(i*j>N) break;
			int m=i*j;
			vis[m]=true;
			if(i%j) mu[m]=-mu[i];
			else break;
		}
	}
}
const long long mod=20101009;
long long f[N+5],F[N+5];
long long sum(int n,int m) {
	long long ans=0;
	for(int l=1,r;l<=n;l=r+1)
		r=min(n/(n/l),m/(m/l)),
		(ans+=((f[r]-f[l-1])%mod+mod)*f[n/l]%mod*f[m/l])%=mod;
	return ans;
}
long long calc(int n,int m) {
	long long ans=0;
	for(int l=1,r;l<=n;l=r+1)
		r=min(n/(n/l),m/(m/l)),
		(ans+=((F[r]-F[l-1])%mod+mod)*sum(n/l,m/l))%=mod;
	return ans;
}
int main() {
	int n,m;
	Euler();
	for(int i=1;i<=N;i++)
		f[i]=((long long)i*(i+1)>>1)%mod;
	for(int i=1;i<=N;i++)
		F[i]=(((long long)i*i*mu[i]+F[i-1])%mod+mod)%mod;
	cin>>n>>m;
	if(n>m) swap(n,m);
	cout<<calc(n,m);
}

后记：

当然还有一种做法是先对$g$分块，再对$d$分块，也是可以做的，不过我们能够让$d$成为分块的外层，还归功于我们扩大了枚举范围

和式与prod式的变换

题目要求：
$\stackrel{n}{\prod _{i=1}}\stackrel{m}{\prod _{j=1}}f\left(gcd(i,j)\right)$

prod式应该怎么变换的？其实与和式的变换差不多：

1. prod式满足交换律。
2. 满足结合律：$\prod _{i}f(i)\prod _{j}g(j)\prod _{k}h(k)=\prod _{i}f(i)\left(\prod _{j}g(j)\prod _{k}h(k)\right)$
3. 满足分配律：$\stackrel{n}{\prod _{i=1}}c{a}_i=c^n\stackrel{n}{\prod _{i=1}}{a}_i$
   至于加法…好像没法分配
4. 指数：${\left(\prod _{i}f(i)\prod _{j}g(j)\right)}^k={\left(\prod _{i}f(i)\right)}^k{\left(\prod _{j}g(j)\right)}^k=\prod _i{f}^k(i)\prod _j{g}^k(j)$
5. 任何大型运算符都可以替换条件式，只不过细节不同，求和符号条件式转艾弗森写在系数上：$\sum _{d|n}f(d)=\sum [d|n]f(d)$，而连乘积符号条件式转艾弗森写在指数上：$\prod _{d|n}f(d)=\prod f(d{)}^{[d|n]}$
6. 任何大型运算符都可以替换指标变量
7. 改变运算次序：$\prod _i\prod _{j}f(i)g(j)=\prod _j\prod _{i}f(i)g(j)$
8. 分离变量：$\prod _i\prod _{j}f(i)g(j)=\prod _{i}f(i)\prod _{j}g(j)$
9. 求和符号与连乘积符号：$\prod _i\prod _{j}f(i{)}^{g(j)}=\prod _{i}f(i{)}^{\sum _{j}g(j)}$
   求和符号从指数跑下来就是连乘积符号，连乘积跑到指数上就是求和。

对这个式子做一下处理：
$\stackrel{n}{\prod _{i=1}}\stackrel{m}{\prod _{j=1}}f\left(gcd(i,j)\right)$

首先发现无法可想，可暴力枚举一下$gcd$：
$=\stackrel{n}{\prod _{g=1}}\stackrel{n}{\prod _{i=1}}\stackrel{m}{\prod _{j=1}}f{\left(g\right)}^{[gcd(i,j)=g]}$
$=\stackrel{n}{\prod _{g=1}}\stackrel{\lfloor \frac{n}{g}\rfloor }{\prod _{i=1}}\stackrel{\lfloor \frac{m}{g}\rfloor }{\prod _{j=1}}f{\left(g\right)}^{[gcd(i,j)=1]}$

把$prod$式推到指数上：
$=\stackrel{n}{\prod _{g=1}}f{\left(g\right)}^{\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}\stackrel{\lfloor \frac{m}{g}\rfloor }{\sum _{j=1}}[gcd(i,j)=1]}$

对指数做一波反演…：
$=\stackrel{n}{\prod _{g=1}}f{\left(g\right)}^{\stackrel{n}{\sum _{d=1}}\mu (d)\lfloor \frac{n}{dg}\rfloor \lfloor \frac{m}{dg}\rfloor }$

似乎无法可想了，所以再把和式拉下来：
$=\stackrel{n}{\prod _{g=1}}\stackrel{n}{\prod _{d=1}}f{\left(g\right)}^{\mu (d)\lfloor \frac{n}{dg}\rfloor \lfloor \frac{m}{dg}\rfloor }$

换元，令$T=dp$：
$=\stackrel{n}{\prod _{T=1}}\stackrel{n}{\prod _{d=1}}f{\left(\frac{T}{d}\right)}^{\mu (d)[d|T]\lfloor \frac{n}{T}\rfloor \lfloor \frac{m}{T}\rfloor }$
$=\stackrel{n}{\prod _{T=1}}{\left(\stackrel{n}{\prod _{d=1}}f{\left(\frac{T}{d}\right)}^{\mu (d)[d|T]}\right)}^{\lfloor \frac{n}{T}\rfloor \lfloor \frac{m}{T}\rfloor }$

每个$d$都只对它的倍数做贡献，括号内求一个区间积，括号外面整除分块，于是就做完了。
对$g$换元当然也是可做的。

#include
#include
using namespace std;
long long pow(long long a,long long b,long long c) {
	long long ans=1;
	while(b) {
		if(b&1) ans=(ans*a)%c;
		a=(a*a)%c;
		b>>=1;
	}
	return ans;
}
const int N=1e6;
const long long M=1e9+7;
bool vis[N+5];
vector<int> sta;
int mu[N+5];
long long f[N+5],g[N+5],F[N+5];
void Euler() {
	mu[1]=1;
	for(int i=2; i<=N; i++) {
		if(!vis[i])
			sta.push_back(i),
			              mu[i]=-1;
		for(auto&j:sta) {
			if(i*j>N) break;
			int m=i*j;
			vis[m]=true;
			if(i%j) mu[m]=-mu[i];
			else break;
		}
	}
	F[0]=F[1]=f[1]=g[1]=1;
	for(int i=2; i<=N; i++)
		f[i]=(f[i-1]+f[i-2])%M,
		g[i]=pow(f[i],M-2,M),
		F[i]=1;
	for(int i=1; i<=N; i++)
		for(int j=i; j<=N;j+=i)
			if(mu[j/i])
				F[j]=F[j]*(~mu[j/i]?f[i]:g[i])%M;
	for(int i=1; i<=N; i++)
		(F[i]*=F[i-1])%=M;
}
long long calc(int n,int m) {
	long long ans=1;
	long long t;
	for(int l=1,r;l<=n;l=r+1)
		r=min(n/(n/l),m/(m/l)),
		t=F[r]*pow(F[l-1],M-2,M)%M,
		(ans*=pow(t,(long long)(n/l)*(m/l)%(M-1),M))%=M;//这里必须要括起来是因为整除
	return ans;
}
int main() {
	int n,m;
	Euler();
//	for(int i=1;i<=10;i++)
//		cout<
	int T;
	cin>>T;
	while(T--) {
		cin>>n>>m;
		if(n>m) swap(n,m);
		cout<<calc(n,m)<<endl;
	}
}

狄利克雷卷积，杜教筛

题目要求：
$\stackrel{n}{\sum _{i=1}}\stackrel{n}{\sum _{j=1}}ij\gcd (i,j)$
$=\stackrel{n}{\sum _{g=1}}g\stackrel{n}{\sum _{i=1}}i\stackrel{n}{\sum _{j=1}}j[gcd(i,j)=g]$
$=\stackrel{n}{\sum _{g=1}}{g}^3\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}i\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{j=1}}j[gcd(i,j)=1]$
$=\stackrel{n}{\sum _{d=1}}\mu (d)\stackrel{n}{\sum _{g=1}}{g}^3\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{i=1}}[d|i]i\stackrel{\lfloor \frac{n}{g}\rfloor }{\sum _{j=1}}[d|j]j$
= ∑ d = 1 n μ ( d ) ∑ g = 1 n d 2 g 3 ( ∑ i = 1 ⌊ n d g ⌋ i ) 2 =\overset{n}{\underset{d=1}\sum}\mu(d)\overset{n}{\underset{g=1}\sum}d^2g^3\left(\overset{\left\lfloor\frac n{dg}\right\rfloor}{\underset{i=1}\sum}i\right)^2 =d=1∑​n​μ(d)g=1∑​n​d2g3 ​i=1∑​⌊dgn​⌋​i ​2
换元，$T=dg$：
= ∑ T = 1 n ∑ g = 1 n g μ ( T g ) [ g ∣ T ] ( ∑ i = 1 ⌊ n T ⌋ i ) 2 =\overset{n}{\underset{T=1}\sum}\overset{n}{\underset{g=1}\sum}g\mu(\frac T g)[g|T]\left(\overset{\left\lfloor\frac n{T}\right\rfloor}{\underset{i=1}\sum}i\right)^2 =T=1∑​n​g=1∑​n​gμ(gT​)[g∣T] ​i=1∑​⌊Tn​⌋​i ​2
= ∑ T = 1 n ∑ g ∣ T μ ( T g ) g ( ∑ i = 1 ⌊ n T ⌋ i ) 2 =\overset{n}{\underset{T=1}\sum}\overset{}{\underset{g|T}\sum}\mu(\frac T g)g\left(\overset{\left\lfloor\frac n{T}\right\rfloor}{\underset{i=1}\sum}i\right)^2 =T=1∑​n​g∣T∑​​μ(gT​)g ​i=1∑​⌊Tn​⌋​i ​2
= ∑ T = 1 n ( ∑ i = 1 ⌊ n T ⌋ i ) 2 ∑ g ∣ T μ ( T g ) g =\overset{n}{\underset{T=1}\sum}\left(\overset{\left\lfloor\frac n{T}\right\rfloor}{\underset{i=1}\sum}i\right)^2\overset{}{\underset{g|T}\sum}\mu(\frac T g)g =T=1∑​n​ ​i=1∑​⌊Tn​⌋​i ​2g∣T∑​​μ(gT​)g

最后一个和式很明显是狄利克雷卷积：
= ∑ T = 1 n ( ∑ i = 1 ⌊ n T ⌋ i ) 2 φ ( T ) =\overset{n}{\underset{T=1}\sum}\left(\overset{\left\lfloor\frac n{T}\right\rfloor}{\underset{i=1}\sum}i\right)^2\varphi(T) =T=1∑​n​ ​i=1∑​⌊Tn​⌋​i ​2φ(T)

杜教筛一波就做完了…这个题好像就必须用到小学奥数了，自己看着办吧。

#include
#include
#include
using namespace std;
const int N=1e7;
long long M;
long long phi[N+5];
bool vis[N+5];
vector<int> sta;
long long pow(long long a,long long b,long long c) {
	long long ans=1;
	while(b) {
		if(b&1) ans=(ans*a)%c;
		a=(a*a)%c;
		b>>=1;
	}
	return ans;
}
void Euler() {
	phi[1]=1;
	for(int i=2;i<=N;i++) {
		if(!vis[i])
			phi[i]=i-1,
			sta.push_back(i);
		for(auto&j:sta) {
			long long m=(long long)i*j;
			if(m>N) break;
			vis[m]=true;
			if(i%j)
				phi[m]=phi[i]*phi[j];
			else {
				phi[m]=phi[i]*j;
				break;
			}
		}
	}
	for(long long i=1;i<=N;i++)
		(phi[i]=phi[i]*i%M*i%M+phi[i-1])%=M; 
}
long long inv;
long long f(long long n) {
	n%=M;
	return (n*(n+1)/2)%M*((n*(n+1)/2)%M)%M;
}
long long h(long long n) {
	n%=M;
	return n*(n+1)%M*(2*n+1)%M*inv%M;
}
//typedef long long LL;
//LL h(LL x){x%=M;return x*(x+1)%M*(2*x+1)%M*inv%M;}
//LL f(LL x){x%=M;return(x*(x+1)/2)%M*((x*(x+1)/2)%M)%M;}
unordered_map<long long,long long> H;
long long sum(long long n) {
	if(n<=N) return phi[n];
	if(H.count(n)) return H[n];
	long long ans=f(n);
	for(long long l=2,r;l<=n;l=r+1)
		r=n/(n/l),
		ans=(ans-(h(r)-h(l-1))%M*sum(n/l)%M+M)%M;
	return H[n]=ans;
}
long long calc(long long n) {
	long long ans=0;
	for(long long l=1,r;l<=n;l=r+1) 
		r=n/(n/l),
		ans=(ans+(sum(r)-sum(l-1))%M*f(n/l)%M+M)%M;
	return ans;
}
signed main() {
	long long n;
	cin>>M>>n;
	inv=pow(6,M-2,M);
//	cout<<"***"<
	Euler();
//	cout<
//	cout<
//	cout<
//	for(int i=1;i<=10;i++)
//		cout<
//	cout<
	cout<<calc(n);
}

两种换元方式都可以，用欧拉反演这道题会简单许多，上一道题用不了欧拉反演的原因就是，它把$gcd$搞到了分母上。

递推

其中$d$函数就是整除函数${\sigma }_0$.
首先注意到整除函数有如下性质：

那么我们可以替换一下题目中的式子：

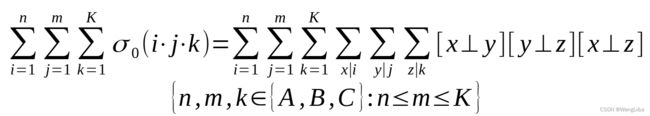
这就是一个莫反的形式，一种做法是同时对三个艾弗森括号进行莫比乌斯反演，最后枚举三元环，可以通过此题。
另一种做法是只对一个艾弗森括号进行莫比乌斯反演，这是数论做法，也可以通过此题。
这里选择对$[y\perp z]$做反演：

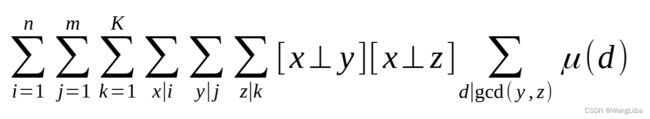
然后整理下式子：

然后在这里，一般来说是把$d$拉到最左边，不过这一次是把$x$拉到最左边，然后继续整理：

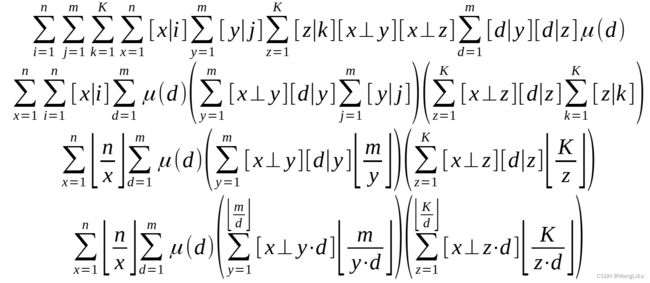
注意这里艾弗森括号可以拆开。

然后发现$[x\perp d]$这一项与后面两个和式没关系了，可以拉出来：

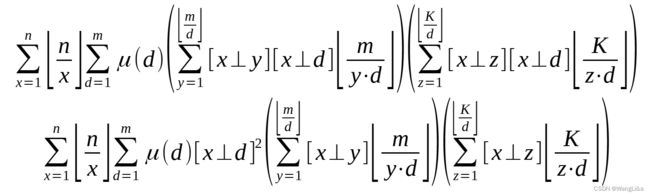
注意到艾弗森括号只有$0$或者$1$两种取值，所以平方符号可以不写：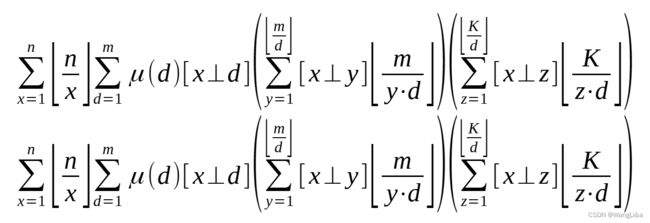
然后呢？似乎无法可想。
所以可以考虑设函数了：

这时候可以考虑数论分块了：

此时这两个函数如果暴算的话，我们枚举$x$和$d$，总复杂度就是O(n²logn)，因为$f$的$N$取值是一个调和级数。

当然还有一个神仙的做法，其实这两个函数是可以递推的：

首先假设$k$不含有任何相同质因子。也就是说$\mu (k)\ne 0$。
如果有$k^{\prime }$含有相同质因子，那么显然有对应的$k$只含有$k^{\prime }$的每个质因子一次，有$f(N,k)=f(N,k^{\prime })，g(N,k)=g(N,k^{\prime })$。因为只需要判断是否含有相同质因子，就能判断是否互质，而不关乎相同质因子数目。
那么对于上面的$k$，其实只需要做一个简单的容斥：
$f(N,k)=\stackrel{N}{\sum _{i=1}}\lfloor \frac{N}{i}\rfloor [i\perp k]$
$=\stackrel{N}{\sum _{i=1}}\lfloor \frac{N}{i}\rfloor [i\perp \frac{k}{p}]-\stackrel{N}{\sum _{i=1}}\lfloor \frac{N}{i}\rfloor [i\perp \frac{k}{p}][p|i]$
$=\stackrel{N}{\sum _{i=1}}\lfloor \frac{N}{i}\rfloor [i\perp \frac{k}{p}]-\stackrel{N}{\sum _{i=1}}\lfloor \frac{N}{i}\rfloor [i\perp \frac{k}{p}][p|i]$
$=\stackrel{N}{\sum _{i=1}}\lfloor \frac{N}{i}\rfloor [i\perp \frac{k}{p}]-\stackrel{\lfloor \frac{N}{p}\rfloor }{\sum _{i=1}}\lfloor \frac{N}{p\cdot i}\rfloor [p\cdot i\perp \frac{k}{p}]$

注意到一定有$p\perp \frac{k}{p}$，因此可以去掉：
$=\stackrel{N}{\sum _{i=1}}\lfloor \frac{N}{i}\rfloor [i\perp \frac{k}{p}]-\stackrel{\lfloor \frac{N}{p}\rfloor }{\sum _{i=1}}\lfloor \frac{N}{p\cdot i}\rfloor [i\perp \frac{k}{p}]$
$=f\left(N,\frac{k}{p}\right)-f\left(\lfloor \frac{N}{p}\rfloor ,\frac{k}{p}\right)$

对于$g$，也有类似的容斥：
$f(N,k)=\stackrel{N}{\sum _{i=1}}\mu (i)[i\perp k]$
$=\stackrel{N}{\sum _{i=1}}\mu (i)[i\perp \frac{k}{p}]-\stackrel{N}{\sum _{i=1}}\mu (i)[i\perp \frac{k}{p}][p|i]$
$=\stackrel{N}{\sum _{i=1}}\mu (i)[i\perp \frac{k}{p}]-\stackrel{\lfloor \frac{N}{p}\rfloor }{\sum _{i=1}}\mu (p\cdot i)[i\perp \frac{k}{p}]$

若$p\perp i$，则$\mu (p\cdot i)=-\mu (i)$，否则$\mu (p\cdot i)=0$：
$=\stackrel{N}{\sum _{i=1}}\mu (i)[i\perp \frac{k}{p}]+\stackrel{\lfloor \frac{N}{p}\rfloor }{\sum _{i=1}}\mu (i)[i\perp p][i\perp \frac{k}{p}]$

$i\perp p$与$i\perp \frac{k}{p}$显然可以合起来：
$=\stackrel{N}{\sum _{i=1}}\mu (i)[i\perp \frac{k}{p}]+\stackrel{\lfloor \frac{N}{p}\rfloor }{\sum _{i=1}}\mu (i)[i\perp k]$
$=g(N,\frac{k}{p})+g\left(\lfloor \frac{N}{p}\rfloor ,k\right)$

我们再回顾一下递推式：

然后是初值：

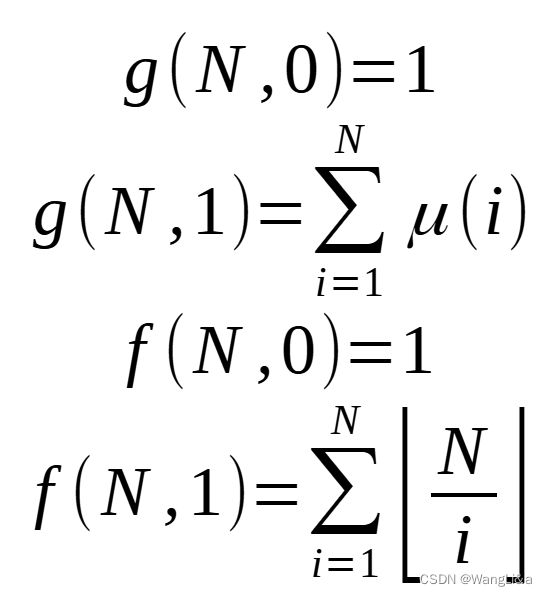
所有的$f(x,1)$的值，可以数论分块，O($N$^1.5)求出。
当然还有一种做法：

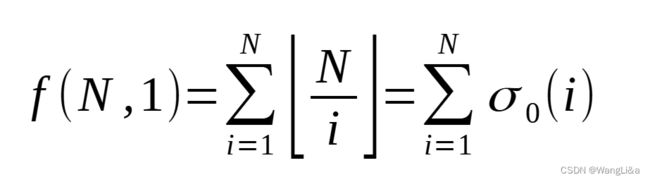
这样可以O($N$)求出所有的$f(x,1)$。
这个式子可以证明一下，从左到右证明较难，而从右到左证明较易：

因此：


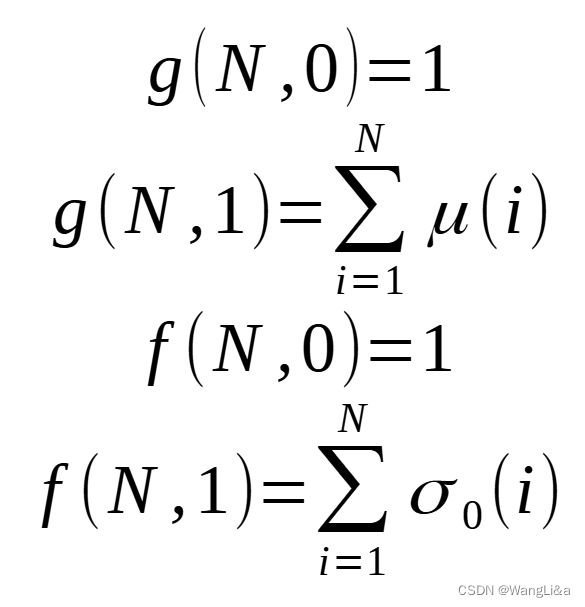
那么我们分析一下复杂度：
$f,g$的第一维，取遍$N$的取整点，复杂度为$O(\sqrt{N})$，第二维为$\mu (i)\ne 0$的数量，$N=100000$时爆搜一波有$60000$个，$O(N)$。

然后就是调用$g(l-1),g(r)$的问题，由于有$O(\sqrt{n})$个$l-1,r$，每个$l-1,r$都会对应$O(\sqrt{r})$个取整点，会不会使得复杂度增加为$O(n)$的问题。答案是不会，我们只需要讨论$r$，因为$l-1$肯定就是上一个块的$r$。我们注意到$r=n/(n/l)$，$r$本身就是$n$的取整点。

因此写了一波二维unordered_map优化整除分块，被卡成30：

#include
#include
#include
#include
using namespace std;
const int N=1e5;
const long long M=1e9+7;
vector<int> sta;
bool vis[N+5];
int mu[N+5],LPF[N+5],con[N+5],s0[N+5],LPFx[N+5],cnt[N+5];
//莫比乌斯函数，最小质因子，本质相同素数，约数个数，含有的最小质因子的次数，本质不同质因子个数 
unordered_map<int,long long> f[N+5],g[N+5];
int getf(int n,int k) {
	int p=LPF[k];
	if(!n) return 0;
	if(k==1||!k||f[n][k]) return /*cout<f[n][k];
	else return /*cout<f[n][k]=getf(n,k/p)-getf(n/p,k/p);
//	int s=cnt[k],p=LPF[k];
//	if(k==1||!k||f[s][{n,k}]) return f[s][{n,k}];
//	else return f[s][{n,k}]=getf(n,k/p)+getf(n/p,k/p);
}
int getg(int n,int k) {
	int p=LPF[k];
	if(!n) return 0;
	if(k==1||!k||g[n][k]) return /*cout<g[n][k];
	else return /*cout<g[n][k]=getg(n,k/p)+getg(n/p,k);
//	int s=cnt[k],p=LPF[k];
//	if(k==1||!k||g[s][{n,k}]) return g[s][{n,k}];
//	else return g[s][{n,k}]=getg(n,k/p)+get(n/p,k);
}
void Euler() {
	mu[1]=1;
	s0[1]=1;
	LPFx[1]=1;
	con[1]=1; 
	cnt[1]=1;
	for(int i=2;i<=N;i++) {
		if(!vis[i])
			mu[i]=-1,
			LPF[i]=i,
			con[i]=i,
			LPFx[i]=1,
			s0[i]=2,
			cnt[i]=1,
			sta.push_back(i);
		for(auto&j:sta) {
			int x=i*j;
			if(x>N) break;
			vis[x]=true;
			LPF[x]=j;
			if(i%j) 
				mu[x]=-mu[i],
				con[x]=con[i]*con[j],
				s0[x]=s0[i]*s0[j],
				LPFx[x]=1,
				cnt[x]=cnt[i]+1;
			else {
				con[x]=con[i];
				LPFx[x]=LPFx[i]+1;
				cnt[x]=cnt[i];
				s0[x]=s0[i]/LPFx[x]*(LPFx[x]+1);
				break;
			}
		}
	}
	for(int i=1;i<=N;i++) f[i][0]=g[i][0]=1;
	for(int i=1;i<=N;i++) f[i][1]=f[i-1][1]+s0[i],
						  g[i][1]=g[i-1][1]+mu[i];
}
long long calc(int n,int m,int K) {
	if(n>K) swap(n,K);
	if(n>m) swap(n,m);
	if(m>K) swap(m,K);
	long long sum=0;
	for(long long x=1;x<=n;x++) {
		long long sumx=0;
		for(long long l=1,r;l<=m;l=r+1) 
			r=min(m/(m/l),K/(K/l)),
			(sumx+=(getg(r,con[x])-getg(l-1,con[x]))%M*getf(m/l,con[x])%M*getf(K/l,con[x])%M+M)%=M;
		(sum+=(n/x)*sumx)%=M;
	}
	return sum;
} 
int main() {
	Euler();
//	for(int i=1;i<=10;i++)
//		cout<
	int T;
	cin>>T;
	while(T--) {
		int n,m,K;
		cin>>n>>m>>K;
		cout<<calc(n,m,K)<<endl; 
	}
	return 0;
}

因此考虑递推，先对质因子个数少的$x$统计答案，再根据质因子个数少的$f,g$函数值计算出质因子个数多的$x$的$f,g$函数值，然后再计算答案：

#include
#include
#include
using namespace std;
const int N=1e5;
const long long M=1e9+7;
vector<int> sta;
bool vis[N+5];
int mu[N+5],LPF[N+5],con[N+5],s0[N+5],LPFx[N+5],cnt[N+5];
//莫比乌斯函数，最小质因子，本质相同素数，约数个数，含有的最小质因子的次数，本质不同质因子个数+1 
int now;
long long f[N+5][20],g[N+5][20];
void Euler()