基于堆叠⾃编码器的时间序列预测 深层神经网络

自适应迭代扩展卡尔曼滤波算法（AIEK）是一种滤波算法，其目的是通过迭代过程来逐渐适应不同的状态和环境，从而优化滤波效果。

该算法的基本思路是在每一步迭代过程中，根据所观测的数据和状态方程，对滤波器的参数进行自适应调整，以便更好地拟合实际数据的分布。具体而言，该算法包括以下步骤：

初始化：首先，为滤波器的初始参数设定一个初始值，这些参数包括状态转移矩阵、测量矩阵、过程噪声协方差和测量噪声协方差等。
预测：根据当前的状态方程和滤波器参数，对下一个状态进行预测，并计算预测误差。
校正：根据预测结果和实际观测数据，对预测进行修正，以便更好地拟合实际数据的分布。
参数更新：根据校正结果，自适应地调整滤波器参数，以便在下一个迭代过程中更好地拟合数据。
该算法具有自适应性和迭代性，能够逐渐适应不同的状态和环境，从而优化滤波效果。在实际应用中，可以根据具体问题选择不同的滤波器参数调整方法和迭代策略，以获得更好的滤波效果。

清空环境变量

warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

导入数据(20步滑动窗口已处理过)

x_train = xlsread('P_x_train.xlsx','B2:U5043');
y_train = xlsread('P_y_train.xlsx','B1:B5042');
x_test = xlsread('P_x_test.xlsx','B2:U1720');
y_test = xlsread('P_y_test.xlsx','B1:B1719');

数据归一化

[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

转置以适应模型

p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';

建立深层神经网络

hidden   = [f_, 50, 50];                     % 自动编码器的隐藏层节点个数[50, 50]
sae_lr   = 0.5;                              % 自动编码器的学习率
sae_mark = 0;                                % 自动编码器的噪声覆盖率（不为零时，为堆叠去噪自动编码器）
sae_act  = 'sigm';                           % 自动编码器的激活函数

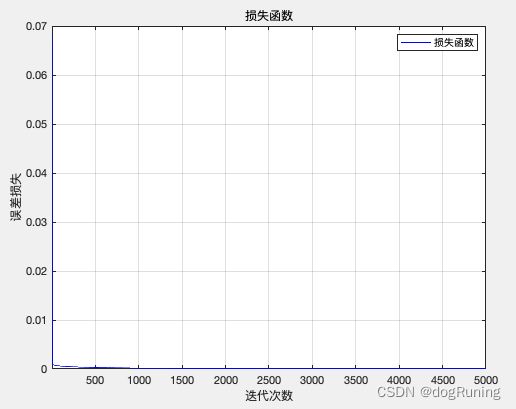
opts.numepochs = 500;                        % 自动编码器的最大训练次数
opts.batchsize = M / 2;                      % 每次训练样本个数 需满足：（M / batchsize = 整数）

%%  建立堆叠自编码器
sae = saesetup(hidden);

%%  堆叠自动编码器参数设置
for i = 1 : length(hidden) - 1
    sae.ae{i}.activation_function     = sae_act;    % 激活函数
    sae.ae{i}.learningRate            = sae_lr;     % 学习率
    sae.ae{i}.inputZeroMaskedFraction = sae_mark;   % 噪声覆盖率
end

%%  训练堆叠自动编码器
sae = saetrain(sae, p_train, opts);

%%  建立深层神经网络
nn = nnsetup([hidden, outdim]);

相关指标计算

%  R2
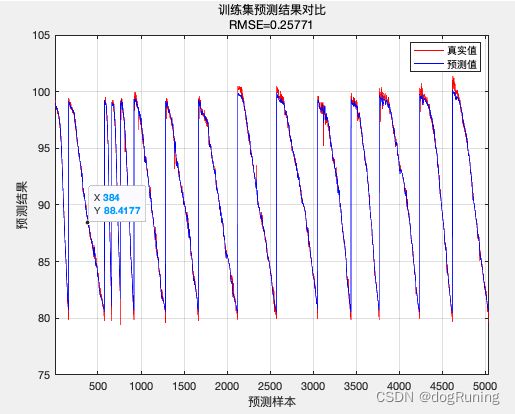
R1 = 1 - norm(T_train - T_sim1')^2 / norm(T_train - mean(T_train))^2;
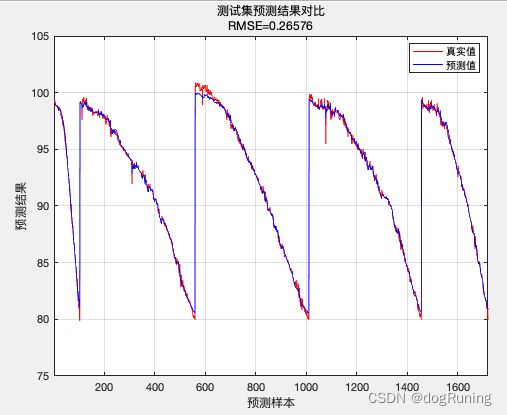
R2 = 1 - norm(T_test  - T_sim2')^2 / norm(T_test  - mean(T_test ))^2;

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

%  MAE
mae1 = sum(abs(T_sim1' - T_train)) ./ M ;
mae2 = sum(abs(T_sim2' - T_test )) ./ N ;

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])

%  MBE
mbe1 = sum(T_sim1' - T_train) ./ M ;
mbe2 = sum(T_sim2' - T_test ) ./ N ;

disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])