【transformer】动手学ViT

ICLR2021

一幅图像值16x16个字：用于图像识别的transformers
将纯Transformer结构运用在CV中

Code

摘要

虽然Transformer架构已经成为NLP标准，但它在CV上的应用仍然有限。在CV中，attention要么与卷积网络一起应用，要么用于替换卷积网络的某些组件，同时保持其整体结构不变。作者认为这种对CNN的依赖是不必要的，直接应用于图像patch序列的纯transformer可以在图像分类任务上表现得非常好。当对大量数据进行预训练并传输到多个中型或小型图像识别基准(ImageNet, CIFAR-100, VTAB等)时，Vision Transformer (ViT)与最先进的卷积网络相比获得了出色的结果，同时需要更少的计算资源来训练。

Method

在模型设计上尽可能遵循原来的Transformer^[1]，对整个图像分类流程进行最少的修改，可扩展性强，以至于启发了后续大量的相关研究。

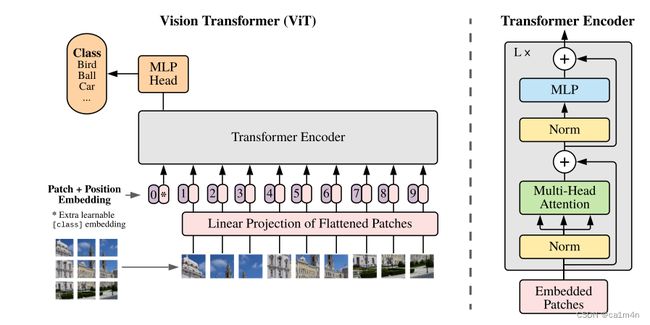
patch0是一个整合信息的可学习向量，用来对该图像进行分类，我们通常将人为增加的这个向量称为 Class Token。【因为原始输出的1-9向量单用都不合适，全用计算量又太大】
图像切分重排之后就失去了位置信息，所以需要加上位置信息（positional embedding）重新传进网络。【注意位置编码的操作是sum，而不是concat】

# 构造patch0
cls_tokens = repeat(self.cls_token, '() n d ->b n d', b = b)
x = torch.cat((cls_tokens, x), dim = 1)
# positional embedding
x += self.pos_embedding[:, :(n+1)]
x = self.dropout(x)

标准Transformer接收的输入是token embedding的1维序列，而对于2维的图像输入，我们将其reshape为平面2维的patch。
Transformer使用大小为D的常数向量在所有层中传递，所以我们拉平图像块，使用可训练的线性投影映射到D维。我们把这个投影的输出称为patch embeddings。
图像切分重排

self.to_patch_embedding = nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1 = patch_height, p2 = patch_width), #图片切分重排
            nn.Linear(patch_dim, dim), # Linear Projection of Flattened Patches
        )

主要结构：

• Transformer的编码器由交替的多头自注意力（MSA）与多层感知机（MLP）模块组成。

x = self.transformer(x)

class Transformer(nn.Module):
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout = 0.):
        super().__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                PreNorm(dim, Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout)),
                PreNorm(dim, FeedForward(dim, mlp_dim, dropout = dropout))
            ]))
    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x
        return x

• Linear Projection of Flattened Patches（embedding层），线性操作降维到D。

nn.Linear(patch_dim, dim) # patch_dim = channels * patch_height * patch_width

• ViT中使用了 MLP Head对输出进行分类处理，这里的 MLP Head 由 LayerNorm 和两层全连接层组成，并且采用了 GELU 激活函数。

# layer norm
class PreNorm(nn.Module):
	def __init__(self, dim, fn):
		super().__init__()
		self.norm = nn.LayerNorm(dim)
		self.fn = fn
	def forward(self, x, **kwargs):
		return self.fn(self.norm(x), **kwargs)
# 一层FC，然后gelu，再FC层
class FeedForward(nn.Module):
	def __init__(self, dim, hidden_dim, dropout = 0.):
		super().__init__()
		self.net = nn.Sequential(
			nn.Linear(dim, hidden_dim),
			nn.GELU(),
			nn.Dropout(dropout),
			nn.Linear(hidden_dim, dim),
			nn.Dropout(dropout)
		)
	def forward(self, x):
		return self.net(x)

实验

ViT模型变体的细节设置

使用大规模数据集预训练后的 ViT 算法，迁移到其他小规模数据集进行训练，与使用 CNN 结构的SOTA算法精度对比

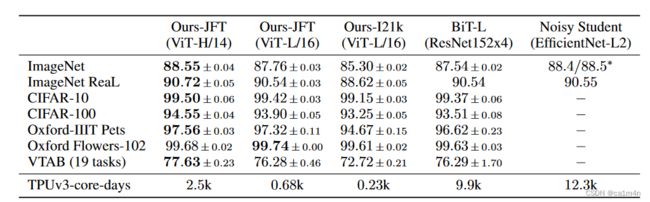
代码-基于pytorch

vit-pytorch
不是原论文提供的代码
131行

import torch
from torch import nn, einsum
import torch.nn.functional as F

from einops import rearrange, repeat
from einops.layers.torch import Rearrange

# helpers
#如果输入不是个tuple就返回一个tuple
def pair(t):
    return t if isinstance(t, tuple) else (t, t)

# classes
#layer norm
class PreNorm(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.norm = nn.LayerNorm(dim)
        self.fn = fn
    def forward(self, x, **kwargs):
        return self.fn(self.norm(x), **kwargs)
#fc层，过一层fc，然后gelu，然后再fc
class FeedForward(nn.Module):
    def __init__(self, dim, hidden_dim, dropout = 0.):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim, dim),
            nn.Dropout(dropout)
        )
    def forward(self, x):
        return self.net(x)
#attention实现
class Attention(nn.Module):
    def __init__(self, dim, heads = 8, dim_head = 64, dropout = 0.):
        super().__init__()
        inner_dim = dim_head *  heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.attend = nn.Softmax(dim = -1)
        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

    def forward(self, x):
        b, n, _, h = *x.shape, self.heads
        #得到qkv
        qkv = self.to_qkv(x).chunk(3, dim = -1)
        #切分qkv
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = h), qkv)
        #dot product后除以根号下norm
        dots = einsum('b h i d, b h j d -> b h i j', q, k) * self.scale
        #softmax
        attn = self.attend(dots)
        #乘到v上，再sum，得到z
        out = einsum('b h i j, b h j d -> b h i d', attn, v)
        #整理shape输出
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)
#transformer block，分成了attention实现和fc实现两部分
class Transformer(nn.Module):
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout = 0.):
        super().__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                PreNorm(dim, Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout)),
                PreNorm(dim, FeedForward(dim, mlp_dim, dropout = dropout))
            ]))
    def forward(self, x):
        #内部主要负责实现block的前向部分。
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x
        return x

class ViT(nn.Module):
    def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool = 'cls', channels = 3, dim_head = 64, dropout = 0., emb_dropout = 0.):
        super().__init__()
        image_height, image_width = pair(image_size)
        patch_height, patch_width = pair(patch_size)

        assert image_height % patch_height == 0 and image_width % patch_width == 0, 'Image dimensions must be divisible by the patch size.'

        num_patches = (image_height // patch_height) * (image_width // patch_width)
        patch_dim = channels * patch_height * patch_width
        assert pool in {'cls', 'mean'}, 'pool type must be either cls (cls token) or mean (mean pooling)'

        self.to_patch_embedding = nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1 = patch_height, p2 = patch_width),
            nn.Linear(patch_dim, dim),
        )

        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim))
        self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
        self.dropout = nn.Dropout(emb_dropout)

        self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)

        self.pool = pool
        self.to_latent = nn.Identity()

        self.mlp_head = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, num_classes)
        )

    def forward(self, img):
        #输入端适配
        x = self.to_patch_embedding(img)
        b, n, _ = x.shape
        #引入patch 0
        cls_tokens = repeat(self.cls_token, '() n d -> b n d', b = b)
        x = torch.cat((cls_tokens, x), dim=1)
        #positional embedding
        x += self.pos_embedding[:, :(n + 1)]
        x = self.dropout(x)
        #Transformer前向
        x = self.transformer(x)
        #拿到最后输入进mlp的patch
        x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0]
        x = self.to_latent(x)
        return self.mlp_head(x)

Training Visual Transformer on Dogs vs Cats Data

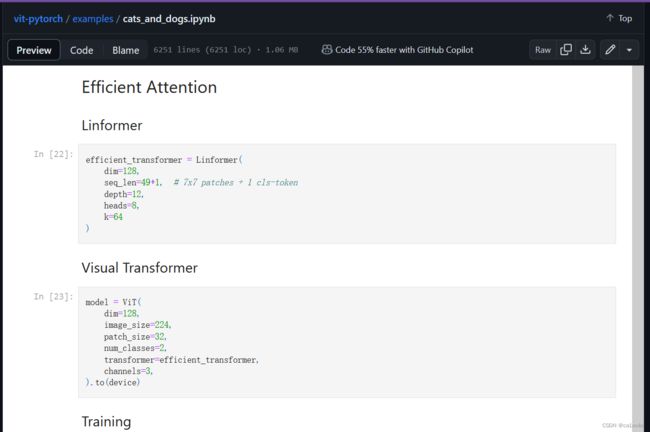
线性注意力（linear attention）机制将序列划分成固定大小的块，并仅对每个块内的元素进行注意力计算，而不是全局计算。通过将线性注意力引入传统的Transformer模型，Linformer能够更有效地处理长序列数据。

注释

[1] Ashish Vaswani.Attention is all you need,NIPS,2017
[2] 基于paddlepaddle2.1 | 深入理解图像分类中的Transformer-Vit,DeiT
[3] ViT猫狗大战示例

---

一些词汇

saturating performance 饱和性能
unprecedented 空前的
substantially 本质上；大体上
de-facto 事实上的
scalability 可扩展性