二维差分---基础算法

书接上回

a二维数组是b二维数组的前缀和数组,b二维数组是a二维数组的差分数组,也就是说a[i][j]=b[1][1]+b[1][2] + ......b[i][1] + b[i][2] + ...... b[i][j] ,下图是b的二维数组

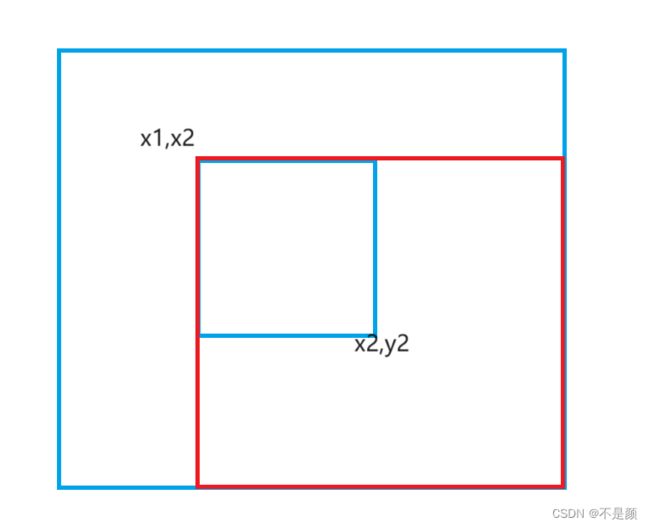
如图,当你想要整个矩阵中的一个子矩阵都加上一个C,如果我们将b[x1][x2]加上C,那么a数组右下角所有的区域都会加上C,可是我们只想其中的子矩阵加上C,那么如何解决呢?照猫画虎就行,如下图

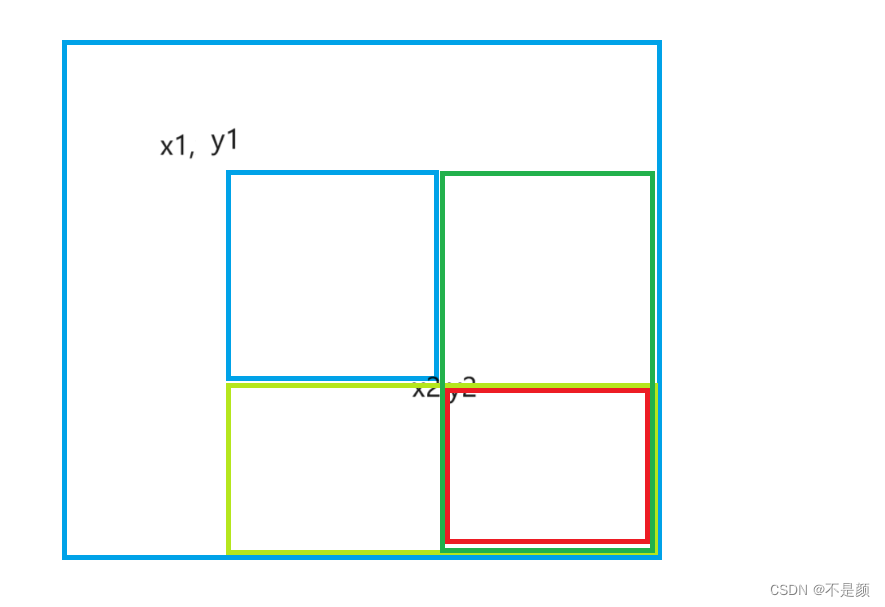
b[x2+1][y2]减去C,那么图中青绿色的区域都会减去C,b[x1][y1+1]减去C,那么图中绿色区域都会减去C,很明显这样的操作会对红色区域减去两个C,所以b[x2+1][y2+1]加上C,那么红色区域都会加上C

所以就是

b[x1][x2]+=C

b[x2+1][y2]-=C

b[x1][y1+1]-=C

b[x2+1][y2+1]+=C

很好,根据上一篇文章,可以很容易得到插入函数

题目

题目描述
输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

输入样例
 

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例
 

2 3 4 1
4 3 4 1
2 2 2 2

代码

#include 

using namespace std;

const int N = 1010;
int b[N][N];
int a[N][N];

int n, m, q;


void insert(int x1, int y1, int x2, int y2, int c)
{

	b[x1][y1] += c;

	b[x2 + 1][y1] -= c;

	b[x1][y2 + 1] -= c;

	b[x2 + 1][y2 + 1] += c;

}
int main(void)
{
	scanf("%d%d%d", &n, &m, &q);

	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			scanf("%d", &a[i][j]);
			insert(i, j,i,j, a[i][j]);
		}
	}


	while (q--)
	{
		int x1, y1, x2, y2, c;
		scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
		insert(x1, y1, x2, y2, c);
	}

	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
			printf("%d ", b[i][j]);
		}
		printf("\n");
	}
	

	return 0;
}