数据结构——二叉树
堆的简易建立
- 前言
- 堆的顺序表实现
-
- 一、Heap.h头文件
-
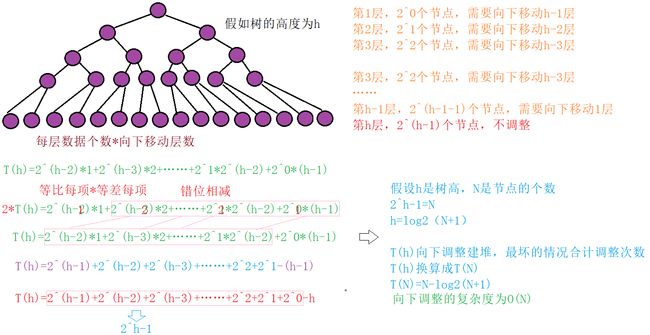
- 向下调整算法复杂度
- 向上调整算法复杂度
- 二、Heap.c功能函数文件
- 三、Test.c测试函数文件
- 四、运行结果展示
- 五、完整代码展示
- 二叉树的链表实现
-
- 回顾二叉树的概念
- 链式二叉树代码模拟
- 二叉树的遍历
- 总结
前言
现在我们开始学习堆的建立!
相对于以前学的数据结构,堆无疑是更为复杂的!
但没关系,一起加油,这些都是小困难!芜湖~
在前面我们对于堆这个概念有了大概的认知;
现在我们来用代码实现一下吧!
堆的顺序表实现
我们用大根堆来进行代码实现!
一、Heap.h头文件
- 头文件的声明
#pragma once
#include
- 堆的接口实现
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}HP;
前面的文章提到了堆的顺序表存储结构!
如果不了解可以看看之前的文章!
文章链接

- 向上调整和向下调整函数声明
//向上调整
void AdjustUp(HPDataType* a, int child);
//向下调整
void AdjustDown(HPDataType* a, int n, int parent);
前文对于两种调整方法同样也给出了详细的讲解!
不了解的可以先看看前面的文章!
文章链接
向下调整算法复杂度
向上调整算法复杂度
- 初始化堆和顺序表以及打印销毁函数的声明
//打印堆
void HeapPrint(HP* php);
//初始化堆
void HeapInit(HP* php);
//初始化顺序表
void HeapInitArray(HP* php, int* a, int n);
//销毁
void HeapDestroy(HP* php);
- 交换结点以及判空函数的声明
//交换结点内容
void Swap(HPDataType* p1, HPDataType* p2);
//判空
bool HeapEmpty(HP* php);
- 插入删除以及找出堆顶元素函数的声明
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//堆顶元素
HPDataType HeapTop(HP* php);
二、Heap.c功能函数文件
- 头文件的声明
#include "Heap.h"
- 向上调整和向下调整函数的定义
//向上调整
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}
//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// 找出大的那个孩子
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
// 继续往下调整
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
- 初始化堆和顺序表以及打印销毁函数的定义
//初始化堆
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;//长度
php->capacity = 0;//容量
}
//初始化顺序表
void HeapInitArray(HP* php, int* a, int n)
{
assert(php);
assert(a);
php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (php->a == NULL)
{
perror("malloc fail");
exit(-1);
}
php->size = n;
php->capacity = n;
memcpy(php->a, a, sizeof(HPDataType) * n);//将数组a中的数据复制到存储堆的顺序表中
// 建堆
for (int i = 1; i < n; i++)
{
AdjustUp(php->a, i);//将顺序表中的数据依次向上调整
}
}
//打印
void HeapPrint(HP* php)
{
assert(php);
for (size_t i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
//销毁
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = php->capacity = 0;
}
- 交换结点以及判空函数的定义
//交换结点内容
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//判空
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
- 插入删除以及找出堆顶元素函数的定义
//插入
void HeapPush(HP* php, HPDataType x)
{
assert(php);
// 扩容
if (php->size == php->capacity)
{
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
php->a = tmp;
php->capacity = newCapacity;
}
php->a[php->size] = x;
php->size++;
AdjustUp(php->a, php->size - 1);
}
//删除
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&php->a[0], &php->a[php->size - 1]);
--php->size;
AdjustDown(php->a, php->size, 0);
}
//堆顶
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
三、Test.c测试函数文件
1.排序函数的定义
// 升序
void HeapSort(int* a, int n)
{
// 建堆 (大堆)or (小堆)
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
2.主函数的定义
int main() {
int a[] = { 2,3,5,7,4,6,8 };
HP hp;
HeapInit(&hp);
HeapSort(a, sizeof(a) / sizeof(int));
HeapInitArray(&hp, a, sizeof(a) / sizeof(a[0]));
HeapPush(&hp,9);//插入9
HeapPush(&hp, 10);//插入10
HeapPop(&hp);//删除10
HeapPrint(&hp);
HeapDestroy(&hp);
return 0;
}
四、运行结果展示
五、完整代码展示
1.Heap.h头文件
#pragma once
#include2.Heap.c头文件
#include "Heap.h"
//初始化堆
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
//初始化顺序表
void HeapInitArray(HP* php, int* a, int n)
{
assert(php);
assert(a);
php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (php->a == NULL)
{
perror("malloc fail");
exit(-1);
}
php->size = n;
php->capacity = n;
memcpy(php->a, a, sizeof(HPDataType) * n);
// 建堆
for (int i = 1; i < n; i++)
{
AdjustUp(php->a, i);
}
}
//销毁
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = php->capacity = 0;
}
//交换结点内容
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//向上调整
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}
//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
// 继续往下调整
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//插入
void HeapPush(HP* php, HPDataType x)
{
assert(php);
// 扩容
if (php->size == php->capacity)
{
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
php->a = tmp;
php->capacity = newCapacity;
}
php->a[php->size] = x;
php->size++;
AdjustUp(php->a, php->size - 1);
}
//打印
void HeapPrint(HP* php)
{
assert(php);
for (size_t i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
//删除
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&php->a[0], &php->a[php->size - 1]);
--php->size;
AdjustDown(php->a, php->size, 0);
}
//堆顶
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
//判空
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
3.Test.c头文件
#include"Heap.h"
// 升序
void HeapSort(int* a, int n)
{
// 建堆 (大堆)or (小堆)
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
int main() {
int a[] = { 2,3,5,7,4,6,8 };
HP hp;
HeapInit(&hp);
HeapSort(a, sizeof(a) / sizeof(int));
HeapInitArray(&hp, a, sizeof(a) / sizeof(a[0]));
HeapPush(&hp,9);
HeapPush(&hp, 10);
HeapPop(&hp);
HeapPrint(&hp);
HeapDestroy(&hp);
return 0;
}
二叉树的链表实现
回顾二叉树的概念
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的
链式二叉树代码模拟
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->_left = node2;
node1->_right = node4;
node2->_left = node3;
node4->_left = node5;
node4->_right = node6;
return node1;
}
当然,这只是一个形象模拟,二叉树真正的创建过程不是这样的哦!
二叉树的遍历
前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。
遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);


现在我们已经对于链式二叉树有了基本的了解啦!
后面我会带来一些链式二叉树的题型!
请持续关注!!!
总结
只要一直在学习!
那我们就一直在路上!
终点未知,但努力终有回声!