【数据结构】堆的创建

个人主页 ：阿然成长日记 点击可跳转
个人专栏： 数据结构与算法C语言进阶
不能则学，不知则问，耻于问人，决无长进

前言：

在上一篇博客中，主要讲到了关于堆的各种操作。那么本篇博客将会讲讲我们通过堆可以实现的一些作用-----如堆排序。

一、基于大堆的上下调整

上一篇博客中的上下调整，都是以调成小堆为目标。那怎样才能实现调成大堆呢？

1.向上调整

(1)解决措施：

只需要修改比较符>;改为a[parent]<a[child],即可

(2)代码实现

//向上调整
void AdjustUp(HPDataType* a, int child)
{
	//传入数组，child为孩子节点下标
	int parent = (child - 1) / 2;
	//当一直交换到根，停止
	while (child>0)
	{
		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			return;
	}
}

(3)测试

输入数组：int a[] = { 2,4,5,3,1,9 };

2.向下调整

(1)解决措施：

只需要修改比较符 <改为child + 1 < n && a[child + 1] > a[child],
因为建大堆，需要找大的那个进行交换。

(2)代码实现

//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	//一直交换到数的最后，也就是数组的最后一个位置
	while (parent<n)
	{
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			// 继续往下调整
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			return;
		}
	}
}

3.总结

-	大堆	小堆
向上调整	parent>child	parent
向下调整	比较两个孩子，选择大的进行比较交换	选择小的进行比较交换

二、创建堆

两种方法建堆均以建立小堆为目标。无论是创建小堆还是创建大堆，思路都一样，通过修改Adjust方法即可

建堆【方法一】使用向上调整

创建堆的思路可以通过向上调整，也可通过向下调整。这里讲通过向上调整建立堆.<从上到下>

由于我的AdjustUp函数是用来调整大堆的，所以，这里创建的也是大堆。

1.思路

传入参数
a：数组，n：是数组元素个数
1.为p->a开辟n个空间；
2.利用memcpy函数，把数组a复制到p->a中
3.在使用AdjustUp调整，从1-n-1逐步向下延伸；

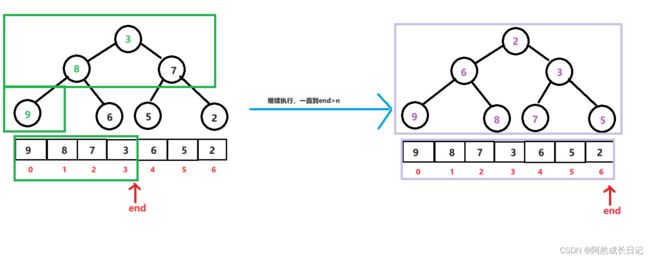
2.代码实现

//建立大堆
void HeapInitArray(HP* p, int* a, int n)
{
	//a：数组，n：是数组元素个数
	assert(p);
	assert(a);

	p->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (p->a == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	p->size = n;
	p->capacity = n;
	//把传入数组a复制到p->a中
	memcpy(p->a, a, sizeof(HPDataType) * n);

	// 向上调整，调整成一个小堆
	for (int i = 1; i < n; i++)
	{
		AdjustUp(p->a, i);
	}
}

建堆【方法二】使用向下调整

这里通过向下调整建立堆.<从下到上>

1.思路：

1.从倒数第一个非叶子节点开始向下调整，因为叶子节点没有左右子树。
2.根据Adjust方法，比较交换。
3.层层向上，下层可以保证是堆。从而可保证向下调整的进行。
所以，我们说这种调整方式是从下到上的。
步骤图：

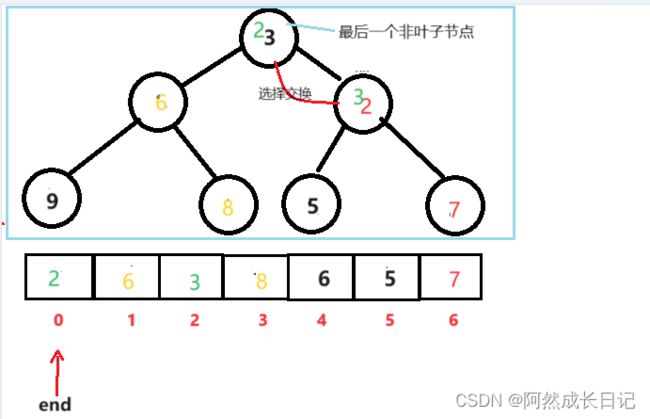
三、堆排序

排升序【方法一:向上】

口诀：排升序，建大堆

意思是：想要将数组的顺序变成一个升序的，那么可以建立一个大堆存在数组中，在对堆进行调整。即可将数组变成一个升序数组。

1.思路：

首先建立大堆；
1.堆顶与最后一个节点交换，由于是大堆，堆顶是最大值。交换后，就选出了最大值并将其放到数组的组后位置，
2.并将堆的长度减1（数组长度减1）。
3.在对剩下的堆进行向下调整，从而将第二大的数调整到了堆顶。此步骤时间复杂度：O(logN)
4.最后，这个原本存储大堆的数组，就变成了一个从小到大的升序数组。

2.代码实现：

//排升序
void HeapSortASC(int* a, int n)
{
	//建立大堆
	for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		swap(&a[0], &a[end]);
		//每次调整从根0到end，end每次会减1。
		AdjustDown(a, end, 0);
		end--;
	}
}

3.时间复杂度分析

一次AdjustUp调整的时间复杂度是O(logN)。
一共执行n-1次，所以，时间复杂度一共是O(N*logN)。

排降序

口诀：排降序，建小堆

1.思路：

首先建立小堆；
1.堆顶与最后一个节点交换，由于是小堆，堆顶是最小值。交换后，就选出了最小值并将其放到数组的组后位置，
2.并将堆的长度减1（数组长度减1）。
3.在对剩下的堆进行向下调整，从而将第二大的数调整到了堆顶。此步骤时间复杂度：O(logN)
4.最后，这个原本存储大堆的数组，就变成了一个从小到大的升序数组。

2.代码实现：

修改AdjustUp(a, i);和AdjustDown(a, end, 0);为调小堆

void HeapSortDES(int* a, int n)
{
	//建立小堆
	for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		//每次调整从根0到end，end每次会减1。
		AdjustDown(a, end, 0);
		--end;
	}
}

3.时间复杂度分析

一次AdjustUp调整的时间复杂度是O(logN)。
一共执行n-1次，所以，时间复杂度一共是O(N*logN)。