RSA算法原理与实现(课程设计)
引言
现在社会已经进入信息时代,网络技术全球化的发展已经完全改变了人们传递信息的方式和方法。Internet技术已经进入到人们生活中的方方面面,成为信息交流的重要手段。这些技术给我们的生活和工作带来极大便利的同时,也给我们带来了新的挑战,要求网络的更高安全性成为了我们关注的焦点.因此如何保护网络信息传输的安全成为各大科研机构的重大课题。
RSA密码系统是较早提出的一种公开钥密码系统。1978年,美国麻自理工学院(MIT)的Rivest,Shamir和Adleman在题为“获得数字签名和公开钥密码系统的方法”的论文中提出了基于数论的非对称(公开钥)密码体制,称为RSA密码体制。RSA是建立在“大整数的素因子分解是困难问题”基础上的,是一种分组密码体制。
RSA算法是一种公钥密码体制,是目前使用最为广泛的一种密码体制,但由于RSA算法是基于大素数分解难题的,所以为了防止各种各样的攻击,其模长在不断增长,RSA算法的大部分运算都是大整数的模幂和模乘,所以其运行速度较慢成为RSA的一个显著特点。另外随着各种攻击手段的增多,RSA在安全性上也受到了很大的冲击。RSA密码体制在理论上是非常安全的,但是由于在实际应用中,具体的RSA密码系统都不一样的,每一个系统的设计都有着自己的具体要求,或者是对速度的要求,或者是对安全性的要求。
本次课程设计所设计的RSA密码算法能够实现以下基本任务:
- 能够随机生成两个大的质数(素数)p和q。
- 能够对生成的两个大的素数进行判断,并能计算出阈值,即t=(q-1)*(p-1)=?。
- 可将所有符合e与t互质,e的选取全部输出,从中任选出一个,即为公钥,然后生成公钥d,使d*emod t=1, 最后丢弃p,q,t,则公钥为e,私钥为d。
- 能够读取文本文件,对文件中的数据进行加密。
- 可对加密后的数据进行解密。
课程设计目的:在充分理解RSA加密体制概念和原理的基础上,用 Dev-C++ 实现 RSA 加密与解密,演示公钥与密钥的生成及加密与解密的过程,进一步熟悉C语言或其他程序设计语言。
开发环境及工具:
硬件:运行Windows操作系统的计算机
软件:Dev-c++
开发语言:C++
关键词:Mod运算;Miller-Rabin素数检测;gcd算法;
目录
1.有关RSA密码算法的基本知识... 4
1.1素数. 4
1.2模运算. 4
1.3欧拉函数和欧拉定理. 5
1.4欧几里德算法. 5
2.RSA算法设计... 5
2.1算法描述. 5
2.2 RSA算法流程图. 8
3.基于C++的RSA密码算法的核心代码... 10
3.1 C++语言的优势与特点. 10
3.2 RSA密码算法的核心代码. 10
4.RSA公钥密码方案... 14
4.1公钥密码系统的应用. 14
4.2使用公钥密码方案优点. 15
4.3使用公钥密码方案缺点. 16
4.4 RSA的安全性分析. 16
5.RSA密码算法的实现效果... 16
课程设计心得体会. 18
参考文献. 19
RSA密码算法的设计与实现
1.有关RSA密码算法的基本知识
1.1素数
称整数p(p>1)是素数,如果p的因子只有±1,±p。
称c是两个整数a、b的最大公因子,如果 :
① c 是 a 的因子也是b的因子,即c是 a、b 的公因子。
② a 和 b 的任一公因子,也是c的因子。
表示为 c=gcd(a, b)。
由于要求最大公因子为正,所 以 gcd(a,b)=gcd(a,-b)=gcd(-a,b)=gcd(-a,-b。) 一 般 gcd(a,b)=gcd(|a|,|b|)。由任一非0整数能整除0,可得 gcd(a,0)=|a|。如果将 a,b 都表示 为素数的乘积,则 gcd(a, b)极易确定。 一般由 c=gcd(a,b)可得:对每一素数 p,cp=min(ap,bp)。由于确定大数的素因子不很容易,所以这种方法不能直接用于求两个大数的最大公因子,如何求两个大数的最大公因子在下面介绍。
如果 gcd(a,b)=1,则称a和b互素。
1.2模运算
设n是一正整数,a是整数,如果用n除a,得商为q,余数为r,则 a=qn+r,0≤r
1.3欧拉函数和欧拉定理
欧拉函数:设n是一正整数,小于n且与n互素的正整数的个数称为 n 的欧拉函数,记为φ(n)。
若n是素数,则显然有φ(n)=n-1。
若n是两个素数p和q的乘积,则φ(n)=φ(p)×φ(q)=(p-1)×(q-1)。
欧拉定理:若a和n互素,则 aφ(n)≡1 mod n。
1.4欧几里德算法
欧几里得(Euclid)算法是数论中的一个基本技术,是求两个正整数的最大公因子的简化过程。而推广的 Euclid 算法不仅可求两个正整数的最大公因子,而且当两个正整数互素时,还可求出其中一个数关于另一个数的乘法逆元。
1. 求最大公因子: Euclid算法是基于下面一个基本结论: 对任意非负整数 a 和正整数 b,有 gcd(a, b)=gcd(b, a mod b。)
2. 求乘法逆元: 如果 gcd(a, b)=1 ,则 b 在 mod a下有乘法逆元(不妨设 b
2.RSA算法设计
2.1算法描述
RSA 算法描述:
- 密钥的产生
① 选两个保密的大素数 p 和 q。
② 计算 n=p×q,φ(n)=(p-1)(q-1)其, 中 φ(n)是 n 的欧拉函数值。
③ 选一整数 e,满足 1 ,且 gcd(φ(n),e)=1。
④ 计算 d,满足 d·e≡1 mod φ(n),即 d 是 e 在模 φ(n)下的乘法逆元,因 e 与 φ(n)互素, 由模运算可知,它的乘法逆元一定存在。
⑤ 以{e,n}为公开钥,{d,n}为秘密钥。
- 加密
加密时首先将明文比特串分组,使得每个分组对应的十进制数小于 n,即分组长度小于 log2n。然后对每个明文分组 m,作加密运算: c≡me mod n
- 解密 对密文分组的解密运算为: m≡cd mod n
下面证明 RSA 算法中解密过程的正确性。
证明: 由加密过程知 c≡me mod n,所以 cd mod n≡med mod n≡m1 mod φ(n) mod n≡mkφ(n)+1 mod n
要获得两个随机的小于 100 的素数,可以首先将系统当前时间设置为随机数种子, 然后对生成的随机数取 100 模,然后调用判断素数的函数。要判断一个属实否为素数, 可以判断数 n 从 2 到 n 的开方,是否能整除 n。伪代码如下:
for(i从 2 到 n 的开方 ; i++) {
if(n被 i 整除)
则 n 不是素数终止循环;
if(i > n的开方 ) 返回 n 为宿素数;
}
(4)求最大公因子和求乘法逆元函数:
bool gcd(int p,int q){
int temp1,temp2; //q=temp2*p+temp1 ;
if(q
temp1=p;
p=q;
q=temp1;
}
temp1=q%p,temp2=q/p;
while(temp1!=0){
q=p;p=temp1;
temp1=q%p;temp2=q/p;
}
if(temp1==0&&temp2==q){
printf("符合条件!\n");
return true;
}
else{
printf("不符合条件!请重新输入:\n");
return false;
}
}
2.2 RSA算法流程图
1.继承自C语言的优点:语言简洁、紧凑,使用方便、灵活;拥有丰富的运算符;生成的目标代码质量高,程序执行效率高;可移植性好等。
3.基于C++的RSA密码算法的核心代码
3.1 C++语言的优势与特点
C++语言是在C语言的基础上发展而来,同时它又支持面向对象的程序设计,它主要具有以下特点:
2.对C语言进行的改进:编译器更加严格,引入引用的概念,引入const常量和内联函数,取代宏定义等。
3.同时支持面向过程和面向对象的方法:在C++环境下既可以进行面向对象的程序设计,也可以进行面向过程的程序设计。因此它也具有数据封装和隐藏、继承和多态等面向对象的特征。
C++语言既保留了C语言的有效性、灵活性、便于移植等全部精华和特点,又添加了面向对象编程的支持,具有强大的编程功能,可方便地构造出模拟现实问题的实体和操作;编写出的程序具有结构清晰、易于扩充等优良特性,适合于各种应用软件、系统软件的程序设计。用C++编写的程序可读性好,生成的代码质量高,运行效率仅比汇编语言慢10%~20%。
3.2 RSA密码算法的核心代码
//判断两个数是不是互素(见 2.1(4))
//求e关于模(p-1)(q-1)的逆元d:即私钥
int extend(int e,int t){
int d;
for(d=0;d
if(e*d%t==1)
return d;
}
}
//判断输入的p和q是不是素数
bool is_sushu(int s){
for(int i=2;i
if(s%i==0) return false;
}
return true;
}
//加密函数
void encrypt(int e,int n,char mingwen[100]){ //自己指定指数e
//先将符号明文转换成字母所对应的ascii码。
//char mingwen[100]; //符号明文
changdu=strlen(mingwen);
int ming[strlen(mingwen)]; //定义符号明文
for(int i=0;i
ming[i]=mingwen[i]; //将字母转换成对应的ascii码。
printf("%d",mingwen[i]); //将字母转换成对应的ascii码。可以不打印
}
printf("\n");
//开始加密
printf("加密开始…………………………\n");
int zhuan=1; //c为加密后的数字密文
for(int i=0;i
for(int j=0;j
zhuan=zhuan*ming[i]%n;
//zhuan=zhuan%n;
}
c[i]=zhuan;
//printf("%d",mi[i]);
zhuan=1;
}
printf("加密密文为:\n");
for(int i=0;i
printf("%d",c[i]);
printf("\n加密结束…………………………\n");
}
//解密函数
void decrypto(int d,int n){
int de_mingwen[changdu],zhuan1=1;
char de_ming[changdu];
for(int i=0;i
for(int j=0;j
zhuan1=zhuan1*c[i]%n;
}
de_mingwen[i]=zhuan1;
zhuan1=1;
}
printf("解密开始…………………………\n");
printf("解密后的数字明文为:\n");
for(int i=0;i
printf("%d",de_mingwen[i]);
printf("\n");
printf("解密后的符号明文为:\n");
for(int i=0;i
de_ming[i]=de_mingwen[i];
printf("%c",de_ming[i]);
}
printf("\n解密结束…………………………\n");
}
//用于读取文件的部分代码
char path[]="text.txt";
FILE *create;
if((create=fopen(path,"r"))!=NULL)
{
int j; char **a;
a=(char **)malloc(100*sizeof(char*)); //此处如果只申请一个char *大小的空间时,
//你以后的a[j]往哪里放?此处的100是假设你的文件中有100行信息。如果超过100还得多分配
for (j=0;;j++)
{
a[j]=(char *)malloc(10000*sizeof(char)); //此处只申请一个字符的空间,后面读取
//长度为10000的字符串就没地方存放了
fgets(a[j],10000,create);
printf("%s",a[j]); //测试读取是否成功,将文件中信息显示到屏幕上
if(feof(create)!=0)
{
for(;j=0;j--)
free(a[j]);
break;
}
}
free(a);
}
else
printf("Fail to open the file.\n");
fclose(create);
printf("\n");
4.RSA公钥密码方案
4.1公钥密码系统的应用
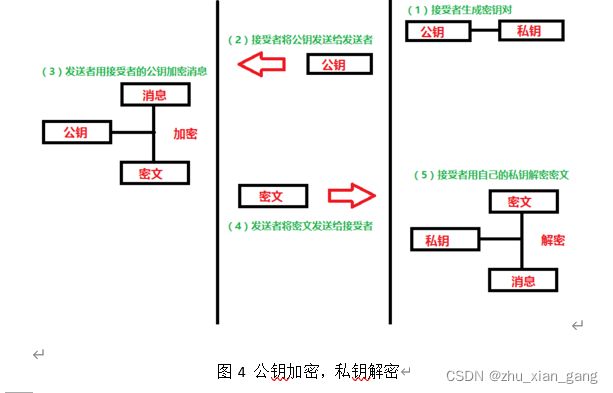
(1)公钥加密,私钥解密
(2)数字签名和数字证书
比如有两个用户Alice和Bob,Alice想把一段明文通过双钥加密的技术发送给Bob,Bob有一对公钥和私钥,那么加密解密的过程如下:
- Bob将他的公开密钥传送给Alice。
- Alice用Bob的公开密钥加密她的消息,然后传送给Bob。
- Bob用他的私人密钥解密Alice的消息。
上面的过程可以用下图表示,Alice使用Bob的公钥进行加密,Bob用自己的私钥进行解密。
4.2使用公钥密码方案优点
(1)保密性方面,我要给你传递个信息,不管是个对称密钥也好其他任意信息也好,我都能采用你公钥开加密,然后再发给你,其原理保证了别人只要拿不到你私钥就都解不开,这里的应用主要是密钥的传递。
(2)完整性方面,你发布或者给人传输了个信息,这个信息是需要验证没被其他人改过或者别人要防止你事后抵赖的,这个时候你就得用自己的私钥加密一下,让人能用你的公钥解开。同样由于公钥体系的基本原理,只要用你的公钥能解密就证明了它确实是你发的,并没被篡改。这里的主要应用就是各种数字签名技术,另外,基于数字证书的登陆也是它的体现。
4.3使用公钥密码方案缺点
速度问题,因为公钥密码体制一般的操作都是模指数运算,模指数运算耗费的时间就要比对称密码体制长得多,所以说速度上的限制,导致了公钥密码体制主要的运用在于加密密钥和数字签名。
4.4 RSA的安全性分析
RSA的安全性依赖于大整数的因式分解问题。实际上,人们推测RSA的安全性依赖于大整数的因式分解问题,但谁也没有在数学上证明从c和e计算m需要对n进行因式分解。可以想象可能会有完全不同的方式去分析RSA。然而,如果这种方法能让密码解析员推导出d,则它也可以用作大整数因式分解的新方法。最难以令人置信的是,有些RSA变体已经被证明与因式分解同样困难。甚至从RSA加密的密文中恢复出某些特定的位也与解密整个消息同样困难。另外,对RSA的具体实现存在一些针对协议而不是针对基本算法的攻击方法。
破译RSA的难度至少和大数分解的困难性相当,大数分解即已知p、q求n=pq容易,但由n求p则极为困难。产生两个100位(十进制)的素数并求它们的乘积(用计算机),只需几秒钟,但分解乘得的结果则需要数十亿年。RSA的公钥为(e, n),私钥为(d,p)。由公钥很难得到私钥(未知 t)。n通常选512b、1024b或2048b。
5.RSA密码算法的实现效果
下图(图6)为进行测试的记事本文件,首先在Dev-C++上运行源代码文件,text.txt放在与rsa.cpp同目录下,即相对路径,运行启动,将会展现如下图(图7)随机产生两个大的素数,并判断是否符合条件,并计算出t的值及计算出所有符合条件的e取值即公钥,从中任取一个即可,本测试取值为(19613),系统可自动计算出密钥d=11885,可由计算机进行验证,接着读取记事本中文件内容,展示,并将其转发为对应的ASSIC(495051),进行加密,密文(810331078286),正确输入对应密钥可进行解密,先展示明文的ASSIC,在显示符号明文(123),加密结束。
课程设计心得体会
本次课程设计使我对RSA密码算法,C++语言的使用,及互素等相关知识有了更进一步的理解,通过建立数学函数,并在主函数中进行整合,再次了解RSA算法的加密解密,以及C++语言的使用,加深了课堂上的理论知识,将理论知识赋予实践,建立了RSA密码算法的整体概念。锻炼了我C++语言赋予实践,解决实际问题的能力。
课程设计是将各个学科综合应用实际的体现,此次课程设计,也让我看到了我还有许多的不足,我进程进行的很缓慢,比如对于编程的一些问题,虽然自身的语法没有错误,但是控制台处会抛出异常,或者是一些的连接错误,这也是我学习C++编程太浅的表现,解决这样的问题需要花费大量的时间,并且问题还不一定会得到解决。
这次实验,不仅培养了我独立思考、动手操作的能力,在各种其它能力上也都有了提高。更重要的是,在实验课上,我们学会了很多学习的方法。而这是日后最实用的,真的是受益匪浅。要面对社会的挑战,只有不断的学习、实践,再学习、再实践。这对于我们的将来也有很大的帮助。
同时也让我学习到了,有什么不明白的问题,可以上网查询,网上一般都会有大量的帖子,或者一些比自己编写出来更优的函数,可以帮助到我们。
最后,我会对这次课程设计出现的各种问题在日后,我会加以改正,感谢老师的辅导以及同学的帮助,让我有了一个更好的认识,无论是学习还是生活,生活是实在的,要踏实走路。课程设计时间虽然很短,但我学习了很多的东西,使我眼界打开,感受颇深。
参考文献
[1]安葳鹏,汤永利,刘坤,闫玺玺,叶青.《网络与信息安全》[M].清华大学出版社:北京市,2017.
[EB/OL]. https://blog.csdn.net/aaron_si/article/details/5116506,2016-04-17
[EB/OL].https://blog.csdn.net/weixin_44116874/article/details/109514047?utm_source=app&app_version=4.20.0&utm_source=app,2020-11-05
[EB/OL].https://blog.csdn.net/qq_35116353/article/details/71076180?utm_source=app&app_version=4.20.0&utm_source=app,2017-05-01
[EB/OL].https://blog.csdn.net/DG_666/article/details/80588203?utm_source=app&app_version=4.20.0&utm_source=app,2018-06-05
[EB/OL]. C语言中读取txt文件内容_百度知道,2013-12-22